Difference between revisions of "2020 IMO Problems/Problem 1"
(→Video solution) |
(→solution 1) |
||
| (8 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Problem | + | == Problem == |
| − | The following ratio equalities hold: | + | Consider the convex quadrilateral <math>ABCD</math>. The point <math>P</math> is in the interior of <math>ABCD</math>. The following ratio equalities hold: |
| − | + | <cmath>\angle PAD : \angle PBA : \angle DPA = 1 : 2 : 3 = \angle CBP : \angle BAP : \angle BPC.</cmath> Prove that the following three lines meet in a point: the internal bisectors of angles <math>\angle ADP</math> and <math>\angle PCB</math> and the perpendicular bisector of segment <math>\overline{AB}</math>. | |
| − | Prove that the following three lines meet in a point: the internal bisectors of angles | + | |
| − | + | ==solution 1== | |
| + | |||
| + | Let the perpendicular bisector of <math>AP,BP</math> meet at point <math>O</math>, those two lines meet at <math>AD,BC</math> at <math>N,M</math> respectively. | ||
| + | |||
| + | As the problem states, denote that <math>\angle{PBC}=\alpha, \angle{BAP}=2\alpha, \angle {BPC}=3\alpha</math>. We can express another triple with <math>\beta</math> as well. Since the perpendicular line of <math>BP</math> meets <math>BC</math> at point <math>M</math>, <math>BM=MP, \angle {BPM}=\alpha, \angle {PMC}=2\alpha</math>, which means that points <math>A,P,M,B</math> are concyclic since <math>\angle{PAB}=\angle{PMC}</math> | ||
| + | |||
| + | Similarly, points <math>A,N,P,B</math> are concyclic as well, which means five points <math>A,N,P,M,B</math> are concyclic., <math>ON=OP=OM</math> | ||
| + | |||
| + | Moreover, since <math>\angle{CPM}=\angle{CMP}</math>, <math>CP=CM</math> so the angle bisector if the angle <math>MCP</math> must be the perpendicular line of <math>MP</math>, so as the angle bisector of <math>\angle{ADP}</math>, which means those three lines must be concurrent at the circumcenter of the circle containing five points <math>A,N,P,M,B</math> as desired | ||
| + | |||
| + | ~ bluesoul | ||
| + | ~ edits by Pearl2008 | ||
| + | |||
| + | ==Solution 2 (Three perpendicular bisectors)== | ||
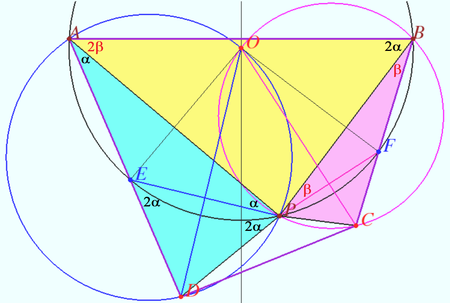
| + | [[File:2020 IMO 1a.png|450px|right]] | ||
| + | The essence of the proof is the replacement of the bisectors of angles by the perpendicular bisectors of the sides of the cyclic pentagon. | ||
| + | |||
| + | Let <math>O</math> be the circumcenter of <math>\triangle ABP, \angle PAD = \alpha, OE</math> is the perpendicular bisector of <math>AP,</math> and point <math>E</math> lies on <math>AD.</math> Then | ||
| + | |||
| + | <cmath>\angle APE = \alpha, \angle PEA = \pi - 2\alpha, \angle ABP = 2\alpha \implies</cmath> | ||
| + | <math>\hspace{33mm} ABPE</math> is cyclic. | ||
| + | <cmath>\angle PED = 2\alpha = \angle DPE \implies</cmath> | ||
| + | the bisector of the <math>\angle ADP</math> is the perpendicular bisector of the side <math>EP</math> of the cyclic <math>ABPE</math> that passes through the center <math>O.</math> | ||
| + | |||
| + | A similar reasoning can be done for <math>OF,</math> the perpendicular bisector of <math>BP.</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
== Video solution == | == Video solution == | ||
| Line 9: | Line 36: | ||
https://youtu.be/bDHtM1wijbY [Shorter solution, video covers all day 1 problems] | https://youtu.be/bDHtM1wijbY [Shorter solution, video covers all day 1 problems] | ||
| + | |||
| + | ==See Also== | ||
| + | |||
| + | {{IMO box|year=2020|before=First Problem|num-a=2}} | ||
| + | |||
| + | [[Category:Olympiad Geometry Problems]] | ||
Latest revision as of 08:29, 28 September 2023
Contents
Problem
Consider the convex quadrilateral ![]() . The point
. The point ![]() is in the interior of
is in the interior of ![]() . The following ratio equalities hold:
. The following ratio equalities hold:
![]() Prove that the following three lines meet in a point: the internal bisectors of angles
Prove that the following three lines meet in a point: the internal bisectors of angles ![]() and
and ![]() and the perpendicular bisector of segment
and the perpendicular bisector of segment ![]() .
.
solution 1
Let the perpendicular bisector of ![]() meet at point
meet at point ![]() , those two lines meet at
, those two lines meet at ![]() at
at ![]() respectively.
respectively.
As the problem states, denote that ![]() . We can express another triple with
. We can express another triple with ![]() as well. Since the perpendicular line of
as well. Since the perpendicular line of ![]() meets
meets ![]() at point
at point ![]() ,
, ![]() , which means that points
, which means that points ![]() are concyclic since
are concyclic since ![]()
Similarly, points ![]() are concyclic as well, which means five points
are concyclic as well, which means five points ![]() are concyclic.,
are concyclic., ![]()
Moreover, since ![]() ,
, ![]() so the angle bisector if the angle
so the angle bisector if the angle ![]() must be the perpendicular line of
must be the perpendicular line of ![]() , so as the angle bisector of
, so as the angle bisector of ![]() , which means those three lines must be concurrent at the circumcenter of the circle containing five points
, which means those three lines must be concurrent at the circumcenter of the circle containing five points ![]() as desired
as desired
~ bluesoul ~ edits by Pearl2008
Solution 2 (Three perpendicular bisectors)
The essence of the proof is the replacement of the bisectors of angles by the perpendicular bisectors of the sides of the cyclic pentagon.
Let ![]() be the circumcenter of
be the circumcenter of ![]() is the perpendicular bisector of
is the perpendicular bisector of ![]() and point
and point ![]() lies on
lies on ![]() Then
Then
![]()
![]() is cyclic.
is cyclic.
![]() the bisector of the
the bisector of the ![]() is the perpendicular bisector of the side
is the perpendicular bisector of the side ![]() of the cyclic
of the cyclic ![]() that passes through the center
that passes through the center ![]()
A similar reasoning can be done for ![]() the perpendicular bisector of
the perpendicular bisector of ![]()
vladimir.shelomovskii@gmail.com, vvsss
Video solution
https://youtu.be/bDHtM1wijbY [Shorter solution, video covers all day 1 problems]
See Also
| 2020 IMO (Problems) • Resources | ||
| Preceded by First Problem |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 2 |
| All IMO Problems and Solutions | ||