Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2020 USAMO Problems/Problem 1"

(→‎Video Solution)
(→‎Video Solution)
Line 1: Line 1:
 
==Problem 1==
 
==Problem 1==
 
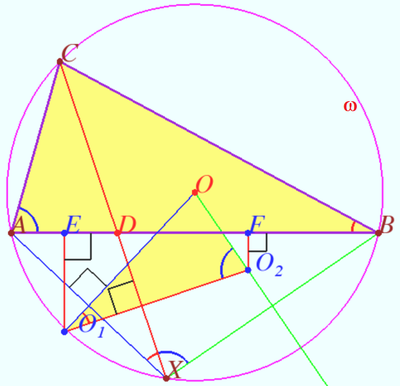
Let <math>ABC</math> be a fixed acute triangle inscribed in a circle <math>\omega</math> with center <math>O</math>. A variable point <math>X</math> is chosen on minor arc <math>AB</math> of <math>\omega</math>, and segments <math>CX</math> and <math>AB</math> meet at <math>D</math>. Denote by <math>O_1</math> and <math>O_2</math> the circumcenters of triangles <math>ADX</math> and <math>BDX</math>, respectively. Determine all points <math>X</math> for which the area of triangle <math>OO_1O_2</math> is minimized.
 
Let <math>ABC</math> be a fixed acute triangle inscribed in a circle <math>\omega</math> with center <math>O</math>. A variable point <math>X</math> is chosen on minor arc <math>AB</math> of <math>\omega</math>, and segments <math>CX</math> and <math>AB</math> meet at <math>D</math>. Denote by <math>O_1</math> and <math>O_2</math> the circumcenters of triangles <math>ADX</math> and <math>BDX</math>, respectively. Determine all points <math>X</math> for which the area of triangle <math>OO_1O_2</math> is minimized.
 +
 +
 +
 +
==Solution==
 +
[[File:2020 USAMO 1.png|400px|right]]
 +
Let <math>E</math> be midpoint <math>AD.</math> Let <math>F</math> be midpoint <math>BD \implies</math>
 +
<cmath>EF = ED + FD = \frac {AD}{2} + \frac {BD}{2} = \frac {AB}{2}.</cmath>
 +
<math>E</math> and <math>F</math> are the bases of perpendiculars dropped from <math>O_1</math> and <math>O_2,</math> respectively.
 +
 +
Therefore  <math>O_1O_2 \ge EF =  \frac {AB}{2}.</math>
 +
 +
<cmath>CX \perp  O_1O_2, AX \perp  O_1O \implies \angle O O_1O_2 = \angle AXC</cmath>
 +
<math>\angle AXC = \angle ABC (AXBC</math> is cyclic) <math>\implies \angle O O_1O_2 = \angle ABC.</math>
 +
 +
Similarly <math>\angle BAC = \angle O O_2 O_1 \implies  \triangle ABC \sim \triangle O_2 O_1O.</math>
 +
 +
The area of <math>\triangle OO_1O_2</math> is minimized if <math>CX \perp AB</math> because
 +
<math></math>\frac {[OO_1O_2]} {[ABC]} = (\frac {O_1 O_2} {AB})^2 \ge (\frac {EF} {AB})^2 = \frac {1}{4}$.
 +
 +
  
  

Revision as of 15:29, 15 September 2022

Problem 1

Let $ABC$ be a fixed acute triangle inscribed in a circle $\omega$ with center $O$. A variable point $X$ is chosen on minor arc $AB$ of $\omega$, and segments $CX$ and $AB$ meet at $D$. Denote by $O_1$ and $O_2$ the circumcenters of triangles $ADX$ and $BDX$, respectively. Determine all points $X$ for which the area of triangle $OO_1O_2$ is minimized.


Solution

2020 USAMO 1.png

Let $E$ be midpoint $AD.$ Let $F$ be midpoint $BD \implies$ \[EF = ED + FD = \frac {AD}{2} + \frac {BD}{2} = \frac {AB}{2}.\] $E$ and $F$ are the bases of perpendiculars dropped from $O_1$ and $O_2,$ respectively.

Therefore $O_1O_2 \ge EF = \frac {AB}{2}.$

\[CX \perp O_1O_2, AX \perp O_1O \implies \angle O O_1O_2 = \angle AXC\] $\angle AXC = \angle ABC (AXBC$ is cyclic) $\implies \angle O O_1O_2 = \angle ABC.$

Similarly $\angle BAC = \angle O O_2 O_1 \implies \triangle ABC \sim \triangle O_2 O_1O.$

The area of $\triangle OO_1O_2$ is minimized if $CX \perp AB$ because $$ (Error compiling LaTeX. Unknown error_msg)\frac {[OO_1O_2]} {[ABC]} = (\frac {O_1 O_2} {AB})^2 \ge (\frac {EF} {AB})^2 = \frac {1}{4}$.



Video Solution

https://www.youtube.com/watch?v=m157cfw0vdE

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2020_USAMO_Problems/Problem_1&oldid=178234"