Difference between revisions of "2021 AIME II Problems/Problem 5"
(→Solution 7) |
MRENTHUSIASM (talk | contribs) m (→Solution 7) |
||
| Line 186: | Line 186: | ||
== Solution 7 == | == Solution 7 == | ||
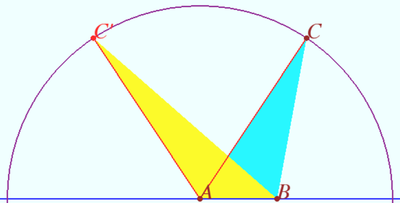
[[File:2021 AIME II 5.png|400px|right]] | [[File:2021 AIME II 5.png|400px|right]] | ||
| − | Let's rephrase the condition. It is required to find such values of the area of an obtuse triangle with sides 4 and 10, when there is exactly one such obtuse triangle. In the diagram, <math>AB = 4, AC = 10.</math> | + | Let's rephrase the condition. It is required to find such values of the area of an obtuse triangle with sides <math>4</math> and <math>10,</math> when there is exactly one such obtuse triangle. In the diagram, <math>AB = 4, AC = 10.</math> |
| − | The largest area of triangle with sides <math>4</math> and <math>10</math> is <math>20</math> for a right triangle with legs <math>4</math> and <math>10 | + | The largest area of triangle with sides <math>4</math> and <math>10</math> is <math>20</math> for a right triangle with legs <math>4</math> and <math>10</math> (<math>AC\perp AB</math>). |
The diagram shows triangles with equal heights. The yellow triangle <math>ABC'</math> has the longest side <math>BC',</math> the blue triangle <math>ABC</math> has the longest side <math>AC.</math> | The diagram shows triangles with equal heights. The yellow triangle <math>ABC'</math> has the longest side <math>BC',</math> the blue triangle <math>ABC</math> has the longest side <math>AC.</math> | ||
Revision as of 16:31, 21 June 2022
Contents
Problem
For positive real numbers ![]() , let
, let ![]() denote the set of all obtuse triangles that have area
denote the set of all obtuse triangles that have area ![]() and two sides with lengths
and two sides with lengths ![]() and
and ![]() . The set of all
. The set of all ![]() for which
for which ![]() is nonempty, but all triangles in
is nonempty, but all triangles in ![]() are congruent, is an interval
are congruent, is an interval ![]() . Find
. Find ![]() .
.
Solution 1
We start by defining a triangle. The two small sides MUST add to a larger sum than the long side. We are given ![]() and
and ![]() as the sides, so we know that the
as the sides, so we know that the ![]() rd side is between
rd side is between ![]() and
and ![]() , exclusive. We also have to consider the word OBTUSE triangles. That means that the two small sides squared is less than the
, exclusive. We also have to consider the word OBTUSE triangles. That means that the two small sides squared is less than the ![]() rd side. So the triangles' sides are between
rd side. So the triangles' sides are between ![]() and
and ![]() exclusive, and the larger bound is between
exclusive, and the larger bound is between ![]() and
and ![]() , exclusive. The area of these triangles are from
, exclusive. The area of these triangles are from ![]() (straight line) to
(straight line) to ![]() on the first "small bound" and the larger bound is between
on the first "small bound" and the larger bound is between ![]() and
and ![]() .
.
![]() is our first equation, and
is our first equation, and ![]() is our
is our ![]() nd equation. Therefore, the area is between
nd equation. Therefore, the area is between ![]() and
and ![]() , so our final answer is
, so our final answer is ![]() .
.
~ARCTICTURN
Solution 2 (Inequalities and Casework)
If ![]() and
and ![]() are the side-lengths of an obtuse triangle with
are the side-lengths of an obtuse triangle with ![]() then both of the following must be satisfied:
then both of the following must be satisfied:
- Triangle Inequality Theorem:

- Pythagorean Inequality Theorem:

For one such obtuse triangle, let ![]() and
and ![]() be its side-lengths and
be its side-lengths and ![]() be its area. We apply casework to its longest side:
be its area. We apply casework to its longest side:
Case (1): The longest side has length ![]() so
so ![]()
By the Triangle Inequality Theorem, we have ![]() from which
from which ![]()
By the Pythagorean Inequality Theorem, we have ![]() from which
from which ![]()
Taking the intersection produces ![]() for this case.
for this case.
At ![]() the obtuse triangle degenerates into a straight line with area
the obtuse triangle degenerates into a straight line with area ![]() at
at ![]() the obtuse triangle degenerates into a right triangle with area
the obtuse triangle degenerates into a right triangle with area ![]() Together, we obtain
Together, we obtain ![]() or
or ![]()
Case (2): The longest side has length ![]() so
so ![]()
By the Triangle Inequality Theorem, we have ![]() from which
from which ![]()
By the Pythagorean Inequality Theorem, we have ![]() from which
from which ![]()
Taking the intersection produces ![]() for this case.
for this case.
At ![]() the obtuse triangle degenerates into a straight line with area
the obtuse triangle degenerates into a straight line with area ![]() at
at ![]() the obtuse triangle degenerates into a right triangle with area
the obtuse triangle degenerates into a right triangle with area ![]() Together, we obtain
Together, we obtain ![]() or
or ![]()
Answer
It is possible for noncongruent obtuse triangles to have the same area. Therefore, all such positive real numbers ![]() are in exactly one of
are in exactly one of ![]() or
or ![]() By the exclusive disjunction, the set of all such
By the exclusive disjunction, the set of all such ![]() is
is ![]() from which
from which ![]()
~MRENTHUSIASM
Solution 3
We have the diagram below.
![[asy] draw((0,0)--(1,2*sqrt(3))); draw((1,2*sqrt(3))--(10,0)); draw((10,0)--(0,0)); label("$A$",(0,0),SW); label("$B$",(1,2*sqrt(3)),N); label("$C$",(10,0),SE); label("$\theta$",(0,0),NE); label("$\alpha$",(1,2*sqrt(3)),SSE); label("$4$",(0,0)--(1,2*sqrt(3)),WNW); label("$10$",(0,0)--(10,0),S); [/asy]](http://latex.artofproblemsolving.com/6/9/4/6940b758ab02beb075b54be2d68de6be1ceb38ec.png)
We proceed by taking cases on the angles that can be obtuse, and finding the ranges for ![]() that they yield .
that they yield .
If angle ![]() is obtuse, then we have that
is obtuse, then we have that ![]() . This is because
. This is because ![]() is attained at
is attained at ![]() , and the area of the triangle is strictly decreasing as
, and the area of the triangle is strictly decreasing as ![]() increases beyond
increases beyond ![]() . This can be observed from
. This can be observed from
![]() by noting that
by noting that ![]() is decreasing in
is decreasing in ![]() .
.
Then, we note that if ![]() is obtuse, we have
is obtuse, we have ![]() . This is because we get
. This is because we get ![]() when
when ![]() , yileding
, yileding ![]() . Then,
. Then, ![]() is decreasing as
is decreasing as ![]() increases by the same argument as before.
increases by the same argument as before.
![]() cannot be obtuse since
cannot be obtuse since ![]() .
.
Now we have the intervals ![]() and
and ![]() for the cases where
for the cases where ![]() and
and ![]() are obtuse, respectively. We are looking for the
are obtuse, respectively. We are looking for the ![]() that are in exactly one of these intervals, and because
that are in exactly one of these intervals, and because ![]() , the desired range is
, the desired range is
![]() giving
giving ![]()
Solution 4
Note: Archimedes15 Solution which I added an answer
here are two cases. Either the ![]() and
and ![]() are around an obtuse angle or the
are around an obtuse angle or the ![]() and
and ![]() are around an acute triangle. If they are around the obtuse angle, the area of that triangle is
are around an acute triangle. If they are around the obtuse angle, the area of that triangle is ![]() as we have
as we have ![]() and
and ![]() is at most
is at most ![]() . Note that for the other case, the side lengths around the obtuse angle must be
. Note that for the other case, the side lengths around the obtuse angle must be ![]() and
and ![]() where we have
where we have ![]() . Using the same logic as the other case, the area is at most
. Using the same logic as the other case, the area is at most ![]() . Square and add
. Square and add ![]() and
and ![]() to get the right answer
to get the right answer ![]()
Solution 5 (Circles)
For ![]() we fix
we fix ![]() and
and ![]() Without the loss of generality, we consider
Without the loss of generality, we consider ![]() on only one side of
on only one side of ![]()
As shown below, all locations for ![]() at which
at which ![]() is an obtuse triangle are indicated in red, excluding the endpoints.
is an obtuse triangle are indicated in red, excluding the endpoints.
![[asy] /* Made by MRENTHUSIASM */ size(300); pair A, B, O, P, Q, C1, C2, D; A = origin; B = (10,0); O = midpoint(A--B); P = B - (4,0); Q = B + (4,0); C1 = intersectionpoints(D--D+(100,0),Arc(B,Q,P))[1]; C2 = B + (0,4); D = intersectionpoint(Arc(O,B,A),Arc(B,Q,P)); draw(Arc(O,B,A)^^Arc(B,C2,D)^^A--Q); draw(Arc(B,Q,C2)^^Arc(B,D,P),red); dot("$A$", A, 1.5*S, linewidth(4.5)); dot("$B$", B, 1.5*S, linewidth(4.5)); dot(O, linewidth(4.5)); dot(P^^C2^^D^^Q, linewidth(0.8), UnFill); Label L1 = Label("$10$", align=(0,0), position=MidPoint, filltype=Fill(3,0,white)); Label L2 = Label("$4$", align=(0,0), position=MidPoint, filltype=Fill(3,0,white)); draw(A-(0,2)--B-(0,2), L=L1, arrow=Arrows(),bar=Bars(15)); draw(B-(0,2)--Q-(0,2), L=L2, arrow=Arrows(),bar=Bars(15)); label("$\angle C$ obtuse",(midpoint(Arc(B,D,P)).x,2),2.5*W,red); label("$\angle B$ obtuse",(midpoint(Arc(B,Q,C2)).x,2),5*E,red); [/asy]](http://latex.artofproblemsolving.com/1/8/e/18e2bd9cca76db19a046b9e4a1594f5a5d3a91d2.png) Note that:
Note that:
- The region in which
 is obtuse is determined by construction.
is obtuse is determined by construction. - The region in which
 is obtuse is determined by the corollaries of the Inscribed Angle Theorem.
is obtuse is determined by the corollaries of the Inscribed Angle Theorem.
For any fixed value of ![]() the height from
the height from ![]() is fixed. We need obtuse
is fixed. We need obtuse ![]() to be unique, so there can only be one possible location for
to be unique, so there can only be one possible location for ![]() As shown below, all possible locations for
As shown below, all possible locations for ![]() are on minor arc
are on minor arc ![]() including
including ![]() but excluding
but excluding ![]()
![[asy] /* Made by MRENTHUSIASM */ size(250); pair A, B, O, P, Q, C1, C2, D; A = origin; B = (10,0); O = midpoint(A--B); P = B - (4,0); Q = B + (4,0); C2 = B + (0,4); D = intersectionpoint(Arc(O,B,A),Arc(B,Q,P)); C1 = intersectionpoint(D--D+(100,0),Arc(B,Q,C2)); draw(Arc(O,B,A)^^Arc(B,C2,D)^^A--Q); draw(Arc(B,Q,C1)^^Arc(B,D,P),red); draw(Arc(B,C1,C2),green); draw((A.x,D.y)--(Q.x,D.y),dashed); dot("$A$", A, 1.5*S, linewidth(4.5)); dot("$B$", B, 1.5*S, linewidth(4.5)); dot("$D$", D, 1.5*dir(75), linewidth(0.8), UnFill); dot("$C_2$", C2, 1.5*N, linewidth(4.5)); dot("$C_1$", C1, 1.5*dir(C1-B), linewidth(4.5)); dot(O, linewidth(4.5)); dot(P^^C2^^Q, linewidth(0.8), UnFill); dot(C1, green+linewidth(4.5)); Label L1 = Label("$10$", align=(0,0), position=MidPoint, filltype=Fill(3,0,white)); Label L2 = Label("$4$", align=(0,0), position=MidPoint, filltype=Fill(3,0,white)); draw(A-(0,2)--B-(0,2), L=L1, arrow=Arrows(),bar=Bars(15)); draw(B-(0,2)--Q-(0,2), L=L2, arrow=Arrows(),bar=Bars(15)); [/asy]](http://latex.artofproblemsolving.com/d/5/8/d5866dc17da756aa17b80a18837c21dd1555de0c.png) Let the brackets denote areas:
Let the brackets denote areas:
- If
 then
then ![$[ABC]$](//latex.artofproblemsolving.com/d/3/3/d33cc80fa8f093e155c5be46d2e5d9da3d7e1ef5.png) will be minimized (attainable). By the same base and height and the Inscribed Angle Theorem, we have
will be minimized (attainable). By the same base and height and the Inscribed Angle Theorem, we have
![\begin{align*} [ABC]&=[ABD] \\ &=\frac12\cdot BD\cdot DA \\ &=\frac12\cdot BD\cdot \sqrt{AB^2-BD^2} \\ &=\frac12\cdot 4\cdot \sqrt{10^2-4^2} \\ &=2\sqrt{84}. \end{align*}](//latex.artofproblemsolving.com/9/2/7/927b1f1b76a8b725a60b4b3904816b98df28d33d.png)
- If
 then
then ![$[ABC]$](//latex.artofproblemsolving.com/d/3/3/d33cc80fa8f093e155c5be46d2e5d9da3d7e1ef5.png) will be maximized (unattainable). For this right triangle, we have
will be maximized (unattainable). For this right triangle, we have
![\begin{align*} [ABC]&=\frac12\cdot AB\cdot BC \\ &=\frac12\cdot 10\cdot 4 \\ &=20. \end{align*}](//latex.artofproblemsolving.com/e/0/f/e0f25498d2303979005c472c701f20525459cdaa.png)
Finally, the set of all such ![]() is
is ![]() from which
from which ![]()
~MRENTHUSIASM (credit given to Snowfan)
Solution 6
Let a triangle in ![]() be
be ![]() , where
, where ![]() and
and ![]() . We will proceed with two cases:
. We will proceed with two cases:
Case 1: ![]() is obtuse. If
is obtuse. If ![]() is obtuse, then, if we imagine
is obtuse, then, if we imagine ![]() as the base of our triangle, the height can be anything in the range
as the base of our triangle, the height can be anything in the range ![]() ; therefore, the area of the triangle will fall in the range of
; therefore, the area of the triangle will fall in the range of ![]() .
.
Case 2: ![]() is obtuse. Then, if we imagine
is obtuse. Then, if we imagine ![]() as the base of our triangle, the height can be anything in the range
as the base of our triangle, the height can be anything in the range ![]() . Therefore, the area of the triangle will fall in the range of
. Therefore, the area of the triangle will fall in the range of ![]() .
.
If ![]() , there will exist two types of triangles in
, there will exist two types of triangles in ![]() - one type with
- one type with ![]() obtuse; the other type with
obtuse; the other type with ![]() obtuse. If
obtuse. If ![]() , as we just found,
, as we just found, ![]() cannot be obtuse, so therefore, there is only one type of triangle - the one in which
cannot be obtuse, so therefore, there is only one type of triangle - the one in which ![]() is obtuse. Also, if
is obtuse. Also, if ![]() , no triangle exists with lengths
, no triangle exists with lengths ![]() and
and ![]() . Therefore,
. Therefore, ![]() is in the range
is in the range ![]() , so our answer is
, so our answer is ![]() .
.
Alternatively, refer to Solution 5 for the geometric interpretation.
~ihatemath123
Solution 7
Let's rephrase the condition. It is required to find such values of the area of an obtuse triangle with sides ![]() and
and ![]() when there is exactly one such obtuse triangle. In the diagram,
when there is exactly one such obtuse triangle. In the diagram, ![]()
The largest area of triangle with sides ![]() and
and ![]() is
is ![]() for a right triangle with legs
for a right triangle with legs ![]() and
and ![]() (
(![]() ).
).
The diagram shows triangles with equal heights. The yellow triangle ![]() has the longest side
has the longest side ![]() the blue triangle
the blue triangle ![]() has the longest side
has the longest side ![]() If
If ![]() then
then![]() the area is equal to
the area is equal to ![]() In the interval, the blue triangle
In the interval, the blue triangle ![]() is acute-angled, the yellow triangle
is acute-angled, the yellow triangle ![]() is obtuse-angled. Their heights and areas are equal. The condition is met.
is obtuse-angled. Their heights and areas are equal. The condition is met.
If the area is less than ![]() both triangles are obtuse, not equal, so the condition is not met.
both triangles are obtuse, not equal, so the condition is not met.
Shelomovskii, vvsss, www.deoma-cmd.ru
See Also
| 2021 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 4 |
Followed by Problem 6 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 





![\begin{align*} [ABC]&=[ABD] \\ &=\frac12\cdot BD\cdot DA \\ &=\frac12\cdot BD\cdot \sqrt{AB^2-BD^2} \\ &=\frac12\cdot 4\cdot \sqrt{10^2-4^2} \\ &=2\sqrt{84}. \end{align*}](http://latex.artofproblemsolving.com/9/2/7/927b1f1b76a8b725a60b4b3904816b98df28d33d.png)
![\begin{align*} [ABC]&=\frac12\cdot AB\cdot BC \\ &=\frac12\cdot 10\cdot 4 \\ &=20. \end{align*}](http://latex.artofproblemsolving.com/e/0/f/e0f25498d2303979005c472c701f20525459cdaa.png)