Difference between revisions of "2021 AIME I Problems/Problem 11"
m |
Y.grace.yu (talk | contribs) (→Added Alternative Solution) |
||
| Line 10: | Line 10: | ||
From Ptolemy's theorem, we have that <math>(BD)(AC) = 4\times6+5\times7 = 59</math>. From Brahmagupta's Formula, <math>[ABCD] = \sqrt{(11-4)(11-5)(11-6)(11-7)} = 2\sqrt{210}</math>. But the area is also <math>\frac{1}{2}(BD)(AC)\sin\theta = \frac{59}{2}\sin\theta</math>, so <math>\sin \theta = \frac{4\sqrt{210}}{59} \implies \cos \theta = \frac{11}{59}</math>. Then the desired fraction is <math>(4+5+6+7)\cos\theta = \frac{242}{59}</math> for an answer of <math>\boxed{301}</math>. | From Ptolemy's theorem, we have that <math>(BD)(AC) = 4\times6+5\times7 = 59</math>. From Brahmagupta's Formula, <math>[ABCD] = \sqrt{(11-4)(11-5)(11-6)(11-7)} = 2\sqrt{210}</math>. But the area is also <math>\frac{1}{2}(BD)(AC)\sin\theta = \frac{59}{2}\sin\theta</math>, so <math>\sin \theta = \frac{4\sqrt{210}}{59} \implies \cos \theta = \frac{11}{59}</math>. Then the desired fraction is <math>(4+5+6+7)\cos\theta = \frac{242}{59}</math> for an answer of <math>\boxed{301}</math>. | ||
| + | |||
| + | ==Finding <math>\cos{x}</math> 2== | ||
| + | The angle <math>\theta</math> between diagonals satisfies <cmath>\tan{\frac{\theta}{2}}=\sqrt{\frac{(s-b)(s-d}{(s-a)(s-c)}}</cmath> (see https://en.wikipedia.org/wiki/Cyclic_quadrilateral#Angle_formulas). | ||
| + | Thus, <cmath>\tan{\frac{\theta}{2}}=\sqrt{\frac{(11-4)(11-6)}{(11-5)(11-7)}}</cmath> or <cmath>\tan{\frac{\theta}{2}}=\sqrt{\frac{(11-5)(11-7)}{(11-4)(11-6)}}</cmath> | ||
| + | That is, <math>\tan^2{\frac{\theta}{2}}=\frac{1-\cos^2{\frac{\theta}{2}}}{\cos^2{\frac{\theta}{2}}}=\frac{24}{35}</math> or <math>\frac{35}{24}</math> | ||
| + | Thus, <math>\cos^2{\frac{\theta}{2}}=\frac{35}{59}</math> or <math>\frac{24}{59}</math> | ||
| + | <cmath>\cos{\theta}=2\cos^2{\frac{\theta}{2}}-1=\frac{\pm11}{59}</cmath> | ||
| + | In this context, <math>\cos{\theta}>0</math>. Thus, <math>\cos{\theta}=\frac{11}{59}</math> | ||
| + | <cmath>Ans=22*\cos{\theta}=22*\frac{11}{59}=\frac{242}{59}=\frac{m}{n}</cmath> | ||
| + | <cmath>m+n=242+59=\boxed{301}</cmath> | ||
| + | ~y.grace.yu | ||
| + | |||
==See also== | ==See also== | ||
{{AIME box|year=2021|n=I|num-b=10|num-a=12}} | {{AIME box|year=2021|n=I|num-b=10|num-a=12}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 02:30, 12 March 2021
Contents
Problem
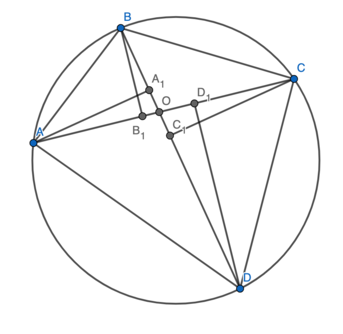
Let ![]() be a cyclic quadrilateral with
be a cyclic quadrilateral with ![]() and
and ![]() . Let
. Let ![]() and
and ![]() be the feet of the perpendiculars from
be the feet of the perpendiculars from ![]() and
and ![]() , respectively, to line
, respectively, to line ![]() and let
and let ![]() and
and ![]() be the feet of the perpendiculars from
be the feet of the perpendiculars from ![]() and
and ![]() respectively, to line
respectively, to line ![]() . The perimeter of
. The perimeter of ![]() is
is ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution
Let ![]() be the intersection of
be the intersection of ![]() and
and ![]() . Let
. Let ![]() .
.
Firstly, since ![]() , we deduce that
, we deduce that ![]() is cyclic. This implies that
is cyclic. This implies that ![]() , with a ratio of
, with a ratio of ![]() . This means that
. This means that ![]() . Similarly,
. Similarly, ![]() . Hence
. Hence ![]() It therefore only remains to find
It therefore only remains to find ![]() .
.
From Ptolemy's theorem, we have that ![]() . From Brahmagupta's Formula,
. From Brahmagupta's Formula, ![]() . But the area is also
. But the area is also ![]() , so
, so ![]() . Then the desired fraction is
. Then the desired fraction is ![]() for an answer of
for an answer of ![]() .
.
Finding  2
2
The angle ![]() between diagonals satisfies
between diagonals satisfies ![\[\tan{\frac{\theta}{2}}=\sqrt{\frac{(s-b)(s-d}{(s-a)(s-c)}}\]](http://latex.artofproblemsolving.com/a/1/6/a1687bce2bc34d2a73aa7498c7a9ca993bb9d166.png) (see https://en.wikipedia.org/wiki/Cyclic_quadrilateral#Angle_formulas).
Thus,
(see https://en.wikipedia.org/wiki/Cyclic_quadrilateral#Angle_formulas).
Thus, ![\[\tan{\frac{\theta}{2}}=\sqrt{\frac{(11-4)(11-6)}{(11-5)(11-7)}}\]](http://latex.artofproblemsolving.com/8/9/9/899281a447db8934bc4dce2667cc8ad64656fb4d.png) or
or ![\[\tan{\frac{\theta}{2}}=\sqrt{\frac{(11-5)(11-7)}{(11-4)(11-6)}}\]](http://latex.artofproblemsolving.com/f/8/b/f8b3a3a8c72ce4ff55ed062a76e4ebc8147f633b.png) That is,
That is, ![]() or
or ![]() Thus,
Thus, ![]() or
or ![]()
![]() In this context,
In this context, ![]() . Thus,
. Thus, ![]()
![]()
![]() ~y.grace.yu
~y.grace.yu
See also
| 2021 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 10 |
Followed by Problem 12 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.