Difference between revisions of "2021 AIME I Problems/Problem 11"
m |
m (→Solution 2 (Finding cos{x})) |
||
| (6 intermediate revisions by 3 users not shown) | |||
| Line 2: | Line 2: | ||
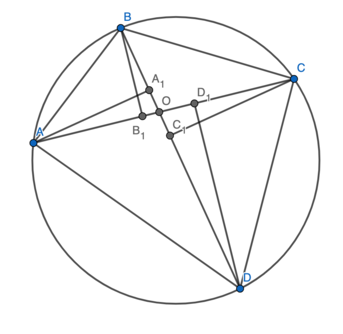
Let <math>ABCD</math> be a cyclic quadrilateral with <math>AB=4,BC=5,CD=6,</math> and <math>DA=7</math>. Let <math>A_1</math> and <math>C_1</math> be the feet of the perpendiculars from <math>A</math> and <math>C</math>, respectively, to line <math>BD,</math> and let <math>B_1</math> and <math>D_1</math> be the feet of the perpendiculars from <math>B</math> and <math>D,</math> respectively, to line <math>AC</math>. The perimeter of <math>A_1B_1C_1D_1</math> is <math>\frac mn</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>. | Let <math>ABCD</math> be a cyclic quadrilateral with <math>AB=4,BC=5,CD=6,</math> and <math>DA=7</math>. Let <math>A_1</math> and <math>C_1</math> be the feet of the perpendiculars from <math>A</math> and <math>C</math>, respectively, to line <math>BD,</math> and let <math>B_1</math> and <math>D_1</math> be the feet of the perpendiculars from <math>B</math> and <math>D,</math> respectively, to line <math>AC</math>. The perimeter of <math>A_1B_1C_1D_1</math> is <math>\frac mn</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>. | ||
| − | == | + | ==Diagram== |
| − | [[File:Leonard_my_dude's_image.png]] | + | [[File:Leonard_my_dude's_image.png|center]] |
| + | ==Solution 1== | ||
Let <math>O</math> be the intersection of <math>AC</math> and <math>BD</math>. Let <math>\theta = \angle AOB</math>. | Let <math>O</math> be the intersection of <math>AC</math> and <math>BD</math>. Let <math>\theta = \angle AOB</math>. | ||
| Line 10: | Line 11: | ||
From Ptolemy's theorem, we have that <math>(BD)(AC) = 4\times6+5\times7 = 59</math>. From Brahmagupta's Formula, <math>[ABCD] = \sqrt{(11-4)(11-5)(11-6)(11-7)} = 2\sqrt{210}</math>. But the area is also <math>\frac{1}{2}(BD)(AC)\sin\theta = \frac{59}{2}\sin\theta</math>, so <math>\sin \theta = \frac{4\sqrt{210}}{59} \implies \cos \theta = \frac{11}{59}</math>. Then the desired fraction is <math>(4+5+6+7)\cos\theta = \frac{242}{59}</math> for an answer of <math>\boxed{301}</math>. | From Ptolemy's theorem, we have that <math>(BD)(AC) = 4\times6+5\times7 = 59</math>. From Brahmagupta's Formula, <math>[ABCD] = \sqrt{(11-4)(11-5)(11-6)(11-7)} = 2\sqrt{210}</math>. But the area is also <math>\frac{1}{2}(BD)(AC)\sin\theta = \frac{59}{2}\sin\theta</math>, so <math>\sin \theta = \frac{4\sqrt{210}}{59} \implies \cos \theta = \frac{11}{59}</math>. Then the desired fraction is <math>(4+5+6+7)\cos\theta = \frac{242}{59}</math> for an answer of <math>\boxed{301}</math>. | ||
| + | |||
| + | ==Solution 2 (Finding cos{x})== | ||
| + | The angle <math>\theta</math> between diagonals satisfies <cmath>\tan{\frac{\theta}{2}}=\sqrt{\frac{(s-b)(s-d)}{(s-a)(s-c)}}</cmath> (see https://en.wikipedia.org/wiki/Cyclic_quadrilateral#Angle_formulas). | ||
| + | Thus, <cmath>\tan{\frac{\theta}{2}}=\sqrt{\frac{(11-4)(11-6)}{(11-5)(11-7)}}</cmath> or <cmath>\tan{\frac{\theta}{2}}=\sqrt{\frac{(11-5)(11-7)}{(11-4)(11-6)}}</cmath> | ||
| + | That is, <math>\tan^2{\frac{\theta}{2}}=\frac{1-\cos^2{\frac{\theta}{2}}}{\cos^2{\frac{\theta}{2}}}=\frac{24}{35}</math> or <math>\frac{35}{24}</math> | ||
| + | Thus, <math>\cos^2{\frac{\theta}{2}}=\frac{35}{59}</math> or <math>\frac{24}{59}</math> | ||
| + | <cmath>\cos{\theta}=2\cos^2{\frac{\theta}{2}}-1=\frac{\pm11}{59}</cmath> | ||
| + | In this context, <math>\cos{\theta}>0</math>. Thus, <math>\cos{\theta}=\frac{11}{59}</math> | ||
| + | <cmath>Ans=22*\cos{\theta}=22*\frac{11}{59}=\frac{242}{59}=\frac{m}{n}</cmath> | ||
| + | <cmath>m+n=242+59=\boxed{301}</cmath> | ||
| + | ~y.grace.yu | ||
| + | |||
| + | ==Solution 3 (Pythagorean Theorem)== | ||
| + | We assume that the two quadrilateral mentioned in the problem are similar (due to both of them being cyclic). Note that by Ptolemy’s, one of the diagonals has length <math>\sqrt{4 \cdot 6 + 5 \cdot 7} = \sqrt{59}.</math> WLOG we focus on diagonal <math>BD.</math> To find the diagonal of the inner quadrilateral, we drop the altitude from <math>A</math> and <math>C</math> and calculate the length of <math>A_1C_1.</math> Let <math>x</math> be <math>A_1D</math> (Thus <math>A_1B = \sqrt{59} - x.</math> By Pythagorean theorem, we have <cmath>49 - x^2 = 16 - (\sqrt{59} - x)^2 \implies 92 = 2\sqrt{59}x \implies x = \frac{46}{\sqrt{59}} = \frac{46\sqrt{59}}{59}.</cmath> Now let <math>y</math> be <math>C_1D.</math> (thus making <math>C_1B = \sqrt{59} - y</math>). Similarly, we have <cmath>36 - y^2 = 25 - (\sqrt{59} - y)^2 \implies 70 = 2\sqrt{59}y \implies y = \frac{35}{\sqrt{59}} = \frac{35\sqrt{59}}{59}.</cmath> We see that <math>A_1C_1</math>, the scaled down diagonal is just <math>x - y = \frac{11\sqrt{59}}{59},</math> which is <math>\frac{\frac{11\sqrt{59}}{59}}{\sqrt{59}} = \frac{11}{59}</math> times our original diagonal <math>BD,</math> implying a scale factor of <math>\frac{11}{59}.</math> Thus, due to perimeters scaling linearly, the perimeter of the new quadrilateral is simply <math>\frac{11}{59} \cdot 22 = \frac{242}{59},</math> making our answer <math>242+59 = \boxed{301}.</math> | ||
| + | -fidgetboss_4000 | ||
| + | |||
==See also== | ==See also== | ||
{{AIME box|year=2021|n=I|num-b=10|num-a=12}} | {{AIME box|year=2021|n=I|num-b=10|num-a=12}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 00:29, 23 April 2021
Contents
Problem
Let ![]() be a cyclic quadrilateral with
be a cyclic quadrilateral with ![]() and
and ![]() . Let
. Let ![]() and
and ![]() be the feet of the perpendiculars from
be the feet of the perpendiculars from ![]() and
and ![]() , respectively, to line
, respectively, to line ![]() and let
and let ![]() and
and ![]() be the feet of the perpendiculars from
be the feet of the perpendiculars from ![]() and
and ![]() respectively, to line
respectively, to line ![]() . The perimeter of
. The perimeter of ![]() is
is ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Diagram
Solution 1
Let ![]() be the intersection of
be the intersection of ![]() and
and ![]() . Let
. Let ![]() .
.
Firstly, since ![]() , we deduce that
, we deduce that ![]() is cyclic. This implies that
is cyclic. This implies that ![]() , with a ratio of
, with a ratio of ![]() . This means that
. This means that ![]() . Similarly,
. Similarly, ![]() . Hence
. Hence ![]() It therefore only remains to find
It therefore only remains to find ![]() .
.
From Ptolemy's theorem, we have that ![]() . From Brahmagupta's Formula,
. From Brahmagupta's Formula, ![]() . But the area is also
. But the area is also ![]() , so
, so ![]() . Then the desired fraction is
. Then the desired fraction is ![]() for an answer of
for an answer of ![]() .
.
Solution 2 (Finding cos{x})
The angle ![]() between diagonals satisfies
between diagonals satisfies ![\[\tan{\frac{\theta}{2}}=\sqrt{\frac{(s-b)(s-d)}{(s-a)(s-c)}}\]](http://latex.artofproblemsolving.com/9/7/c/97c3d3b8825eea07df794427667b774cbf27b7c8.png) (see https://en.wikipedia.org/wiki/Cyclic_quadrilateral#Angle_formulas).
Thus,
(see https://en.wikipedia.org/wiki/Cyclic_quadrilateral#Angle_formulas).
Thus, ![\[\tan{\frac{\theta}{2}}=\sqrt{\frac{(11-4)(11-6)}{(11-5)(11-7)}}\]](http://latex.artofproblemsolving.com/8/9/9/899281a447db8934bc4dce2667cc8ad64656fb4d.png) or
or ![\[\tan{\frac{\theta}{2}}=\sqrt{\frac{(11-5)(11-7)}{(11-4)(11-6)}}\]](http://latex.artofproblemsolving.com/f/8/b/f8b3a3a8c72ce4ff55ed062a76e4ebc8147f633b.png) That is,
That is, ![]() or
or ![]() Thus,
Thus, ![]() or
or ![]()
![]() In this context,
In this context, ![]() . Thus,
. Thus, ![]()
![]()
![]() ~y.grace.yu
~y.grace.yu
Solution 3 (Pythagorean Theorem)
We assume that the two quadrilateral mentioned in the problem are similar (due to both of them being cyclic). Note that by Ptolemy’s, one of the diagonals has length ![]() WLOG we focus on diagonal
WLOG we focus on diagonal ![]() To find the diagonal of the inner quadrilateral, we drop the altitude from
To find the diagonal of the inner quadrilateral, we drop the altitude from ![]() and
and ![]() and calculate the length of
and calculate the length of ![]() Let
Let ![]() be
be ![]() (Thus
(Thus ![]() By Pythagorean theorem, we have
By Pythagorean theorem, we have ![]() Now let
Now let ![]() be
be ![]() (thus making
(thus making ![]() ). Similarly, we have
). Similarly, we have ![]() We see that
We see that ![]() , the scaled down diagonal is just
, the scaled down diagonal is just ![]() which is
which is ![]() times our original diagonal
times our original diagonal ![]() implying a scale factor of
implying a scale factor of ![]() Thus, due to perimeters scaling linearly, the perimeter of the new quadrilateral is simply
Thus, due to perimeters scaling linearly, the perimeter of the new quadrilateral is simply ![]() making our answer
making our answer ![]() -fidgetboss_4000
-fidgetboss_4000
See also
| 2021 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 10 |
Followed by Problem 12 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.