Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 AIME I Problems/Problem 11"
Line 9: Line 9:
 
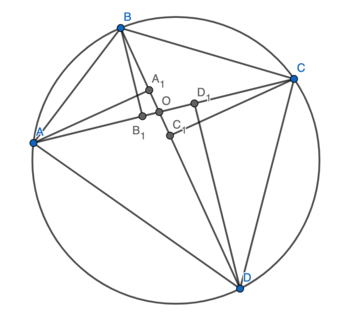
Firstly, since <math>\angle AA_1D = \angle AD_1D = 90^\circ</math>, we deduce that <math>AA_1D_1D</math> is cyclic. This implies that <math>\triangle A_1OD_1 \sim \triangle AOD</math>, with a ratio of <math>\frac{A_1O}{AO} = \cos \angle A_1OA = \cos \theta</math>. This means that <math>\frac{A_1D_1}{AD} = \cos \theta</math>. Similarly, <math>\frac{A_1B_1}{AB} = \frac{B_1C_1}{BC} = \frac{C_1D_1}{CD} = \cos \theta</math>. Hence <cmath>A_1B_1 + B_1C_1 + C_1D_1 + D_1A_1 = (AB + BC + CD + DA)\cos \theta</cmath> It therefore only remains to find <math>\cos \theta</math>.
 
Firstly, since <math>\angle AA_1D = \angle AD_1D = 90^\circ</math>, we deduce that <math>AA_1D_1D</math> is cyclic. This implies that <math>\triangle A_1OD_1 \sim \triangle AOD</math>, with a ratio of <math>\frac{A_1O}{AO} = \cos \angle A_1OA = \cos \theta</math>. This means that <math>\frac{A_1D_1}{AD} = \cos \theta</math>. Similarly, <math>\frac{A_1B_1}{AB} = \frac{B_1C_1}{BC} = \frac{C_1D_1}{CD} = \cos \theta</math>. Hence <cmath>A_1B_1 + B_1C_1 + C_1D_1 + D_1A_1 = (AB + BC + CD + DA)\cos \theta</cmath> It therefore only remains to find <math>\cos \theta</math>.
  
−
From Ptolemy's theorem, we have that <math>(BC)(AC) = 4\times6+5\times7 = 59</math>. From Brahmagupta's Formula, <math>[ABCD] = \sqrt{(11-4)(11-5)(11-6)(11-7)} = 2\sqrt{210}</math>. But the area is also <math>\frac{1}{2}(BC)(AC)\sin\theta = \frac{59}{2}\sin\theta</math>, so <math>\sin \theta = \frac{4\sqrt{210}}{59} \implies \cos \theta = \frac{11}{59}</math>. Then the desired fraction is <math>(4+5+6+7)\cos\theta = \frac{242}{59}</math> for an answer of <math>\boxed{301}</math>.
+
From Ptolemy's theorem, we have that <math>(BC)(AC) = 4\times6+5\times7 = 59</math>. From Brahmagupta's Formula, <math>[ABCD] = \sqrt{(11-4)(11-5)(11-6)(11-7)} = 2\sqrt{210}</math>. But the area is also <math>\frac{1}{2}(BD)(AC)\sin\theta = \frac{59}{2}\sin\theta</math>, so <math>\sin \theta = \frac{4\sqrt{210}}{59} \implies \cos \theta = \frac{11}{59}</math>. Then the desired fraction is <math>(4+5+6+7)\cos\theta = \frac{242}{59}</math> for an answer of <math>\boxed{301}</math>.
 
==See also==
 
==See also==
 
{{AIME box|year=2021|n=I|num-b=10|num-a=12}}
 
{{AIME box|year=2021|n=I|num-b=10|num-a=12}}
 
{{MAA Notice}}
 
{{MAA Notice}}

Revision as of 23:06, 11 March 2021

Problem

Let $ABCD$ be a cyclic quadrilateral with $AB=4,BC=5,CD=6,$ and $DA=7$. Let $A_1$ and $C_1$ be the feet of the perpendiculars from $A$ and $C$, respectively, to line $BD,$ and let $B_1$ and $D_1$ be the feet of the perpendiculars from $B$ and $D,$ respectively, to line $AC$. The perimeter of $A_1B_1C_1D_1$ is $\frac mn$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.

Solution

Leonard my dude's image.png

Let $O$ be the intersection of $AC$ and $BD$. Let $\theta = \angle AOB$.

Firstly, since $\angle AA_1D = \angle AD_1D = 90^\circ$, we deduce that $AA_1D_1D$ is cyclic. This implies that $\triangle A_1OD_1 \sim \triangle AOD$, with a ratio of $\frac{A_1O}{AO} = \cos \angle A_1OA = \cos \theta$. This means that $\frac{A_1D_1}{AD} = \cos \theta$. Similarly, $\frac{A_1B_1}{AB} = \frac{B_1C_1}{BC} = \frac{C_1D_1}{CD} = \cos \theta$. Hence \[A_1B_1 + B_1C_1 + C_1D_1 + D_1A_1 = (AB + BC + CD + DA)\cos \theta\] It therefore only remains to find $\cos \theta$.

From Ptolemy's theorem, we have that $(BC)(AC) = 4\times6+5\times7 = 59$. From Brahmagupta's Formula, $[ABCD] = \sqrt{(11-4)(11-5)(11-6)(11-7)} = 2\sqrt{210}$. But the area is also $\frac{1}{2}(BD)(AC)\sin\theta = \frac{59}{2}\sin\theta$, so $\sin \theta = \frac{4\sqrt{210}}{59} \implies \cos \theta = \frac{11}{59}$. Then the desired fraction is $(4+5+6+7)\cos\theta = \frac{242}{59}$ for an answer of $\boxed{301}$.

See also

2021 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 10 		Followed by
Problem 12
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_AIME_I_Problems/Problem_11&oldid=149148"