Difference between revisions of "2021 AIME I Problems/Problem 15"
m (→Solution 1: Tweaked the LaTeX a little.) |
m (→Diagram) |
||
| (30 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
==Problem== | ==Problem== | ||
Let <math>S</math> be the set of positive integers <math>k</math> such that the two parabolas<cmath>y=x^2-k~~\text{and}~~x=2(y-20)^2-k</cmath>intersect in four distinct points, and these four points lie on a circle with radius at most <math>21</math>. Find the sum of the least element of <math>S</math> and the greatest element of <math>S</math>. | Let <math>S</math> be the set of positive integers <math>k</math> such that the two parabolas<cmath>y=x^2-k~~\text{and}~~x=2(y-20)^2-k</cmath>intersect in four distinct points, and these four points lie on a circle with radius at most <math>21</math>. Find the sum of the least element of <math>S</math> and the greatest element of <math>S</math>. | ||
| − | ==Solution 1== | + | ==Diagram== |
| + | Graph in Desmos: https://www.desmos.com/calculator/37hsgxbygj | ||
| + | |||
| + | ~MRENTHUSIASM | ||
| + | |||
| + | == Solution 1 (Inequalities and Circles) == | ||
| + | Note that <math>y=x^2-k</math> is an upward-opening parabola with the vertex at <math>(0,-k),</math> and <math>x=2(y-20)^2-k</math> is a rightward-opening parabola with the vertex at <math>(-k,20).</math> We consider each condition separately: | ||
| + | <ol style="margin-left: 1.5em;"> | ||
| + | <li>The two parabolas intersect at four distinct points.<p></li> | ||
| + | By a quick sketch, we have two subconditions: | ||
| + | <ol style="margin-left: 1.5em;" type="A"> | ||
| + | <li>The point <math>(-k,20)</math> is on or below the parabola <math>y=x^2-k.</math><p> | ||
| + | We need <math>20\leq(-k)^2-k,</math> from which <math>k\geq5.</math> <p> | ||
| + | Moreover, the point <math>(-k,20)</math> is on the parabola <math>y=x^2-k</math> when <math>k=5.</math> We will prove that the two parabolas intersect at four distinct points at this value of <math>k:</math><p> | ||
| + | Substituting <math>y=x^2-5</math> into <math>x=2(y-20)^2-5,</math> we get <math>x=2\left(\left(x^2-5\right)-20\right)^2-5.</math> Expanding and rearranging give <cmath>2x^4-100x^2-x+1245=0. \hspace{20mm}(\bigstar)</cmath> | ||
| + | By either the graphs of the parabolas or the Rational Root Theorem, we conclude that <math>x=-5</math> is a root of <math>(\bigstar).</math> So, we factor its left side: <cmath>(x+5)\left(2x^3-10x^2-50x+249\right)=0.</cmath> | ||
| + | By either the graphs of the parabolas or Descartes' Rule of Signs, we conclude that <math>2x^3-10x^2-50x+249=0</math> has two positive roots and one negative root such that <math>x\neq-5.</math> So, <math>(\bigstar)</math> has four distinct real roots, or the two parabolas intersect at four distinct points.<p> | ||
| + | For Subcondition A, we deduce that <math>k\geq5.</math> <p> | ||
| + | <u>Remark for Subcondition A</u><p> | ||
| + | Recall that if <math>1\leq k\leq 4,</math> then the point <math>(-k,20)</math> is above the parabola <math>y=x^2-k.</math> It follows that for <math>-k\leq x\leq0:</math> | ||
| + | <ul style="list-style-type:square;"> | ||
| + | <li>The maximum value of <math>y</math> for the parabola <math>y=x^2-k</math> occurs at <math>x=-k,</math> from which <math>y=k^2-k\leq12.</math></li><p> | ||
| + | <li>The minimum value of <math>y</math> for the parabola <math>x=2(y-20)^2-k</math> occurs at <math>x=0,</math> from which <math>y=20-\sqrt{\frac k2}>18.</math></li><p> | ||
| + | </ul> | ||
| + | Clearly, the parabola <math>x=2(y-20)^2-k</math> and the left half of the parabola <math>y=x^2-k</math> do not intersect. Therefore, the two parabolas do not intersect at four distinct points. | ||
| + | </li> | ||
| + | <li>The point <math>(0,-k)</math> is on or below the parabola <math>x=2(y-20)^2-k.</math><p> | ||
| + | The lower half of the parabola <math>x=2(y-20)^2-k</math> is <math>y=20-\sqrt{\frac{x+k}{2}}.</math> We need <math>-k\leq20-\sqrt{\frac k2},</math> which holds for all values of <math>k.</math><p> | ||
| + | For Subcondition B, we deduce that <math>k</math> can be any positive integer. | ||
| + | </li> | ||
| + | </ol> | ||
| + | <b>For Condition 1, we obtain <math>\boldsymbol{k\geq5}</math> by taking the intersection of Subconditions A and B.</b> | ||
| + | <li>The four points of intersection lie on a circle with radius at most <math>21.</math><p> | ||
| + | For equations of circles, the coefficients of <math>x^2</math> and <math>y^2</math> must be the same. So, we add the equation <math>y=x^2-k</math> to half the equation <math>x=2(y-20)^2-k:</math> <cmath>y+\frac12x=x^2+(y-20)^2-\frac32k.</cmath> | ||
| + | We expand, rearrange, and complete the squares: | ||
| + | <cmath>\begin{align*} | ||
| + | y+\frac12x&=x^2+y^2-40y+400-\frac32k \\ | ||
| + | \frac32k-400&=\left(x^2-\frac12x\right)+\left(y^2-41y\right) \\ | ||
| + | \frac32k-400+\frac{1}{16}+\frac{1681}{4}&=\left(x-\frac14\right)^2+\left(y-\frac{41}{2}\right)^2. | ||
| + | \end{align*}</cmath> | ||
| + | We need <math>\frac32k-400+\frac{1}{16}+\frac{1681}{4}\leq21^2,</math> from which <math>k\leq\left\lfloor\frac{6731}{24}\right\rfloor=280.</math><p> | ||
| + | <b>For Condition 2, we obtain <math>\boldsymbol{k\leq280.}</math></b> | ||
| + | </li> | ||
| + | </ol> | ||
| + | Taking the intersection of Conditions 1 and 2 produces <math>5\leq k\leq280.</math> Therefore, the answer is <math>5+280=\boxed{285}.</math> | ||
| + | |||
| + | ~MRENTHUSIASM | ||
| + | |||
| + | == Solution 2 (Translations, Inequalities, Circles) == | ||
| + | |||
| + | Make the translation <math>y \rightarrow y+20</math> to obtain <math>20+y=x^2-k</math> and <math>x=2y^2-k</math>. Multiply the first equation by <math>2</math> and sum, we see that <math>2(x^2+y^2)=3k+40+2y+x</math>. Completing the square gives us <math>\left(y- \frac{1}{2}\right)^2+\left(x - \frac{1}{4}\right)^2 = \frac{325+24k}{16}</math>; this explains why the two parabolas intersect at four points that lie on a circle*. For the upper bound, observe that <math>LHS \leq 21^2=441 \rightarrow 24k \leq 6731</math>, so <math>k \leq 280</math>. | ||
| + | |||
| + | For the lower bound, we need to ensure there are <math>4</math> intersections to begin with. (Here I'm using the un-translated coordinates.) Draw up a graph, and realize that two intersections are guaranteed, on the so called "right branch" of <math>y=x^2-k</math>. As we increase the value of <math>k</math>, two more intersections appear on the "left branch": | ||
| + | |||
| + | <math>k=4</math> does not work because the "leftmost" point of <math>x=2(y-20)^2-4</math> is <math>(-4,20)</math> which lies to the right of <math>\left(-\sqrt{24}, 20\right)</math>, which is on the graph <math>y=x^2-4</math>. While technically speaking this doesn't prove that there are no intersections (why?), drawing the graph should convince you that this is the case. Clearly, <math>k<4</math> does not work. | ||
| + | |||
| + | <math>k=5</math> does work because the two graphs intersect at <math>(-5,20)</math>, and by drawing the graph, you realize this is not a tangent point and there is in fact another intersection nearby, due to slope. Therefore, the answer is <math>5+280=\boxed{285}</math>. | ||
| + | |||
| + | *In general (assuming four intersections exist), when two conics intersect, if one conic can be written as <math>ax^2+by^2=f(x,y)</math> and the other as <math>cx^2+dy^2=g(x,y)</math> for polynomials <math>f</math> and <math>g</math> of degree at most <math>1</math>, whenever <math>(a,b),(c,d)</math> are linearly independent (L.I.), we can combine the two equations and then complete the square to achieve <math>(x-p)^2+(y-q)^2=r^2</math>. We can also combine these two equations to form a parabola, or a hyperbola, or an ellipse. When <math>(a,b),(c,d)</math> are not L.I., the intersection points instead lie on a line, which is a circle of radius infinity. When the two conics only have <math>3,2</math> or <math>1</math> intersection point(s), the statement that all these points lie on a circle is trivially true. | ||
| + | |||
| + | ~Ross Gao | ||
| + | |||
| + | ==Solution 3 (Parabola's Properties)== | ||
| + | |||
| + | <i><b>Claim</b></i> | ||
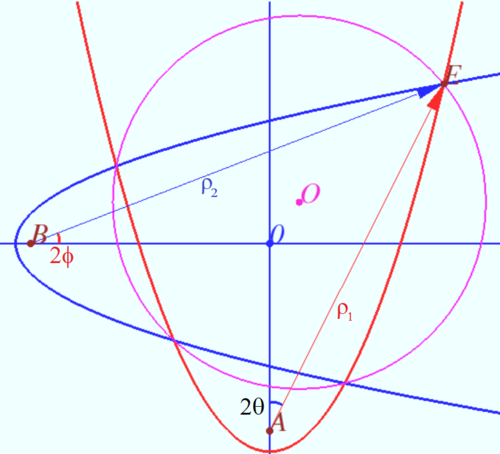
| + | [[File:2021 AIME I 15a.png|500px|right]] | ||
| + | Let the axes of two parabolas be perpendicular, their focal parameters be <math>p_1</math> and <math>p_2</math> and the distances from the foci to the point of intersection of the axes be <math>x_2</math> and <math>y_1</math>. Suppose that these parabolas intersect at four points. | ||
| + | |||
| + | Then these points lie on the circle centered at point <math>(p_2, p_1)</math> with radius <math>r = \sqrt{2(p_1^2 + p_2^2 + p_1 y_1 + p_2 x_2)}.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Let's introduce a coordinate system with the center at the point of intersection of the axes. Let the first (red) parabola have axis <math>x = 0,</math> focal parameter <math>p_1</math> and focus at point <math>A(0, –y_1), y_1 > 0.</math> Let second (blue) parabola have axis <math>y = 0,</math> focal parameter <math>p_2</math> and focus at point <math>B(–x_2,0), x_2 > 0.</math> | ||
| + | Let us denote the angle between the vector connecting the focus of the first parabola and its point and the positive direction of the ordinate axis <math>2\theta,</math> its length <math>\rho_1(\theta),</math> the angle between the vector connecting the focus of the second parabola and its point and the positive direction of the abscissa axis <math>2\phi,</math> its length <math>\rho_2(\phi).</math> Then | ||
| + | <cmath>\rho_1(\theta) = \frac{p_1}{1 - \cos(2\theta)}, \rho_2(\phi) = \frac{p_2}{1 - \cos(2\phi)}.</cmath> | ||
| + | |||
| + | Abscissa of the point of intersection is | ||
| + | <cmath>\begin{align*} x =\rho_1 \sin(2\theta) = p_1\cot\theta = \rho_2 \cos (2\phi) - x_2 = \frac{p_2}{2} (\cot^2\phi - 1)- x_2,\end{align*}</cmath> | ||
| + | <cmath>\begin{align*} x^2 = p_1^2 \cot ^2 \theta , 2 p_1\cot\theta = p_2 \cos^2 \phi - p_2 - 2x_2 .\end{align*}</cmath> | ||
| + | Ordinate of the point of intersection is | ||
| + | <cmath>\begin{align*} y =\rho_2 \sin 2\phi = p_2\cot\phi = \rho_1 \cos 2\theta - y_1 = \frac{p_1}{2} (\cot^2\theta - 1)- y_1,\end{align*}</cmath> | ||
| + | <cmath>\begin{align*} y^2 = p_2^2 \cot ^2 \phi , 2 p_2\cot\phi = p_1 \cos^2 \theta - p_1 - 2y_1 .\end{align*}</cmath> | ||
| + | The square of the distance from point of intersection to the point <math>(p_2, p_1)</math> is | ||
| + | <cmath>\begin{align*} r^2 = (x-p_2)^2 + (y-p_1)^2 = x^2 + y^2 - 2 p_1 y - 2 p_2 x + p_1^2 + p_2^2 .\end{align*}</cmath> | ||
| + | After simple transformations, we get <math>r^2 = 2(p_1^2 + p_2^2 + p_1 y_1 + p_2 x_2).</math> | ||
| + | |||
| + | Hence, any intersection point has the same distance <math>r</math> from the point <math>(p_2, p_1).</math> | ||
| − | |||
| − | + | <i><b>Solution</b></i> | |
| − | <math> | + | Parameters of the parabola <math>y = x^2 – k</math> are <math>p_1 = \frac{1}{2}, y_1 = 20 + k – \frac{1}{2}.</math> |
| − | <math> | + | Parameters of the parabola <math>\frac{x}{2} = (y – 20)^2 – \frac{k}{2}</math> are <math>p_2 = \frac{1}{4}, x_2 = k – \frac{1}{4} \implies |
| + | r^2 = 20 + \frac{3k}{2}.</math> | ||
| + | If <math>r \le 21, k \le \frac{842}{3},</math> then integer <math>k \le 280.</math> | ||
| − | + | The vertex of the second parabola is point <math>(– k,20)</math> can be on the parabola <math>y = x^2 – k</math> or below the point of the parabola with the same abscissa. So <cmath>20 \ge (– k)^2 – k \implies 5 \le k \le 280.</cmath> Therefore, the answer is <math>5+280=\boxed{285}</math>. | |
| − | + | '''vladimir.shelomovskii@gmail.com, vvsss''' | |
| − | ==See | + | ==See Also== |
{{AIME box|year=2021|n=I|num-b=14|after=Last problem}} | {{AIME box|year=2021|n=I|num-b=14|after=Last problem}} | ||
[[Category:Intermediate Algebra Problems]] | [[Category:Intermediate Algebra Problems]] | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 02:31, 13 November 2023
Contents
Problem
Let ![]() be the set of positive integers
be the set of positive integers ![]() such that the two parabolas
such that the two parabolas![]() intersect in four distinct points, and these four points lie on a circle with radius at most
intersect in four distinct points, and these four points lie on a circle with radius at most ![]() . Find the sum of the least element of
. Find the sum of the least element of ![]() and the greatest element of
and the greatest element of ![]() .
.
Diagram
Graph in Desmos: https://www.desmos.com/calculator/37hsgxbygj
~MRENTHUSIASM
Solution 1 (Inequalities and Circles)
Note that ![]() is an upward-opening parabola with the vertex at
is an upward-opening parabola with the vertex at ![]() and
and ![]() is a rightward-opening parabola with the vertex at
is a rightward-opening parabola with the vertex at ![]() We consider each condition separately:
We consider each condition separately:
- The two parabolas intersect at four distinct points.
- The point
 is on or below the parabola
is on or below the parabola 
We need
 from which
from which 
Moreover, the point
 is on the parabola
is on the parabola  when
when  We will prove that the two parabolas intersect at four distinct points at this value of
We will prove that the two parabolas intersect at four distinct points at this value of 
Substituting
 into
into  we get
we get  Expanding and rearranging give
Expanding and rearranging give ![\[2x^4-100x^2-x+1245=0. \hspace{20mm}(\bigstar)\]](//latex.artofproblemsolving.com/8/5/3/853de6596321303a7da52ab11b267ad929e466cd.png) By either the graphs of the parabolas or the Rational Root Theorem, we conclude that
By either the graphs of the parabolas or the Rational Root Theorem, we conclude that  is a root of
is a root of  So, we factor its left side:
So, we factor its left side: ![\[(x+5)\left(2x^3-10x^2-50x+249\right)=0.\]](//latex.artofproblemsolving.com/2/e/1/2e1fb0f019fbd6e1520acd65a356b18fc152d53f.png) By either the graphs of the parabolas or Descartes' Rule of Signs, we conclude that
By either the graphs of the parabolas or Descartes' Rule of Signs, we conclude that  has two positive roots and one negative root such that
has two positive roots and one negative root such that  So,
So,  has four distinct real roots, or the two parabolas intersect at four distinct points.
has four distinct real roots, or the two parabolas intersect at four distinct points.For Subcondition A, we deduce that

Remark for Subcondition A
Recall that if
 then the point
then the point  is above the parabola
is above the parabola  It follows that for
It follows that for 
- The maximum value of
 for the parabola
for the parabola  occurs at
occurs at  from which
from which 
- The minimum value of
 for the parabola
for the parabola  occurs at
occurs at  from which
from which 
Clearly, the parabola
 and the left half of the parabola
and the left half of the parabola  do not intersect. Therefore, the two parabolas do not intersect at four distinct points.
do not intersect. Therefore, the two parabolas do not intersect at four distinct points.
- The maximum value of
- The point
 is on or below the parabola
is on or below the parabola 
The lower half of the parabola
 is
is  We need
We need  which holds for all values of
which holds for all values of 
For Subcondition B, we deduce that
 can be any positive integer.
can be any positive integer.
- The four points of intersection lie on a circle with radius at most

For equations of circles, the coefficients of
 and
and  must be the same. So, we add the equation
must be the same. So, we add the equation  to half the equation
to half the equation 
![\[y+\frac12x=x^2+(y-20)^2-\frac32k.\]](//latex.artofproblemsolving.com/d/6/7/d6771fe44c28815130b9929718247b4b28577daa.png) We expand, rearrange, and complete the squares:
We expand, rearrange, and complete the squares:
 We need
We need  from which
from which 
For Condition 2, we obtain

By a quick sketch, we have two subconditions:
For Condition 1, we obtain ![]() by taking the intersection of Subconditions A and B.
by taking the intersection of Subconditions A and B.
Taking the intersection of Conditions 1 and 2 produces ![]() Therefore, the answer is
Therefore, the answer is ![]()
~MRENTHUSIASM
Solution 2 (Translations, Inequalities, Circles)
Make the translation ![]() to obtain
to obtain ![]() and
and ![]() . Multiply the first equation by
. Multiply the first equation by ![]() and sum, we see that
and sum, we see that ![]() . Completing the square gives us
. Completing the square gives us ![]() ; this explains why the two parabolas intersect at four points that lie on a circle*. For the upper bound, observe that
; this explains why the two parabolas intersect at four points that lie on a circle*. For the upper bound, observe that ![]() , so
, so ![]() .
.
For the lower bound, we need to ensure there are ![]() intersections to begin with. (Here I'm using the un-translated coordinates.) Draw up a graph, and realize that two intersections are guaranteed, on the so called "right branch" of
intersections to begin with. (Here I'm using the un-translated coordinates.) Draw up a graph, and realize that two intersections are guaranteed, on the so called "right branch" of ![]() . As we increase the value of
. As we increase the value of ![]() , two more intersections appear on the "left branch":
, two more intersections appear on the "left branch":
![]() does not work because the "leftmost" point of
does not work because the "leftmost" point of ![]() is
is ![]() which lies to the right of
which lies to the right of ![]() , which is on the graph
, which is on the graph ![]() . While technically speaking this doesn't prove that there are no intersections (why?), drawing the graph should convince you that this is the case. Clearly,
. While technically speaking this doesn't prove that there are no intersections (why?), drawing the graph should convince you that this is the case. Clearly, ![]() does not work.
does not work.
![]() does work because the two graphs intersect at
does work because the two graphs intersect at ![]() , and by drawing the graph, you realize this is not a tangent point and there is in fact another intersection nearby, due to slope. Therefore, the answer is
, and by drawing the graph, you realize this is not a tangent point and there is in fact another intersection nearby, due to slope. Therefore, the answer is ![]() .
.
- In general (assuming four intersections exist), when two conics intersect, if one conic can be written as
 and the other as
and the other as  for polynomials
for polynomials  and
and  of degree at most
of degree at most  , whenever
, whenever  are linearly independent (L.I.), we can combine the two equations and then complete the square to achieve
are linearly independent (L.I.), we can combine the two equations and then complete the square to achieve  . We can also combine these two equations to form a parabola, or a hyperbola, or an ellipse. When
. We can also combine these two equations to form a parabola, or a hyperbola, or an ellipse. When  are not L.I., the intersection points instead lie on a line, which is a circle of radius infinity. When the two conics only have
are not L.I., the intersection points instead lie on a line, which is a circle of radius infinity. When the two conics only have  or
or  intersection point(s), the statement that all these points lie on a circle is trivially true.
intersection point(s), the statement that all these points lie on a circle is trivially true.
~Ross Gao
Solution 3 (Parabola's Properties)
Claim
Let the axes of two parabolas be perpendicular, their focal parameters be ![]() and
and ![]() and the distances from the foci to the point of intersection of the axes be
and the distances from the foci to the point of intersection of the axes be ![]() and
and ![]() . Suppose that these parabolas intersect at four points.
. Suppose that these parabolas intersect at four points.
Then these points lie on the circle centered at point ![]() with radius
with radius ![]()
Proof
Let's introduce a coordinate system with the center at the point of intersection of the axes. Let the first (red) parabola have axis ![]() focal parameter
focal parameter ![]() and focus at point
and focus at point ![]() Let second (blue) parabola have axis
Let second (blue) parabola have axis ![]() focal parameter
focal parameter ![]() and focus at point
and focus at point ![]() Let us denote the angle between the vector connecting the focus of the first parabola and its point and the positive direction of the ordinate axis
Let us denote the angle between the vector connecting the focus of the first parabola and its point and the positive direction of the ordinate axis ![]() its length
its length ![]() the angle between the vector connecting the focus of the second parabola and its point and the positive direction of the abscissa axis
the angle between the vector connecting the focus of the second parabola and its point and the positive direction of the abscissa axis ![]() its length
its length ![]() Then
Then
![]()
Abscissa of the point of intersection is
![]()
![]() Ordinate of the point of intersection is
Ordinate of the point of intersection is
![]()
![]() The square of the distance from point of intersection to the point
The square of the distance from point of intersection to the point ![]() is
is
![]() After simple transformations, we get
After simple transformations, we get ![]()
Hence, any intersection point has the same distance ![]() from the point
from the point ![]()
Solution
Parameters of the parabola ![]() are
are ![]()
Parameters of the parabola ![]() are
are ![]()
If ![]() then integer
then integer ![]()
The vertex of the second parabola is point ![]() can be on the parabola
can be on the parabola ![]() or below the point of the parabola with the same abscissa. So
or below the point of the parabola with the same abscissa. So ![]() Therefore, the answer is
Therefore, the answer is ![]() .
.
vladimir.shelomovskii@gmail.com, vvsss
See Also
| 2021 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 





 We need
We need