Difference between revisions of "2021 AIME I Problems/Problem 9"
MRENTHUSIASM (talk | contribs) m (→See also) |
Adam zheng (talk | contribs) (→Solution 10 (Area)) |
||
| (84 intermediate revisions by 12 users not shown) | |||
| Line 3: | Line 3: | ||
==Diagram== | ==Diagram== | ||
| − | + | <asy> | |
| + | /* Made by MRENTHUSIASM */ | ||
| + | size(250); | ||
| + | pair A, B, C, D, E, F, G, H; | ||
| + | A = (-45sqrt(2)/8,18); | ||
| + | B = (45sqrt(2)/8,18); | ||
| + | C = (81sqrt(2)/8,0); | ||
| + | D = (-81sqrt(2)/8,0); | ||
| + | E = foot(A,C,B); | ||
| + | F = foot(A,C,D); | ||
| + | G = foot(A,B,D); | ||
| + | H = intersectionpoint(A--F,B--D); | ||
| + | markscalefactor=0.1; | ||
| + | draw(rightanglemark(A,E,B),red); | ||
| + | draw(rightanglemark(A,F,C),red); | ||
| + | draw(rightanglemark(A,G,D),red); | ||
| + | dot("$A$",A,1.5*NW,linewidth(4)); | ||
| + | dot("$B$",B,1.5*NE,linewidth(4)); | ||
| + | dot("$C$",C,1.5*SE,linewidth(4)); | ||
| + | dot("$D$",D,1.5*SW,linewidth(4)); | ||
| + | dot(E,linewidth(4)); | ||
| + | dot(F,linewidth(4)); | ||
| + | dot(G,linewidth(4)); | ||
| + | draw(A--B--C--D--cycle^^B--D^^B--E); | ||
| + | draw(A--E^^A--F^^A--G,dashed); | ||
| + | label("$10$",midpoint(A--G),1.5*(1,0)); | ||
| + | label("$15$",midpoint(A--E),1.5*N); | ||
| + | Label L = Label("$18$", align=(0,0), position=MidPoint, filltype=Fill(0,3,white)); | ||
| + | draw(C+(5,0)--(81sqrt(2)/8,18)+(5,0), L=L, arrow=Arrows(),bar=Bars(15)); | ||
| + | </asy> | ||
| + | ~MRENTHUSIASM | ||
| − | + | ==Solution 1 (Similar Triangles and Pythagorean Theorem)== | |
| + | Let <math>\overline{AE}, \overline{AF},</math> and <math>\overline{AG}</math> be the perpendiculars from <math>A</math> to <math>\overleftrightarrow{BC}, \overleftrightarrow{CD},</math> and <math>\overleftrightarrow{BD},</math> respectively. Next, let <math>H</math> be the intersection of <math>\overline{AF}</math> and <math>\overline{BD}.</math> | ||
| − | + | We set <math>AB=x</math> and <math>AH=y,</math> as shown below. | |
| − | + | <asy> | |
| + | /* Made by MRENTHUSIASM */ | ||
| + | size(250); | ||
| + | pair A, B, C, D, E, F, G, H; | ||
| + | A = (-45sqrt(2)/8,18); | ||
| + | B = (45sqrt(2)/8,18); | ||
| + | C = (81sqrt(2)/8,0); | ||
| + | D = (-81sqrt(2)/8,0); | ||
| + | E = foot(A,C,B); | ||
| + | F = foot(A,C,D); | ||
| + | G = foot(A,B,D); | ||
| + | H = intersectionpoint(A--F,B--D); | ||
| + | markscalefactor=0.1; | ||
| + | draw(rightanglemark(A,E,B),red); | ||
| + | draw(rightanglemark(A,F,C),red); | ||
| + | draw(rightanglemark(A,G,D),red); | ||
| + | dot("$A$",A,1.5*NW,linewidth(4)); | ||
| + | dot("$B$",B,1.5*NE,linewidth(4)); | ||
| + | dot("$C$",C,1.5*SE,linewidth(4)); | ||
| + | dot("$D$",D,1.5*SW,linewidth(4)); | ||
| + | dot("$E$",E,1.5*dir(E),linewidth(4)); | ||
| + | dot("$F$",F,1.5*S,linewidth(4)); | ||
| + | dot("$G$",G,SE,linewidth(4)); | ||
| + | dot("$H$",H,SE,linewidth(4)); | ||
| + | draw(A--B--C--D--cycle^^B--D^^B--E); | ||
| + | draw(A--E^^A--F^^A--G,dashed); | ||
| + | label("$10$",midpoint(A--G),1.5*(1,0)); | ||
| + | label("$15$",midpoint(A--E),1.5*N); | ||
| + | Label L = Label("$18$", align=(0,0), position=MidPoint, filltype=Fill(0,3,white)); | ||
| + | draw(C+(5,0)--(81sqrt(2)/8,18)+(5,0), L=L, arrow=Arrows(),bar=Bars(15)); | ||
| + | label("$x$",midpoint(A--B),N); | ||
| + | label("$y$",midpoint(A--H),W); | ||
| + | </asy> | ||
| + | From here, we obtain <math>HF=18-y</math> by segment subtraction, and <math>BG=\sqrt{x^2-10^2}</math> and <math>HG=\sqrt{y^2-10^2}</math> by the Pythagorean Theorem. | ||
| − | -- | + | Since <math>\angle ABG</math> and <math>\angle HAG</math> are both complementary to <math>\angle AHB,</math> we have <math>\angle ABG = \angle HAG,</math> from which <math>\triangle ABG \sim \triangle HAG</math> by AA. It follows that <math>\frac{BG}{AG}=\frac{AG}{HG},</math> so <math>BG\cdot HG=AG^2,</math> or <cmath>\sqrt{x^2-10^2}\cdot\sqrt{y^2-10^2}=10^2. \hspace{10mm} (1)</cmath> |
| + | Since <math>\angle AHB = \angle FHD</math> by vertical angles, we have <math>\triangle AHB \sim \triangle FHD</math> by AA, with the ratio of similitude <math>\frac{AH}{FH}=\frac{BA}{DF}.</math> It follows that <math>DF=BA\cdot\frac{FH}{AH}=x\cdot\frac{18-y}{y}.</math> | ||
| − | + | Since <math>\angle EBA = \angle ECD = \angle FDA</math> by angle chasing, we have <math>\triangle EBA \sim \triangle FDA</math> by AA, with the ratio of similitude <math>\frac{EA}{FA}=\frac{BA}{DA}.</math> It follows that <math>DA=BA\cdot\frac{FA}{EA}=x\cdot\frac{18}{15}=\frac{6}{5}x.</math> | |
| − | + | By the Pythagorean Theorem on right <math>\triangle ADF,</math> we have <math>DF^2+AF^2=AD^2,</math> or <cmath>\left(x\cdot\frac{18-y}{y}\right)^2+18^2=\left(\frac{6}{5}x\right)^2. \hspace{7mm} (2)</cmath> | |
| + | Solving this system of equations (<math>(1)</math> and <math>(2)</math>), we get <math>x=\frac{45\sqrt2}{4}</math> and <math>y=\frac{90}{7},</math> so <math>AB=x=\frac{45\sqrt2}{4}</math> and <math>CD=AB+2DF=x+2\left(x\cdot\frac{18-y}{y}\right)=\frac{81\sqrt2}{4}.</math> Finally, the area of <math>ABCD</math> is <cmath>K=\frac{AB+CD}{2}\cdot AF=\frac{567\sqrt2}{2},</cmath> from which <math>\sqrt2 \cdot K=\boxed{567}.</math> | ||
| − | + | ~MRENTHUSIASM | |
| − | + | <u><b>Remark</b></u> | |
| − | + | Instead of solving the system of equations <math>(1)</math> and <math>(2),</math> which can be time consuming, by noting that <math>\triangle ACF \sim \triangle ABG</math> by AA, we could find out <math>\frac{AB}{AG} = \frac{AC}{AF}</math>, which gives <math>AC = \frac{9}{5}x</math>. We also know that <math>EB = \sqrt{x^2 - 15^2}</math> by Pythagorean Theorem on <math>\triangle ABE</math>. From <math>BC = AD = \frac{6}{5}x,</math> we apply the Pythagorean Theorem to <math>\triangle ACE</math> and obtain | |
| + | <cmath>AC^2 = (EB+BC)^2 + AE^2.</cmath> | ||
| + | Substituting, we get | ||
| + | <cmath>\frac{81}{25}x^2 = \left(\sqrt{x^2 -225}+\frac{6}{5}x\right)^2+225 \iff x = 3\sqrt{x^2 - 15^2},</cmath> | ||
| + | from which <math>x = \frac{45\sqrt{2}}{4}.</math> | ||
| − | + | ~Chupdogs | |
| − | + | ==Solution 2 (Similar Triangles and Pythagorean Theorem)== | |
| − | ==Solution 2 ( | ||
| − | |||
| − | |||
| − | == | + | First, draw the diagram. Then, notice that since <math>ABCD</math> is isosceles, <math>\Delta ABD \cong \Delta BAC</math>, and the length of the altitude from <math>B</math> to <math>AC</math> is also <math>10</math>. Let the foot of this altitude be <math>F</math>, and let the foot of the altitude from <math>A</math> to <math>BC</math> be denoted as <math>E</math>. Then, <math>\Delta BCF \sim \Delta ACE</math>. So, <math>\frac{BC}{AC} = \frac{BF}{AE} = \frac{2}{3}</math>. Now, notice that <math>[ABC] = \frac{10 \cdot AC} {2} = \frac{AB \cdot 18}{2} \implies AC = \frac{9 \cdot AB}{5}</math>, where <math>[ABC]</math> denotes the area of triangle <math>ABC</math>. Letting <math>AB = x</math>, this equality becomes <math>AC = \frac{9x}{5}</math>. Also, from <math>\frac{BC}{AC} = \frac{2}{3}</math>, we have <math>BC = \frac{6x}{5}</math>. Now, by the Pythagorean theorem on triangles <math>ABF</math> and <math>CBF</math>, we have <math>AF = \sqrt{x^{2}-100}</math> and <math>CF = \sqrt{ \left( \frac{6x}{5} \right) ^{2}-100}</math>. Notice that <math>AC = AF + CF</math>, so <math>\frac{9x}{5} = \sqrt{x^{2}-100} + \sqrt{ \left( \frac{6x}{5} \right) ^{2}-100}</math>. Squaring both sides of the equation once, moving <math>x^{2}-100</math> and <math> \left( \frac{6x}{5} \right) ^{2}-100</math> to the right, dividing both sides by <math>2</math>, and squaring the equation once more, we are left with <math>\frac{32x^{4}}{25} = 324x^{2}</math>. Dividing both sides by <math>x^{2}</math> (since we know <math>x</math> is positive), we are left with <math>\frac{32x^{2}}{25} = 324</math>. Solving for <math>x</math> gives us <math>x = \frac{45}{2\sqrt{2}}</math>. |
| − | + | ||
| + | Now, let the foot of the perpendicular from <math>A</math> to <math>CD</math> be <math>G</math>. Then let <math>DG = y</math>. Let the foot of the perpendicular from <math>B</math> to <math>CD</math> be <math>H</math>. Then, <math>CH</math> is also equal to <math>y</math>. Notice that <math>ABHG</math> is a rectangle, so <math>GH = x</math>. Now, we have <math>CG = GH + CH = x + y</math>. By the Pythagorean theorem applied to <math>\Delta AGC</math>, we have <math>(x+y)^{2}+18^{2}= \left( \frac{9x}{5} \right) ^{2}</math>. We know that <math>\frac{9x}{5} = \frac{9}{5} \cdot \frac{45}{2\sqrt{2}} = \frac{81}{2\sqrt{2}}</math>, so we can plug this into this equation. Solving for <math>x+y</math>, we get <math>x+y=\frac{63}{2\sqrt{2}}</math>. | ||
| − | + | Finally, to find <math>[ABCD]</math>, we use the formula for the area of a trapezoid: <math>K = [ABCD] = \frac{b_{1}+b_{2}}{2} \cdot h = \frac{AB+CD}{2} \cdot 18 = \frac{x+(CG+DG)}{2} \cdot 18 = \frac{2x+2y}{2} \cdot 18 = (x+y) \cdot 18 = \frac{63}{2\sqrt{2}} \cdot 18 = \frac{567}{\sqrt{2}}</math>. The problem asks us for <math>K \cdot \sqrt{2}</math>, which comes out to be <math>\boxed{567}</math>. | |
| − | + | ~advanture | |
| − | + | ==Solution 3 (Similar Triangles and Pythagorean Theorem)== | |
| + | Make <math>AE</math> perpendicular to <math>BC</math>; <math>AG</math> perpendicular to <math>BD</math>; <math>AF</math> perpendicular <math>DC</math>. | ||
| − | + | It's obvious that <math>\triangle{AEB} \sim \triangle{AFD}</math>. Let <math>EB=5x; AB=5y; DF=6x; AD=6y</math>. Then make <math>BQ</math> perpendicular to <math>DC</math>, it's easy to get <math>BQ=18</math>. | |
| − | + | Since <math>AB</math> parallel to <math>DC</math>, <math>\angle{ABG}=\angle{BDQ}</math>, so <math>\triangle{ABG} \sim \triangle{BDQ}</math>. After drawing the altitude, it's obvious that <math>FQ=AB=5y</math>, so <math>DQ=5y+6x</math>. According to the property of similar triangles, <math>AG/BQ=BG/DQ</math>. So, <math>\frac{5}{9}=\frac{GB}{(6x+5y)}</math>, or <math>GB=\frac{(30x+25y)}{9}</math>. | |
| − | + | Now, we see the <math>\triangle AEB</math>, pretty easy to find that <math>15^2+(5x)^2=(5y)^2</math>, then we get <math>x^2+9=y^2</math>, then express <math>y</math> into <math>x</math> form that <math>y=\sqrt{x^2+9}</math> | |
| + | we put the length of <math>BG</math> back to <math>\triangle AGB</math>: <math>BG^2+100=AB^2</math>. So, <cmath>\frac{[30x+25\sqrt{(x^2+9)}]^2}{81}+100=(5\sqrt{x^2+9})^2.</cmath> | ||
| + | After calculating, we can have a final equation of <math>x^2+9=\sqrt{x^2+9}\cdot3x</math>. It's easy to find <math>x=\frac{3\sqrt{2}}{4}</math> then <math>y=\frac{9\sqrt{2}}{4}</math>. So, <cmath>\sqrt{2}\cdot K = \sqrt{2}\cdot(5y+5y+6x+6x)\cdot9=\boxed{567}.</cmath> | ||
| + | ~bluesoul | ||
| − | ==Solution 4 ( | + | ==Solution 4 (Cyclic Quadrilaterals, Similar Triangles, Pythagorean Theorem)== |
| + | Let the foot of the altitude from <math>A</math> to <math>BC</math> be <math>P</math>, to <math>CD</math> be <math>Q</math>, and to <math>BD</math> be <math>R</math>. | ||
| − | + | Note that all isosceles trapezoids are cyclic quadrilaterals; thus, <math>A</math> is on the circumcircle of <math>\triangle BCD</math> and we have that <math>PRQ</math> is the Simson Line from <math>A</math>. As <math>\angle QAB = 90^\circ</math>, we have that <math>\angle QAR = 90^\circ - \angle RAB =\angle ABR = \angle APR = \angle APQ</math>, with the last equality coming from cyclic quadrilateral <math>APBR</math>. Thus, <math>\triangle QAR \sim \triangle QPA</math> and we have that <math>\frac{AQ}{AR} = \frac{PQ}{PA}</math> or that <math>\frac{18}{10} = \frac{QP}{15}</math>, which we can see gives us that <math>QP = 27</math>. Further ratios using the same similar triangles gives that <math>QR = \frac{25}{3}</math> and <math>RP = \frac{56}{3}</math>. | |
| − | + | We also see that quadrilaterals <math>APBR</math> and <math>ARQD</math> are both cyclic, with diameters of the circumcircles being <math>AB</math> and <math>AD</math> respectively. The intersection of the circumcircles are the points <math>A</math> and <math>R</math>, and we know <math>DRB</math> and <math>QRP</math> are both line segments passing through an intersection of the two circles with one endpoint on each circle. By Fact 5, we know then that there exists a spiral similarity with center <math>A</math> taking <math>\triangle APQ</math> to <math>\triangle APD</math>. Because we know a lot about <math>\triangle APQ</math> but very little about <math>\triangle APD</math> and we would like to know more, we wish to find the ratio of similitude between the two triangles. | |
| − | + | To do this, we use the one number we have for <math>\triangle APD</math>: we know that the altitude from <math>A</math> to <math>BD</math> has length <math>10</math>. As the two triangles are similar, if we can find the height from <math>A</math> to <math>PQ</math>, we can take the ratio of the two heights as the ratio of similitude. To do this, we once again note that <math>QP = 27</math>. Using this, we can drop the altitude from <math>A</math> to <math>QP</math> and let it intersect <math>QP</math> at <math>H</math>. Then, let <math>QH = x</math> and thus <math>HP=27-x</math>. We then have by the Pythagorean Theorem on <math>\triangle AQH</math> and <math>\triangle APH</math>: | |
| + | <cmath>\begin{align*} | ||
| + | 15^2 - x^2 &= 18^2 - (27-x)^2 \\ | ||
| + | 225 - x^2 &= 324 - (x^2-54x+729) \\ | ||
| + | 54x &= 630 \\ | ||
| + | x &= \frac{35}{3}. | ||
| + | \end{align*}</cmath> | ||
| + | Then, <math>RH = QH - QR = \frac{35}{3} - \frac{25}{3} = \frac{10}{3}</math>. This gives us then from right triangle <math>\triangle ARH</math> that <math>AH = \frac{20\sqrt{2}}{3}</math> and thus the ratio of <math>\triangle APQ</math> to <math>\triangle ABD</math> is <math>\frac{3\sqrt{2}}{4}</math>. From this, we see then that <cmath>AB = AP \cdot \frac{3\sqrt{2}}{4} = 15 \cdot \frac{3\sqrt{2}}{4} = \frac{45\sqrt{2}}{4}</cmath> and <cmath>AD = AQ \cdot \frac{3\sqrt{2}}{4} = 18 \cdot \frac{3\sqrt{2}}{4} = \frac{27\sqrt{2}}{2}.</cmath> The Pythagorean Theorem on <math>\triangle AQD</math> then gives that <cmath>QD = \sqrt{AD^2 - AQ^2} = \sqrt{\left(\frac{27\sqrt{2}}{2}\right)^2 - 18^2} = \sqrt{\frac{81}{2}} = \frac{9\sqrt{2}}{2}.</cmath> | ||
| + | Then, we have the height of trapezoid <math>ABCD</math> is <math>AQ = 18</math>, the top base is <math>AB = \frac{45\sqrt{2}}{4}</math>, and the bottom base is <math>CD = \frac{45\sqrt{2}}{4} + 2\cdot\frac{9\sqrt{2}}{2}</math>. From the equation of a trapezoid, <math>K = \frac{b_1+b_2}{2} \cdot h = \frac{63\sqrt{2}}{4} \cdot 18 = \frac{567\sqrt{2}}{2}</math>, so the answer is <math>K\sqrt{2} = \boxed{567}</math>. | ||
| − | ~ | + | ~lvmath |
| − | ==Solution 5 ( | + | ==Solution 5 (Cyclic Quadrilaterals, Similar Triangles, Pythagorean Theorem)== |
Let <math>E,F,</math> and <math>G</math> be the feet of the altitudes from <math>A</math> to <math>BC,CD,</math> and <math>DB</math>, respectively. | Let <math>E,F,</math> and <math>G</math> be the feet of the altitudes from <math>A</math> to <math>BC,CD,</math> and <math>DB</math>, respectively. | ||
| Line 60: | Line 141: | ||
Claim: We have <math>2</math> pairs of similar right triangles: <math>\triangle AEB \sim \triangle AFD</math> and <math>\triangle AGD \sim \triangle AEC</math>. | Claim: We have <math>2</math> pairs of similar right triangles: <math>\triangle AEB \sim \triangle AFD</math> and <math>\triangle AGD \sim \triangle AEC</math>. | ||
| − | Proof: Note that <math>ABCD</math> is cyclic. We need one more angle, and we get this from this cyclic | + | Proof: Note that <math>ABCD</math> is cyclic. We need one more angle, and we get this from this cyclic quadrilateral: |
| − | + | <cmath>\begin{align*} | |
| − | + | \angle ABE &= 180^\circ - \angle ABC =\angle ADC = \angle ADG, \\ | |
| + | \angle ADG &= \angle ADB =\angle ACB = \angle ACE. \hspace{20mm} \square | ||
| + | \end{align*}</cmath> | ||
Let <math>AD=a</math>. We obtain from the similarities <math>AB = \frac{5a}{6}</math> and <math>AC=BD=\frac{3a}{2}</math>. | Let <math>AD=a</math>. We obtain from the similarities <math>AB = \frac{5a}{6}</math> and <math>AC=BD=\frac{3a}{2}</math>. | ||
| − | By Ptolemy, <math>(\frac{3a}{2})^2 = a^2 + \frac{5a}{6} \cdot CD</math>, so <math>\frac{5a^2}{4} = \frac{5a}{6} \cdot CD</math>. | + | By Ptolemy, <math>\left(\frac{3a}{2}\right)^2 = a^2 + \frac{5a}{6} \cdot CD</math>, so <math>\frac{5a^2}{4} = \frac{5a}{6} \cdot CD</math>. |
We obtain <math>CD=\frac{3a}{2}</math>, so <math>DF=\frac{CD-AB}{2}=\frac{a}{3}</math>. | We obtain <math>CD=\frac{3a}{2}</math>, so <math>DF=\frac{CD-AB}{2}=\frac{a}{3}</math>. | ||
| Line 71: | Line 154: | ||
Applying the Pythagorean theorem on <math>\triangle ADF</math>, we get <math>324=a^2 - \frac{a^2}{9}=\frac{8a^2}{9}</math>. | Applying the Pythagorean theorem on <math>\triangle ADF</math>, we get <math>324=a^2 - \frac{a^2}{9}=\frac{8a^2}{9}</math>. | ||
| − | Thus, <math>a=\frac{27}{\sqrt{2}}</math>, and <math>[ABCD]=\frac{AB+CD}{2} \cdot 18 = \frac{\frac{5a}{6} +\frac{9a}{6}}{2} \cdot 18 = 18 \cdot \frac{7}{6} \cdot \frac{27}{\sqrt{2}} = \frac{567}{\sqrt{2}}</math>, yielding <math>\boxed{567}</math>. | + | Thus, <math>a=\frac{27}{\sqrt{2}}</math>, and <math>[ABCD]=\frac{AB+CD}{2} \cdot 18 = \frac{\frac{5a}{6} +\frac{9a}{6}}{2} \cdot 18 = 18 \cdot \frac{7}{6} \cdot \frac{27}{\sqrt{2}} = \frac{567}{\sqrt{2}}</math>, yielding <math>\sqrt2\cdot[ABCD]=\boxed{567}</math>. |
| + | |||
| + | ==Solution 6 (Similar Triangles and Trigonometry)== | ||
| + | Let <math>AD=BC=a</math>. Draw diagonal <math>AC</math> and let <math>G</math> be the foot of the perpendicular from <math>B</math> to <math>AC</math>, <math>F</math> be the foot of the perpendicular from <math>A</math> to line <math>BC</math>, and <math>H</math> be the foot of the perpendicular from <math>A</math> to <math>DC</math>. | ||
| + | |||
| + | Note that <math>\triangle CBG\sim\triangle CAF</math>, and we get that <math>\frac{10}{15}=\frac{a}{AC}</math>. Therefore, <math>AC=\frac32 a</math>. It then follows that <math>\triangle ABF\sim\triangle ADH</math>. Using similar triangles, we can then find that <math>AB=\frac{5}{6}a</math>. Using the Law of Cosines on <math>\triangle ABC</math>, We can find that the <math>\cos\angle ABC=-\frac{1}{3}</math>. Since <math>\angle ABF=\angle ADH</math>, and each is supplementary to <math>\angle ABC</math>, we know that the <math>\cos\angle ADH=\frac{1}{3}</math>. It then follows that <math>a=\frac{27\sqrt{2}}{2}</math>. Then it can be found that the area <math>K</math> is <math>\frac{567\sqrt{2}}{2}</math>. Multiplying this by <math>\sqrt{2}</math>, the answer is <math>\boxed{567}</math>. | ||
| + | |||
| + | ~happykeeper | ||
| + | |||
| + | ==Solution 7 (Similar Triangles and Trigonometry)== | ||
| + | Draw the distances in terms of <math>B</math>, as shown in the diagram. By similar triangles, <math>\triangle{AEC}\sim\triangle{BIC}</math>. As a result, let <math>AB=u</math>, then <math>BC=AD=\frac{6}{5}u</math> and <math>2AC=3BC</math>. The triangle <math>ABC</math> is <math>6-5-9</math> which <math>\cos(\angle{ABC})=-\frac{1}{3}</math>. By angle subtraction, <math>\cos(180-\theta)=-\cos\theta</math>. Therefore, <math>AB=\frac{45}{2\sqrt{2}}=\frac{45\sqrt{2}}{4}</math> and <math>AD=BC=\frac{27}{\sqrt{2}}</math>. By trapezoid area formula, the area of <math>ABCD</math> is equal to <math>(AB+DF)\cdot 18=567\cdot \frac{\sqrt{2}}{2}</math> which <math>\sqrt{2}\cdot k=\boxed{567}</math>. | ||
| + | |||
| + | ~math2718281828459 | ||
| + | |||
| + | ==Solution 8 (Heron's Formula)== | ||
| + | <asy> | ||
| + | size(250); | ||
| + | pair A, B, C, D, E, F, G, H; | ||
| + | A = (-45sqrt(2)/8,18); | ||
| + | B = (45sqrt(2)/8,18); | ||
| + | C = (81sqrt(2)/8,0); | ||
| + | D = (-81sqrt(2)/8,0); | ||
| + | E = foot(A,C,B); | ||
| + | F = foot(A,C,D); | ||
| + | G = foot(A,B,D); | ||
| + | H = intersectionpoint(A--F,B--D); | ||
| + | markscalefactor=0.1; | ||
| + | draw(rightanglemark(A,E,B),red); | ||
| + | draw(rightanglemark(A,F,C),red); | ||
| + | draw(rightanglemark(A,G,D),red); | ||
| + | filldraw(A--D--F--cycle,yellow,black+linewidth(1.5)); | ||
| + | filldraw(A--B--E--cycle,yellow,black+linewidth(1.5)); | ||
| + | dot("$A$",A,1.5*NW,linewidth(4)); | ||
| + | dot("$B$",B,1.5*NE,linewidth(4)); | ||
| + | dot("$C$",C,1.5*SE,linewidth(4)); | ||
| + | dot("$D$",D,1.5*SW,linewidth(4)); | ||
| + | dot(E,linewidth(4)); | ||
| + | dot(F,linewidth(4)); | ||
| + | dot(G,linewidth(4)); | ||
| + | label("$E$",E,NE); | ||
| + | label("$F$",F, S); | ||
| + | label("$G$",G,SE); | ||
| + | draw(A--B--C--D--cycle^^B--D^^B--E); | ||
| + | draw(A--E^^A--F^^A--G,dashed); | ||
| + | label("$10$",midpoint(A--G),1.5*(1,0)); | ||
| + | label("$15$",midpoint(A--E),1.5*N); | ||
| + | label("$5x$",midpoint(A--B),S); | ||
| + | label("$6x$",midpoint(A--D),1.5*(-1,0)); | ||
| + | Label L = Label("$18$", align=(0,0), position=MidPoint, filltype=Fill(0,3,white)); | ||
| + | draw(C+(5,0)--(81sqrt(2)/8,18)+(5,0), L=L, arrow=Arrows(),bar=Bars(15)); | ||
| + | </asy> | ||
| + | Let the points formed by dropping altitudes from <math>A</math> to the lines <math>BC</math>, <math>CD</math>, and <math>BD</math> be <math>E</math>, <math>F</math>, and <math>G</math>, respectively. | ||
| + | |||
| + | We have | ||
| + | <cmath>\triangle ABE \sim \triangle ADF \implies \frac{AD}{18} = \frac{AB}{15} \implies AD = \frac{6}{5}AB</cmath> | ||
| + | and | ||
| + | <cmath>BD\cdot10 = 2[ABD] = AB\cdot18 \implies BD = \frac{9}{5}AB.</cmath> | ||
| + | For convenience, let <math>AB = 5x</math>. By Heron's formula on <math>\triangle ABD</math>, we have sides <math>5x,6x,9x</math> and semiperimeter <math>10x</math>, so | ||
| + | <cmath>\sqrt{10x\cdot5x\cdot4x\cdot1x} = [ABD] = \frac{AB\cdot18}{2} = 45x \implies 10\sqrt{2}x^2 = 45x \implies x= \frac{45}{10\sqrt{2}},</cmath> | ||
| + | so <math>AB = 5x = \frac{45}{2\sqrt{2}}</math>. | ||
| + | |||
| + | Then, | ||
| + | <cmath>BE = \sqrt{AB^2 - CA^2} = \sqrt{\left(\frac{45}{2\sqrt{2}}\right)^2 - 15^2} = \sqrt{\frac{225}{8}} = \frac{15}{2\sqrt{2}}</cmath> | ||
| + | and | ||
| + | <cmath>\triangle ABE \sim \triangle ADF \implies DF = \frac{6}{5}BE = \frac{6}{5}\cdot\frac{15}{2\sqrt{2}} = \frac{18}{2\sqrt{2}}.</cmath> | ||
| + | Finally, recalling that <math>ABCD</math> is isosceles, | ||
| + | <cmath>K = [ABCD] = \frac{18}{2}(AB + (AB + 2DF)) = 18(AB + DF) = 18\left(\frac{45}{2\sqrt{2}} + \frac{18}{2\sqrt{2}}\right) = \frac{567}{\sqrt{2}},</cmath> | ||
| + | so <math>\sqrt{2}\cdot K = \boxed{567}</math>. | ||
| + | |||
| + | ~[[User:emerald_block|emerald_block]] | ||
| + | |||
| + | ==Solution 9 (Three Heights)== | ||
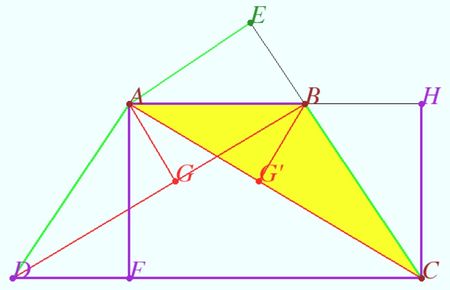
| + | [[File:2021 AIME I 9.jpg|450px|right]] | ||
| + | |||
| + | Let <math>\overline{AE}, \overline{AF},</math> and <math>\overline{AG}</math> be the perpendiculars from <math>A</math> to <math>{BC}, {CD},</math> and <math>{BD},</math> respectively. | ||
| + | <math>AE = 15, AF = 18, AG =10</math>. | ||
| + | Denote by <math>G'</math> the base of the perpendicular from <math>B</math> to <math>AC, H</math> be the base of the perpendicular from <math>C</math> to <math>AB</math>. Denote <math>\theta = \angle{CBH}.</math> | ||
| + | It is clear that <cmath>BG' = AG, CH = AF, \triangle CBH \ =\triangle ADF,</cmath> the area of <math>ABCD</math> is equal to the area of the rectangle <math>AFCH.</math> | ||
| + | |||
| + | The problem is reduced to finding <math>AH</math>. | ||
| + | |||
| + | In triangle <math>ABC</math> all altitudes are known: | ||
| + | <cmath>AB : BC : AC = \frac{1}{CH}\ : \frac{1}{AE}\ : \frac{1}{BG'}\ =</cmath> | ||
| + | <cmath>= \frac{1}{AF}\ : \frac{1}{AE}\ : \frac{1}{AG}\ = 5 : 6 : 9.</cmath> | ||
| + | We apply the Law of Cosines to <math>\triangle ABC</math> and get<math>:</math> | ||
| + | <cmath>\begin{align*} 2\cdot AB\cdot BC \cdot \cos\theta = AC^2 – AB^2 – BC^2, \end{align*}</cmath> | ||
| + | <cmath>\begin{align*} 2\cdot 5\cdot 6\cdot \cos\theta = 60 \cos\theta = 9^2 – 5^2 – 6^2 = 20, \cos\theta =\frac{1}{3}. \end{align*}</cmath> | ||
| + | <cmath>\begin{align*} BH = BC \cos\theta = \frac{BC}{3}.\end{align*}</cmath> | ||
| + | We apply the Pythagorean Law to <math>\triangle HBC</math> and get<math>:</math> | ||
| + | <cmath>\begin{align*} HC^2 = 18^2 = BC^2 – BH^2 = 9\cdot BH^2 – BH^2 = 8 BH^2.\end{align*}</cmath> | ||
| + | <cmath>\begin{align*} BH = \frac{9}{\sqrt2}, AH = (\frac{5}{2} + 1)\cdot BH = \frac{63}{2\cdot \sqrt2}. \end{align*}</cmath> | ||
| + | Required area is | ||
| + | <cmath>\begin{align*} K = \frac{63}{2\cdot \sqrt{2}} \cdot 18 = \frac{567}{\sqrt{2}} \implies \sqrt{2} K=\boxed{567}. \end{align*}</cmath> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Solution 10 (Area)== | ||
| + | Let <math>F</math> be on <math>DC</math> such that <math>AF \| DC</math>. Let <math>G</math> be on <math>BD</math> such that <math>AG \| BD</math>. | ||
| + | |||
| + | Let <math>m</math> be the length of <math>AB</math>. Let <math>n</math> be the length of <math>AD</math>. | ||
| + | |||
| + | The area of <math>\triangle ABD</math> can be expressed in three ways: <math>\frac{1}{2}(15)(BC) = \frac{1}{2}(15)(n)</math>, <math>\frac{1}{2}(18)(m)</math>, and <math>\frac{1}{2}(10)(BD)</math>. | ||
| − | + | <cmath> | |
| − | + | \frac{1}{2}(15)(n) = \frac{1}{2}(18)(m) | |
| + | </cmath> | ||
| + | <cmath> | ||
| + | 15n = 18m | ||
| + | </cmath> | ||
| + | <cmath> | ||
| + | 5n = 6m | ||
| + | </cmath> | ||
| + | <cmath> | ||
| + | n = \frac{6}{5}m | ||
| + | </cmath> | ||
| − | + | Now, <math>BD = BG + GD = \sqrt{m^2-100} + \sqrt{n^2-100}</math>. We can substitute in <math>n = \frac{6}{5}m</math> to get | |
| − | + | <math>BD = \sqrt{m^2-100} + \sqrt{(\frac{6}{5}m)^2-100}</math>. | |
| − | + | We have | |
| + | <cmath> | ||
| + | \frac{1}{2}(10)\left(\sqrt{m^2-100} + \sqrt{(\frac{6}{5}m)^2-100}\right) = \frac{1}{2}(18)(m) | ||
| + | </cmath> | ||
| + | After a fairly straightforward algebraic bash, we get <math>m = \frac{45\sqrt{2}}{4}</math>, and <math>n = (\frac{6}{5})(\frac{45\sqrt{2}}{4}) = \frac{27\sqrt{2}}{2}</math>. By the Pythagorean Theorem on <math>\triangle ADF</math>, <math>DF^2 = n^2 - 18^2 = \frac{729}{2} - 324 = \frac{81}{2}</math>, and <math>DF = \frac{9\sqrt{2}}{2}</math>. | ||
| − | + | Thus, <math>DC = 2DF + AB = 9\sqrt{2}+\frac{45\sqrt{2}}{4} = \frac{81\sqrt{2}}{4}</math>. Therefore, <math>K = \frac{1}{2}(\frac{45\sqrt{2}}{4}+\frac{81\sqrt{2}}{4}) \cdot 18 = \frac{63\sqrt{2}}{2} \cdot 18 = \frac{567\sqrt{2}}{2}</math>. The requested answer is <math>K \cdot \sqrt{2} = \boxed{567}</math>. | |
| − | |||
| − | + | ~ adam_zheng | |
| − | + | ==Video Solution== | |
| − | + | https://youtu.be/uItEKVj-tF8 | |
| − | ~ | + | ~Mathproblemsolvingskills.com |
==Video Solution== | ==Video Solution== | ||
Latest revision as of 18:16, 25 January 2024
Contents
- 1 Problem
- 2 Diagram
- 3 Solution 1 (Similar Triangles and Pythagorean Theorem)
- 4 Solution 2 (Similar Triangles and Pythagorean Theorem)
- 5 Solution 3 (Similar Triangles and Pythagorean Theorem)
- 6 Solution 4 (Cyclic Quadrilaterals, Similar Triangles, Pythagorean Theorem)
- 7 Solution 5 (Cyclic Quadrilaterals, Similar Triangles, Pythagorean Theorem)
- 8 Solution 6 (Similar Triangles and Trigonometry)
- 9 Solution 7 (Similar Triangles and Trigonometry)
- 10 Solution 8 (Heron's Formula)
- 11 Solution 9 (Three Heights)
- 12 Solution 10 (Area)
- 13 Video Solution
- 14 Video Solution
- 15 See Also
Problem
Let ![]() be an isosceles trapezoid with
be an isosceles trapezoid with ![]() and
and ![]() Suppose that the distances from
Suppose that the distances from ![]() to the lines
to the lines ![]() and
and ![]() are
are ![]() and
and ![]() respectively. Let
respectively. Let ![]() be the area of
be the area of ![]() Find
Find ![]()
Diagram
![[asy] /* Made by MRENTHUSIASM */ size(250); pair A, B, C, D, E, F, G, H; A = (-45sqrt(2)/8,18); B = (45sqrt(2)/8,18); C = (81sqrt(2)/8,0); D = (-81sqrt(2)/8,0); E = foot(A,C,B); F = foot(A,C,D); G = foot(A,B,D); H = intersectionpoint(A--F,B--D); markscalefactor=0.1; draw(rightanglemark(A,E,B),red); draw(rightanglemark(A,F,C),red); draw(rightanglemark(A,G,D),red); dot("$A$",A,1.5*NW,linewidth(4)); dot("$B$",B,1.5*NE,linewidth(4)); dot("$C$",C,1.5*SE,linewidth(4)); dot("$D$",D,1.5*SW,linewidth(4)); dot(E,linewidth(4)); dot(F,linewidth(4)); dot(G,linewidth(4)); draw(A--B--C--D--cycle^^B--D^^B--E); draw(A--E^^A--F^^A--G,dashed); label("$10$",midpoint(A--G),1.5*(1,0)); label("$15$",midpoint(A--E),1.5*N); Label L = Label("$18$", align=(0,0), position=MidPoint, filltype=Fill(0,3,white)); draw(C+(5,0)--(81sqrt(2)/8,18)+(5,0), L=L, arrow=Arrows(),bar=Bars(15)); [/asy]](http://latex.artofproblemsolving.com/3/a/b/3abb81a1ad3a9d71de8b1addf0d3fae441b6afb1.png) ~MRENTHUSIASM
~MRENTHUSIASM
Solution 1 (Similar Triangles and Pythagorean Theorem)
Let ![]() and
and ![]() be the perpendiculars from
be the perpendiculars from ![]() to
to ![]() and
and ![]() respectively. Next, let
respectively. Next, let ![]() be the intersection of
be the intersection of ![]() and
and ![]()
We set ![]() and
and ![]() as shown below.
as shown below.
![[asy] /* Made by MRENTHUSIASM */ size(250); pair A, B, C, D, E, F, G, H; A = (-45sqrt(2)/8,18); B = (45sqrt(2)/8,18); C = (81sqrt(2)/8,0); D = (-81sqrt(2)/8,0); E = foot(A,C,B); F = foot(A,C,D); G = foot(A,B,D); H = intersectionpoint(A--F,B--D); markscalefactor=0.1; draw(rightanglemark(A,E,B),red); draw(rightanglemark(A,F,C),red); draw(rightanglemark(A,G,D),red); dot("$A$",A,1.5*NW,linewidth(4)); dot("$B$",B,1.5*NE,linewidth(4)); dot("$C$",C,1.5*SE,linewidth(4)); dot("$D$",D,1.5*SW,linewidth(4)); dot("$E$",E,1.5*dir(E),linewidth(4)); dot("$F$",F,1.5*S,linewidth(4)); dot("$G$",G,SE,linewidth(4)); dot("$H$",H,SE,linewidth(4)); draw(A--B--C--D--cycle^^B--D^^B--E); draw(A--E^^A--F^^A--G,dashed); label("$10$",midpoint(A--G),1.5*(1,0)); label("$15$",midpoint(A--E),1.5*N); Label L = Label("$18$", align=(0,0), position=MidPoint, filltype=Fill(0,3,white)); draw(C+(5,0)--(81sqrt(2)/8,18)+(5,0), L=L, arrow=Arrows(),bar=Bars(15)); label("$x$",midpoint(A--B),N); label("$y$",midpoint(A--H),W); [/asy]](http://latex.artofproblemsolving.com/0/9/c/09c88c08fcd03662bd60e81e7b02146c129e2bf6.png) From here, we obtain
From here, we obtain ![]() by segment subtraction, and
by segment subtraction, and ![]() and
and ![]() by the Pythagorean Theorem.
by the Pythagorean Theorem.
Since ![]() and
and ![]() are both complementary to
are both complementary to ![]() we have
we have ![]() from which
from which ![]() by AA. It follows that
by AA. It follows that ![]() so
so ![]() or
or ![]() Since
Since ![]() by vertical angles, we have
by vertical angles, we have ![]() by AA, with the ratio of similitude
by AA, with the ratio of similitude ![]() It follows that
It follows that ![]()
Since ![]() by angle chasing, we have
by angle chasing, we have ![]() by AA, with the ratio of similitude
by AA, with the ratio of similitude ![]() It follows that
It follows that ![]()
By the Pythagorean Theorem on right ![]() we have
we have ![]() or
or ![]() Solving this system of equations (
Solving this system of equations (![]() and
and ![]() ), we get
), we get ![]() and
and ![]() so
so ![]() and
and ![]() Finally, the area of
Finally, the area of ![]() is
is ![]() from which
from which ![]()
~MRENTHUSIASM
Remark
Instead of solving the system of equations ![]() and
and ![]() which can be time consuming, by noting that
which can be time consuming, by noting that ![]() by AA, we could find out
by AA, we could find out ![]() , which gives
, which gives ![]() . We also know that
. We also know that ![]() by Pythagorean Theorem on
by Pythagorean Theorem on ![]() . From
. From ![]() we apply the Pythagorean Theorem to
we apply the Pythagorean Theorem to ![]() and obtain
and obtain
![]() Substituting, we get
Substituting, we get
![]() from which
from which ![]()
~Chupdogs
Solution 2 (Similar Triangles and Pythagorean Theorem)
First, draw the diagram. Then, notice that since ![]() is isosceles,
is isosceles, ![]() , and the length of the altitude from
, and the length of the altitude from ![]() to
to ![]() is also
is also ![]() . Let the foot of this altitude be
. Let the foot of this altitude be ![]() , and let the foot of the altitude from
, and let the foot of the altitude from ![]() to
to ![]() be denoted as
be denoted as ![]() . Then,
. Then, ![]() . So,
. So, ![]() . Now, notice that
. Now, notice that ![]() , where
, where ![]() denotes the area of triangle
denotes the area of triangle ![]() . Letting
. Letting ![]() , this equality becomes
, this equality becomes ![]() . Also, from
. Also, from ![]() , we have
, we have ![]() . Now, by the Pythagorean theorem on triangles
. Now, by the Pythagorean theorem on triangles ![]() and
and ![]() , we have
, we have ![]() and
and  . Notice that
. Notice that ![]() , so
, so  . Squaring both sides of the equation once, moving
. Squaring both sides of the equation once, moving ![]() and
and ![]() to the right, dividing both sides by
to the right, dividing both sides by ![]() , and squaring the equation once more, we are left with
, and squaring the equation once more, we are left with ![]() . Dividing both sides by
. Dividing both sides by ![]() (since we know
(since we know ![]() is positive), we are left with
is positive), we are left with ![]() . Solving for
. Solving for ![]() gives us
gives us ![]() .
.
Now, let the foot of the perpendicular from ![]() to
to ![]() be
be ![]() . Then let
. Then let ![]() . Let the foot of the perpendicular from
. Let the foot of the perpendicular from ![]() to
to ![]() be
be ![]() . Then,
. Then, ![]() is also equal to
is also equal to ![]() . Notice that
. Notice that ![]() is a rectangle, so
is a rectangle, so ![]() . Now, we have
. Now, we have ![]() . By the Pythagorean theorem applied to
. By the Pythagorean theorem applied to ![]() , we have
, we have ![]() . We know that
. We know that ![]() , so we can plug this into this equation. Solving for
, so we can plug this into this equation. Solving for ![]() , we get
, we get ![]() .
.
Finally, to find ![]() , we use the formula for the area of a trapezoid:
, we use the formula for the area of a trapezoid: ![]() . The problem asks us for
. The problem asks us for ![]() , which comes out to be
, which comes out to be ![]() .
.
~advanture
Solution 3 (Similar Triangles and Pythagorean Theorem)
Make ![]() perpendicular to
perpendicular to ![]() ;
; ![]() perpendicular to
perpendicular to ![]() ;
; ![]() perpendicular
perpendicular ![]() .
.
It's obvious that ![]() . Let
. Let ![]() . Then make
. Then make ![]() perpendicular to
perpendicular to ![]() , it's easy to get
, it's easy to get ![]() .
.
Since ![]() parallel to
parallel to ![]() ,
, ![]() , so
, so ![]() . After drawing the altitude, it's obvious that
. After drawing the altitude, it's obvious that ![]() , so
, so ![]() . According to the property of similar triangles,
. According to the property of similar triangles, ![]() . So,
. So, ![]() , or
, or ![]() .
.
Now, we see the ![]() , pretty easy to find that
, pretty easy to find that ![]() , then we get
, then we get ![]() , then express
, then express ![]() into
into ![]() form that
form that ![]() we put the length of
we put the length of ![]() back to
back to ![]() :
: ![]() . So,
. So, ![]() After calculating, we can have a final equation of
After calculating, we can have a final equation of ![]() . It's easy to find
. It's easy to find ![]() then
then ![]() . So,
. So, ![]() ~bluesoul
~bluesoul
Solution 4 (Cyclic Quadrilaterals, Similar Triangles, Pythagorean Theorem)
Let the foot of the altitude from ![]() to
to ![]() be
be ![]() , to
, to ![]() be
be ![]() , and to
, and to ![]() be
be ![]() .
.
Note that all isosceles trapezoids are cyclic quadrilaterals; thus, ![]() is on the circumcircle of
is on the circumcircle of ![]() and we have that
and we have that ![]() is the Simson Line from
is the Simson Line from ![]() . As
. As ![]() , we have that
, we have that ![]() , with the last equality coming from cyclic quadrilateral
, with the last equality coming from cyclic quadrilateral ![]() . Thus,
. Thus, ![]() and we have that
and we have that ![]() or that
or that ![]() , which we can see gives us that
, which we can see gives us that ![]() . Further ratios using the same similar triangles gives that
. Further ratios using the same similar triangles gives that ![]() and
and ![]() .
.
We also see that quadrilaterals ![]() and
and ![]() are both cyclic, with diameters of the circumcircles being
are both cyclic, with diameters of the circumcircles being ![]() and
and ![]() respectively. The intersection of the circumcircles are the points
respectively. The intersection of the circumcircles are the points ![]() and
and ![]() , and we know
, and we know ![]() and
and ![]() are both line segments passing through an intersection of the two circles with one endpoint on each circle. By Fact 5, we know then that there exists a spiral similarity with center
are both line segments passing through an intersection of the two circles with one endpoint on each circle. By Fact 5, we know then that there exists a spiral similarity with center ![]() taking
taking ![]() to
to ![]() . Because we know a lot about
. Because we know a lot about ![]() but very little about
but very little about ![]() and we would like to know more, we wish to find the ratio of similitude between the two triangles.
and we would like to know more, we wish to find the ratio of similitude between the two triangles.
To do this, we use the one number we have for ![]() : we know that the altitude from
: we know that the altitude from ![]() to
to ![]() has length
has length ![]() . As the two triangles are similar, if we can find the height from
. As the two triangles are similar, if we can find the height from ![]() to
to ![]() , we can take the ratio of the two heights as the ratio of similitude. To do this, we once again note that
, we can take the ratio of the two heights as the ratio of similitude. To do this, we once again note that ![]() . Using this, we can drop the altitude from
. Using this, we can drop the altitude from ![]() to
to ![]() and let it intersect
and let it intersect ![]() at
at ![]() . Then, let
. Then, let ![]() and thus
and thus ![]() . We then have by the Pythagorean Theorem on
. We then have by the Pythagorean Theorem on ![]() and
and ![]() :
:
 Then,
Then, ![]() . This gives us then from right triangle
. This gives us then from right triangle ![]() that
that ![]() and thus the ratio of
and thus the ratio of ![]() to
to ![]() is
is ![]() . From this, we see then that
. From this, we see then that ![]() and
and ![]() The Pythagorean Theorem on
The Pythagorean Theorem on ![]() then gives that
then gives that ![\[QD = \sqrt{AD^2 - AQ^2} = \sqrt{\left(\frac{27\sqrt{2}}{2}\right)^2 - 18^2} = \sqrt{\frac{81}{2}} = \frac{9\sqrt{2}}{2}.\]](http://latex.artofproblemsolving.com/7/9/2/7920b6201b85779a708f655e5b855697a42545ba.png) Then, we have the height of trapezoid
Then, we have the height of trapezoid ![]() is
is ![]() , the top base is
, the top base is ![]() , and the bottom base is
, and the bottom base is ![]() . From the equation of a trapezoid,
. From the equation of a trapezoid, ![]() , so the answer is
, so the answer is ![]() .
.
~lvmath
Solution 5 (Cyclic Quadrilaterals, Similar Triangles, Pythagorean Theorem)
Let ![]() and
and ![]() be the feet of the altitudes from
be the feet of the altitudes from ![]() to
to ![]() and
and ![]() , respectively.
, respectively.
Claim: We have ![]() pairs of similar right triangles:
pairs of similar right triangles: ![]() and
and ![]() .
.
Proof: Note that ![]() is cyclic. We need one more angle, and we get this from this cyclic quadrilateral:
is cyclic. We need one more angle, and we get this from this cyclic quadrilateral:
![]() Let
Let ![]() . We obtain from the similarities
. We obtain from the similarities ![]() and
and ![]() .
.
By Ptolemy, ![]() , so
, so ![]() .
.
We obtain ![]() , so
, so ![]() .
.
Applying the Pythagorean theorem on ![]() , we get
, we get ![]() .
.
Thus, ![]() , and
, and ![]() , yielding
, yielding ![]() .
.
Solution 6 (Similar Triangles and Trigonometry)
Let ![]() . Draw diagonal
. Draw diagonal ![]() and let
and let ![]() be the foot of the perpendicular from
be the foot of the perpendicular from ![]() to
to ![]() ,
, ![]() be the foot of the perpendicular from
be the foot of the perpendicular from ![]() to line
to line ![]() , and
, and ![]() be the foot of the perpendicular from
be the foot of the perpendicular from ![]() to
to ![]() .
.
Note that ![]() , and we get that
, and we get that ![]() . Therefore,
. Therefore, ![]() . It then follows that
. It then follows that ![]() . Using similar triangles, we can then find that
. Using similar triangles, we can then find that ![]() . Using the Law of Cosines on
. Using the Law of Cosines on ![]() , We can find that the
, We can find that the ![]() . Since
. Since ![]() , and each is supplementary to
, and each is supplementary to ![]() , we know that the
, we know that the ![]() . It then follows that
. It then follows that ![]() . Then it can be found that the area
. Then it can be found that the area ![]() is
is ![]() . Multiplying this by
. Multiplying this by ![]() , the answer is
, the answer is ![]() .
.
~happykeeper
Solution 7 (Similar Triangles and Trigonometry)
Draw the distances in terms of ![]() , as shown in the diagram. By similar triangles,
, as shown in the diagram. By similar triangles, ![]() . As a result, let
. As a result, let ![]() , then
, then ![]() and
and ![]() . The triangle
. The triangle ![]() is
is ![]() which
which ![]() . By angle subtraction,
. By angle subtraction, ![]() . Therefore,
. Therefore, ![]() and
and ![]() . By trapezoid area formula, the area of
. By trapezoid area formula, the area of ![]() is equal to
is equal to ![]() which
which ![]() .
.
~math2718281828459
Solution 8 (Heron's Formula)
![[asy] size(250); pair A, B, C, D, E, F, G, H; A = (-45sqrt(2)/8,18); B = (45sqrt(2)/8,18); C = (81sqrt(2)/8,0); D = (-81sqrt(2)/8,0); E = foot(A,C,B); F = foot(A,C,D); G = foot(A,B,D); H = intersectionpoint(A--F,B--D); markscalefactor=0.1; draw(rightanglemark(A,E,B),red); draw(rightanglemark(A,F,C),red); draw(rightanglemark(A,G,D),red); filldraw(A--D--F--cycle,yellow,black+linewidth(1.5)); filldraw(A--B--E--cycle,yellow,black+linewidth(1.5)); dot("$A$",A,1.5*NW,linewidth(4)); dot("$B$",B,1.5*NE,linewidth(4)); dot("$C$",C,1.5*SE,linewidth(4)); dot("$D$",D,1.5*SW,linewidth(4)); dot(E,linewidth(4)); dot(F,linewidth(4)); dot(G,linewidth(4)); label("$E$",E,NE); label("$F$",F, S); label("$G$",G,SE); draw(A--B--C--D--cycle^^B--D^^B--E); draw(A--E^^A--F^^A--G,dashed); label("$10$",midpoint(A--G),1.5*(1,0)); label("$15$",midpoint(A--E),1.5*N); label("$5x$",midpoint(A--B),S); label("$6x$",midpoint(A--D),1.5*(-1,0)); Label L = Label("$18$", align=(0,0), position=MidPoint, filltype=Fill(0,3,white)); draw(C+(5,0)--(81sqrt(2)/8,18)+(5,0), L=L, arrow=Arrows(),bar=Bars(15)); [/asy]](http://latex.artofproblemsolving.com/5/b/a/5ba5a49bb927904079fdebd1d30b6ff0abc4db74.png) Let the points formed by dropping altitudes from
Let the points formed by dropping altitudes from ![]() to the lines
to the lines ![]() ,
, ![]() , and
, and ![]() be
be ![]() ,
, ![]() , and
, and ![]() , respectively.
, respectively.
We have
![]() and
and
![]() For convenience, let
For convenience, let ![]() . By Heron's formula on
. By Heron's formula on ![]() , we have sides
, we have sides ![]() and semiperimeter
and semiperimeter ![]() , so
, so
![]() so
so ![]() .
.
Then,
![\[BE = \sqrt{AB^2 - CA^2} = \sqrt{\left(\frac{45}{2\sqrt{2}}\right)^2 - 15^2} = \sqrt{\frac{225}{8}} = \frac{15}{2\sqrt{2}}\]](http://latex.artofproblemsolving.com/c/a/d/cad3b2c06284cebae23b2afd7c928224b5f486ac.png) and
and
![]() Finally, recalling that
Finally, recalling that ![]() is isosceles,
is isosceles,
![]() so
so ![]() .
.
Solution 9 (Three Heights)
Let ![]() and
and ![]() be the perpendiculars from
be the perpendiculars from ![]() to
to ![]() and
and ![]() respectively.
respectively.
![]() .
Denote by
.
Denote by ![]() the base of the perpendicular from
the base of the perpendicular from ![]() to
to ![]() be the base of the perpendicular from
be the base of the perpendicular from ![]() to
to ![]() . Denote
. Denote ![]() It is clear that
It is clear that ![]() the area of
the area of ![]() is equal to the area of the rectangle
is equal to the area of the rectangle ![]()
The problem is reduced to finding ![]() .
.
In triangle ![]() all altitudes are known:
all altitudes are known:
![]()
![]() We apply the Law of Cosines to
We apply the Law of Cosines to ![]() and get
and get![]()
![]()
![]()
![]() We apply the Pythagorean Law to
We apply the Pythagorean Law to ![]() and get
and get![]()
![]()
![]() Required area is
Required area is
![]()
vladimir.shelomovskii@gmail.com, vvsss
Solution 10 (Area)
Let ![]() be on
be on ![]() such that
such that ![]() . Let
. Let ![]() be on
be on ![]() such that
such that ![]() .
.
Let ![]() be the length of
be the length of ![]() . Let
. Let ![]() be the length of
be the length of ![]() .
.
The area of ![]() can be expressed in three ways:
can be expressed in three ways: ![]() ,
, ![]() , and
, and ![]() .
.
![]()
![]()
![]()
![]()
Now, ![]() . We can substitute in
. We can substitute in ![]() to get
to get
![]() .
.
We have
![\[\frac{1}{2}(10)\left(\sqrt{m^2-100} + \sqrt{(\frac{6}{5}m)^2-100}\right) = \frac{1}{2}(18)(m)\]](http://latex.artofproblemsolving.com/3/d/e/3deae79105e168a3cfe2c255f4172bc7e85c869d.png) After a fairly straightforward algebraic bash, we get
After a fairly straightforward algebraic bash, we get ![]() , and
, and ![]() . By the Pythagorean Theorem on
. By the Pythagorean Theorem on ![]() ,
, ![]() , and
, and ![]() .
.
Thus, ![]() . Therefore,
. Therefore, ![]() . The requested answer is
. The requested answer is ![]() .
.
~ adam_zheng
Video Solution
~Mathproblemsolvingskills.com
Video Solution
https://www.youtube.com/watch?v=6rLnl8z7lnM
See Also
| 2021 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 8 |
Followed by Problem 10 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.