2021 April MIMC 10 Problems/Problem 22
Revision as of 17:51, 22 April 2021 by Cellsecret (talk | contribs) (Created page with "In the diagram, <math>ABCD</math> is a square with area <math>6+4\sqrt{2}</math>. <math>AC</math> is a diagonal of square <math>ABCD</math>. Square <math>IGED</math> has area...")
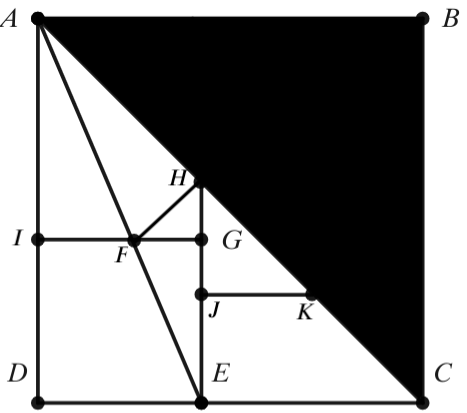
In the diagram, ![]() is a square with area
is a square with area ![]() .
. ![]() is a diagonal of square
is a diagonal of square ![]() . Square
. Square ![]() has area
has area ![]() . Given that point
. Given that point ![]() bisects line segment
bisects line segment ![]() , and
, and ![]() is a line segment. Extend
is a line segment. Extend ![]() to meet diagonal
to meet diagonal ![]() and mark the intersection point
and mark the intersection point ![]() . In addition,
. In addition, ![]() is drawn so that
is drawn so that ![]() .
. ![]() can be represented as
can be represented as ![]() where
where ![]() are not necessarily distinct integers. Given that
are not necessarily distinct integers. Given that ![]() , and
, and ![]() does not have a perfect square factor. Find
does not have a perfect square factor. Find ![]() .
.
![]()
Solution
To be Released on April 26th.