Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 IMO Problems/Problem 3"

(→‎Solution)
(→‎Solution)
Line 21: Line 21:
 
<math>\hspace{13mm}E</math> is the point of the circle <math>\Omega_1.</math>
 
<math>\hspace{13mm}E</math> is the point of the circle <math>\Omega_1.</math>
  
−
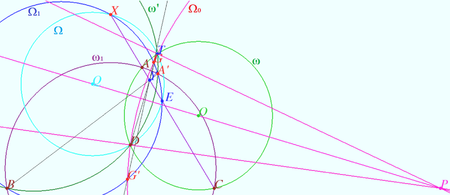
Let Y be the radical center of the circles <math>\omega, \omega',</math> and <math>\omega_1.</math> Let <math>T</math> be the point of intersection <math>\omega \cap \omega',</math> let <math>T'</math> be the point of intersection <math>\omega \cap \Omega.</math> Since the circles <math>\omega</math> and <math>\omega'</math> are inverse with respect to <math>\Omega_0,</math> then <math>T</math> lies on <math>\Omega_0,</math> and <math>P</math> lies on the perpendicular bisector of <math>DT.</math> The power of a point <math>Y</math> with respect to the circles  <math>\omega, \omega',</math> and <math>\Omega</math> are the same <math>(\boldsymbol{Lemma\hspace{3mm}2}),</math> so <math>DY\cdot YT = DY \cdot YT' \implies</math> the points <math>T</math> and <math>T'</math> coincide.
+
Let the point <math>Y</math> be the radical center of the circles <math>\omega, \omega', \omega_1.</math> It has the same power <math>\nu</math> with respect to these circles. The common chords of the pairs of circles <math>A'B, AC, DT</math> intersect at this point.
 +
<math>Y</math> has power <math>\nu</math> with respect to <math>\Omega_1</math> since <math>A'B</math> is the radical axis of <math>\omega', \omega_1, \Omega_1.</math>
 +
<math>Y</math> has power <math>\nu</math> with respect to <math>\Omega</math> since <math>XE</math> containing <math>Y</math> is the radical axis of <math>\Omega</math> and <math>\Omega_1.</math>
 +
Hence <math>Y</math> has power <math>\nu</math> with respect to <math>\omega, \omega', \Omega.</math>
  
 
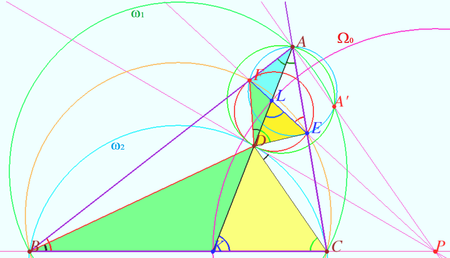
The centers of the circles  <math>\omega</math> and  <math>\Omega</math> (<math>O_1</math> and <math>O_2</math>) are located on the perpendicular bisector <math>DT'</math>, the point <math>P</math> is located on the perpendicular bisector <math>DT</math> and, therefore, the points <math>P, O_1,</math> and <math>O_2</math> lie on a line, that is, the lines <math>BC, EF,</math> and <math>O_1 O_2</math> are concurrent.
 
The centers of the circles  <math>\omega</math> and  <math>\Omega</math> (<math>O_1</math> and <math>O_2</math>) are located on the perpendicular bisector <math>DT'</math>, the point <math>P</math> is located on the perpendicular bisector <math>DT</math> and, therefore, the points <math>P, O_1,</math> and <math>O_2</math> lie on a line, that is, the lines <math>BC, EF,</math> and <math>O_1 O_2</math> are concurrent.
Line 36: Line 39:
 
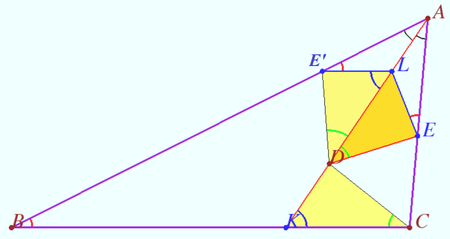
<cmath>\triangle ALE' \sim \triangle AKB \implies \frac {E'L}{BK}=  \frac {AL}{AK}\implies</cmath>
 
<cmath>\triangle ALE' \sim \triangle AKB \implies \frac {E'L}{BK}=  \frac {AL}{AK}\implies</cmath>
 
<cmath> \frac {AL}{DL} = \frac {AK \cdot DK}{BK \cdot KC}.</cmath>
 
<cmath> \frac {AL}{DL} = \frac {AK \cdot DK}{BK \cdot KC}.</cmath>
−
<i><b>Corollary</b></i>
+
Similarly, we prove that <math>FL</math> and <math>BC</math> are antiparallel with respect to angle <math>A,</math> and the points <math>L</math> in triangles <math>\triangle EDL</math> and <math>\triangle FDL</math> coincide. Hence, <math>FE</math> and <math>BC</math> are antiparallel and <math>BCEF</math> is cyclic.
 +
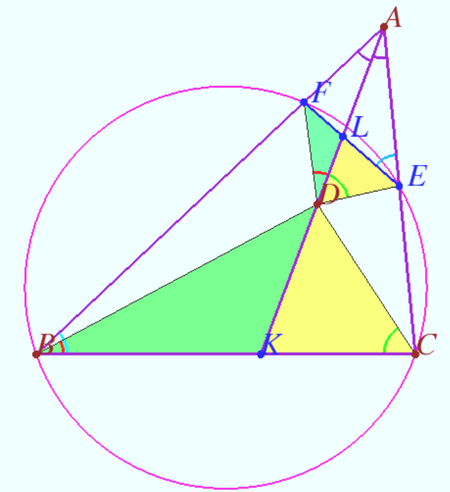
Note that the <math>\angle DFE =  \angle DLE –  \angle FDL =  \angle AKC –  \angle CBD</math> and
 +
<math>\angle PDE = 180^o –  \angle CDK –  \angle CDP –  \angle LDE</math>
 +
<math>\angle PDE = 180^o – (180^o –  \angle AKC –  \angle BCD) –  \angle CBD –  \angle BCD</math>
 +
<math>\angle PDE  =  \angle AKC –  \angle CBD = \angle DFE,</math>
  
−
In the given problem <math>EF</math> and <math>BC</math> are antiparallel with respect to the sides of an angle <math>A,</math> quadrangle <math>BCEF</math> is concyclic.
+
so <math>PD</math> is tangent to the circle <math>DEF.</math>
  
−
<math>\boldsymbol{Lemma \hspace{3mm}2}</math>
+
<math>PD^2 = PC \cdot PB = PE \cdot PF,</math> that is, the points <math>B</math> and <math>C, E</math> and <math>F</math> are inverse with respect to the circle <math>\Omega_0.</math>
  
−
Let the point <math>Y</math> be the radical center of the circles <math>\omega, \omega', \omega_1.</math> It has the same power <math>\nu</math> with respect to these circles.
 
−
The common chords of the pairs of circles <math>A'B, AC, DT</math> intersect at this point.
 
  
−
<math>Y</math> has the power <math>\nu</math> with respect to <math>\Omega_1</math> since <math>A'B</math> is the radical axis of <math>\omega', \omega_1, \Omega_1.</math>
 
−
 
−
<math>Y</math> has the power <math>\nu</math> with respect to <math>\Omega_1</math> since <math>XE</math> containing <math>Y</math> is the radical axis of <math>\Omega</math> and <math>\Omega_1.</math>
 
−
 
−
Hence <math>Y</math> has the same power <math>\nu</math> with respect to <math>\omega, \omega', \Omega.</math>
 
  
 
'''vladimir.shelomovskii@gmail.com, vvsss, www.deoma–cmd.ru'''
 
'''vladimir.shelomovskii@gmail.com, vvsss, www.deoma–cmd.ru'''

Revision as of 04:14, 23 July 2022

Problem

Let $D$ be an interior point of the acute triangle $ABC$ with $AB > AC$ so that $\angle DAB= \angle CAD$. The point $E$ on the segment $AC$ satisfies $\angle ADE= \angle BCD$, the point $F$ on the segment $AB$ satisfies $\angle FDA= \angle DBC$, and the point $X$ on the line $AC$ satisfies $CX=BX$. Let $O_1$ and $O_2$ be the circumcentres of the triangles $ADC$ and $EXD$ respectively. Prove that the lines $BC$, $EF$, and $O_1 O_2$ are concurrent.

Solution

2021 IMO 3f.png
2021 IMO 3e.png
2021 IMO 3.png
2021 IMO 3a.png

Let $P$ be the intersection point of the tangent to the circle $\omega_2 = BDC$ at the point $D$ and the line $BC, A'$ is inverse to $A$ with respect to the circle $\Omega_0$ centered at $P$ with radius $PD.$ Then the pairs of points $F$ and $E, B$ and $C$ are inverse with respect to $\Omega_0$, so the points $F, E,$ and $P$ are collinear. Quadrilaterals containing the pairs of inverse points $B$ and $C, E$ and $F, A$ and $A'$ are inscribed, $FE$ is antiparallel to $BC$ with respect to angle $A$ $(\boldsymbol{Lemma \hspace{3mm}1})$.

Consider the circles $\omega = ACD$ centered at $O_1, \omega' = A'BD,$ $\omega_1 = ABC, \Omega = EXD$ centered at $O_2 , \Omega_1 = A'BX,$ and $\Omega_0.$

Denote $\angle ACB = \gamma$. Then $\angle BXC = \angle BXE = \pi – 2\gamma,$ $\angle AA'B = \gamma (AA'CB$ is cyclic), $\angle AA'E = \pi – \angle AFE = \pi – \gamma (AA'EF$ is cyclic, $FE$ is antiparallel), $\angle BA'E = \angle AA'E – \angle AA'B = \pi – 2\gamma = \angle BXE \implies$

$\hspace{13mm}E$ is the point of the circle $\Omega_1.$

Let the point $Y$ be the radical center of the circles $\omega, \omega', \omega_1.$ It has the same power $\nu$ with respect to these circles. The common chords of the pairs of circles $A'B, AC, DT$ intersect at this point. $Y$ has power $\nu$ with respect to $\Omega_1$ since $A'B$ is the radical axis of $\omega', \omega_1, \Omega_1.$ $Y$ has power $\nu$ with respect to $\Omega$ since $XE$ containing $Y$ is the radical axis of $\Omega$ and $\Omega_1.$ Hence $Y$ has power $\nu$ with respect to $\omega, \omega', \Omega.$

The centers of the circles $\omega$ and $\Omega$ ($O_1$ and $O_2$) are located on the perpendicular bisector $DT'$, the point $P$ is located on the perpendicular bisector $DT$ and, therefore, the points $P, O_1,$ and $O_2$ lie on a line, that is, the lines $BC, EF,$ and $O_1 O_2$ are concurrent.

$\boldsymbol{Lemma \hspace{3mm}1}$

Let $AK$ be bisector of the triangle $ABC$, point $D$ lies on $AK.$ The point $E$ on the segment $AC$ satisfies $\angle ADE= \angle BCD$. The point $E'$ is symmetric to $E$ with respect to $AK.$ The point $L$ on the segment $AK$ satisfies $E'L||BC.$ Then $EL$ and $BC$ are antiparallel with respect to the sides of an angle $A$ and \[\frac {AL}{DL} = \frac {AK \cdot DK}{BK \cdot KC}.\] Proof

Symmetry of points $E$ and $E'$ with respect bisector $AK$ implies $\angle AEL = \angle AE'L.$ \[\angle DCK = \angle E'DL, \angle DKC = \angle E'LD \implies\] \[\triangle DCK \sim \triangle E'DL \implies \frac {E'L}{KD}= \frac {DL}{KC}.\] \[\triangle ALE' \sim \triangle AKB \implies \frac {E'L}{BK}= \frac {AL}{AK}\implies\] \[\frac {AL}{DL} = \frac {AK \cdot DK}{BK \cdot KC}.\] Similarly, we prove that $FL$ and $BC$ are antiparallel with respect to angle $A,$ and the points $L$ in triangles $\triangle EDL$ and $\triangle FDL$ coincide. Hence, $FE$ and $BC$ are antiparallel and $BCEF$ is cyclic. Note that the $\angle DFE = \angle DLE – \angle FDL = \angle AKC – \angle CBD$ and $\angle PDE = 180^o – \angle CDK – \angle CDP – \angle LDE$ $\angle PDE = 180^o – (180^o – \angle AKC – \angle BCD) – \angle CBD – \angle BCD$ $\angle PDE = \angle AKC – \angle CBD = \angle DFE,$

so $PD$ is tangent to the circle $DEF.$

$PD^2 = PC \cdot PB = PE \cdot PF,$ that is, the points $B$ and $C, E$ and $F$ are inverse with respect to the circle $\Omega_0.$


vladimir.shelomovskii@gmail.com, vvsss, www.deoma–cmd.ru

Video solution

https://youtu.be/cI9p-Z4-Sc8 [Video contains solutions to all day 1 problems]

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_IMO_Problems/Problem_3&oldid=176194"