2021 JMPSC Accuracy Problems

This is a fifteen question free-response test. Each question has exactly one integer answer.
You have 60 minutes to complete the test.
You will receive 4 points for each correct answer, and 0 points for each problem left unanswered or incorrect.
Figures are not necessarily drawn to scale.
No aids are permitted other than scratch paper, graph paper, rulers, and erasers. No calculators, smartwatches, or computing devices are allowed. No problems on the test will require the use of a calculator.

Problem 1

Find the sum of all positive multiples of $3$ that are factors of $27.$

Problem 2

Three distinct even positive integers are chosen between $1$ and $100,$ inclusive. What is the largest possible average of these three integers?

Solution

Problem 3

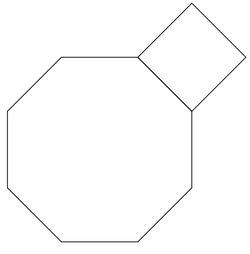
In a regular octagon, the sum of any three consecutive sides is $90.$ A square is constructed using one of the sides of this octagon. What is the area of the square?

Solution

Problem 4

If $\frac{x+2}{6}$ is its own reciprocal, find the product of all possible values of $x.$

Solution

Problem 5

Let $n!=n \cdot (n-1) \cdot (n-2) \cdots 2 \cdot 1$ for all positive integers $n$ . Find the value of $x$ that satisfies $\frac{5!x}{2022!}=\frac{20}{2021!}.$

Solution

Problem 6

In quadrilateral $ABCD$ , diagonal $\overline{AC}$ bisects both $\angle BAD$ and $\angle BCD$ . If $AB=15$ and $BC=13$ , find the perimeter of $ABCD$ .

Solution

Problem 7

If $A$ , $B$ , and $C$ each represent a single digit and they satisfy the equation $\begin{array}{cccc}& A & B & C \\ \times & & &3 \\ \hline & 7 & 9 & C\end{array},$ find $3A+2B+C$ .

Solution

Problem 8

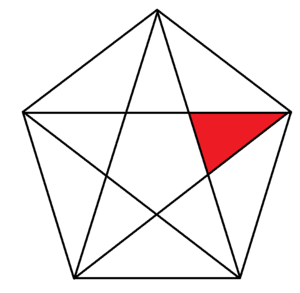
How many triangles are bounded by segments in the figure and contain the red triangle? (Do not include the red triangle in your total.)

Solution

Problem 9

If $x_1,x_2,\ldots,x_{10}$ is a strictly increasing sequence of positive integers that satisfies $\frac{1}{2}<\frac{2}{x_1}<\frac{3}{x_2}< \cdots < \frac{11}{x_{10}},$ find $x_1+x_2+\cdots+x_{10}$ .

Solution

Problem 10

In a certain school, each class has an equal number of students. If the number of classes was to increase by $1$ , then each class would have $20$ students. If the number of classes was to decrease by $1$ , then each class would have $30$ students. How many students are in each class?

Solution

Problem 11

If $a : b : c : d=1 : 2 : 3 : 4$ and $a$ , $b$ , $c$ , and $d$ are divisors of $252$ , what is the maximum value of $a$ ?

Solution

Problem 12

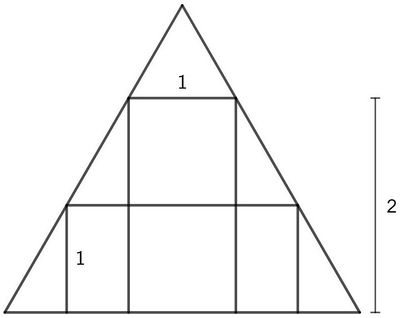
A rectangle with base $1$ and height $2$ is inscribed in an equilateral triangle. Another rectangle with height $1$ is also inscribed in the triangle. The base of the second rectangle can be written as a fully simplified fraction $\frac{a+b\sqrt{3}}{c}$ such that $gcd(a,b,c)=1.$ Find $a+b+c$ .

Solution

Problem 13

Let $x$ and $y$ be nonnegative integers such that $(x+y)^2+(xy)^2=25.$ Find the sum of all possible values of $x.$

Solution

Problem 14

What is the leftmost digit of the product $\underbrace{161616 \cdots 16}_{100 \text{ digits }} \times \underbrace{252525 \cdots 25}_{100 \text{ digits }}?$

Solution

Problem 15

For all positive integers $n,$ define the function $f(n)$ to output $4\underbrace{777 \cdots 7}_{n\ \text{sevens}}5.$ For example, $f(1)=475$ , $f(2)=4775$ , and $f(3)=47775.$ Find the last three digits of $\frac{f(1)+f(2)+ \cdots + f(100)}{25}.$