Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 USAMO Problems/Problem 1"
(→‎Solution: SEVERE LaTeX formatting fixing)
 
(5 intermediate revisions by 3 users not shown)
Line 1: Line 1:
−
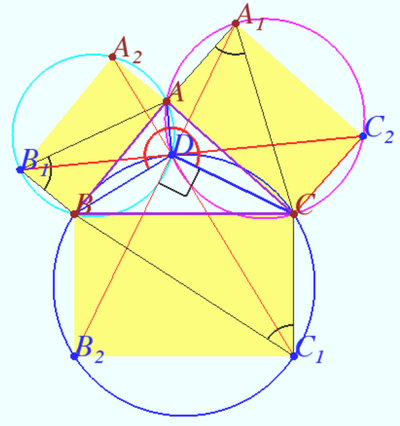
Prove that if a, b, and c are positive integers and n is an integer greater than 2, then the equality <math>a^n+b^n=c^n</math> cannot hold.
+
Rectangles <math>BCC_1B_2,</math> <math>CAA_1C_2,</math> and <math>ABB_1A_2</math> are erected outside an acute triangle <math>ABC.</math> Suppose that<cmath>\angle BC_1C+\angle CA_1A+\angle AB_1B=180^{\circ}.</cmath>Prove that lines <math>B_1C_2,</math> <math>C_1A_2,</math> and <math>A_1B_2</math> are concurrent.
 +
 
 +
==Solution==
 +
[[File:2021 USAMO 1.png|400px|right]]
 +
Let <math>D</math> be the second point of intersection of the circles <math>AB_1B</math> and <math>AA_1C.</math> Then:
 +
<cmath>\begin{align*}
 +
\angle ADB &= 180^\circ – \angle AB_1B,&\angle ADC &= 180^\circ – \angle AA_1C\\
 +
\angle BDC &= 360^\circ – \angle ADB – \angle ADC\\
 +
&= 360^\circ – (180^\circ – \angle AB_1B) – (180^\circ – \angle AA_1C)\\
 +
&= \angle AB_1B + \angle AA_1C\\
 +
\angle BDC + \angle BC_1C &= 180^\circ
 +
\end{align*}</cmath>
 +
Therefore, <math>BDCC_1B_2</math> is cyclic with diameters <math>BC_1</math> and <math>CB_2</math>, and thus <math>\angle CDB_2 = 90^\circ.</math>
 +
Similarly, <math>\angle CDA_1 = 90^\circ</math>, meaning points <math>A_1</math>, <math>D</math>, and <math>B_2</math> are collinear.
 +
 
 +
Similarly, the points <math>A_2, D, C_1</math> and <math>C_2, D, B_1</math> are collinear.
 +
 +
(After USAMO 2021 Solution Notes – Evan Chen)
 +
 
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 
 +
{{MAA Notice}}

Latest revision as of 13:32, 25 December 2023

Rectangles $BCC_1B_2,$ $CAA_1C_2,$ and $ABB_1A_2$ are erected outside an acute triangle $ABC.$ Suppose that\[\angle BC_1C+\angle CA_1A+\angle AB_1B=180^{\circ}.\]Prove that lines $B_1C_2,$ $C_1A_2,$ and $A_1B_2$ are concurrent.

Solution

2021 USAMO 1.png

Let $D$ be the second point of intersection of the circles $AB_1B$ and $AA_1C.$ Then: \begin{align*} \angle ADB &= 180^\circ – \angle AB_1B,&\angle ADC &= 180^\circ – \angle AA_1C\\ \angle BDC &= 360^\circ – \angle ADB – \angle ADC\\ &= 360^\circ – (180^\circ – \angle AB_1B) – (180^\circ – \angle AA_1C)\\ &= \angle AB_1B + \angle AA_1C\\ \angle BDC + \angle BC_1C &= 180^\circ \end{align*} Therefore, $BDCC_1B_2$ is cyclic with diameters $BC_1$ and $CB_2$, and thus $\angle CDB_2 = 90^\circ.$ Similarly, $\angle CDA_1 = 90^\circ$, meaning points $A_1$, $D$, and $B_2$ are collinear.

Similarly, the points $A_2, D, C_1$ and $C_2, D, B_1$ are collinear.

(After USAMO 2021 Solution Notes – Evan Chen)

vladimir.shelomovskii@gmail.com, vvsss

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_USAMO_Problems/Problem_1&oldid=208379"