2022 AMC 10A Problems/Problem 23
- The following problem is from both the 2022 AMC 10A #23 and 2022 AMC 12A #20, so both problems redirect to this page.
Contents
- 1 Problem
- 2 Solution 1 (Reflections + Ptolemy's Theorem)
- 3 Solution 2 (Extensions + Stewart's Theorem)
- 4 Solution 3 (Coordinate Bashing)
- 5 Solution 4 (Coordinate Bashing)
- 6 Solution 5 (Cheese)
- 7 Solution 6 (Pythagorean Theorem)
- 8 Video Solution by OmegaLearn
- 9 Video Solution By ThePuzzlr
- 10 Video Solution by Punxsutawney Phil
- 11 Video Solution by Steven Chen
- 12 Video Solution by MRENTHUSIASM (English & Chinese)
- 13 See also
Problem
Isosceles trapezoid ![]() has parallel sides
has parallel sides ![]() and
and ![]() with
with ![]() and
and ![]() There is a point
There is a point ![]() in the plane such that
in the plane such that ![]() and
and ![]() What is
What is ![]()
![]()
Solution 1 (Reflections + Ptolemy's Theorem)
Consider the reflection ![]() of
of ![]() over the perpendicular bisector of
over the perpendicular bisector of ![]() , creating two new isosceles trapezoids
, creating two new isosceles trapezoids ![]() and
and ![]() . Under this reflection,
. Under this reflection, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
Since ![]() and
and ![]() are isosceles trapezoids, they are cyclic. Using Ptolemy's theorem on
are isosceles trapezoids, they are cyclic. Using Ptolemy's theorem on ![]() , we get that
, we get that ![]() , so
, so
![]() Then, using Ptolemy's theorem again on
Then, using Ptolemy's theorem again on ![]() , we get that
, we get that ![]() , so
, so
![]() Thus,
Thus, ![]() and
and ![]() ; dividing these two equations and taking the reciprocal yields
; dividing these two equations and taking the reciprocal yields ![]() .
.
Solution 2 (Extensions + Stewart's Theorem)
![[asy] size(7.5cm); draw((0,0)--(4.2,0)); draw((0,0)--(1.4,2)--(2.8,2)--(4.2,0)); draw((1.4,2)--(2.1,3)--(2.8,2)); draw((0,0)--(1,0.5)--(1.4,2)--(1,0.5)--(2.8,2)--(1,0.5)--(4.2,0)); label("$A$",(0,0),SW); label("$B$",(1.4,2),NW); label("$C$",(2.8,2),NE); label("$D$",(4.2,0),SE); label("$P$",(1,0.5),NW); label("$Q$",(2.1,3),N); draw((2.1,3)--(1,0.5)); [/asy]](http://latex.artofproblemsolving.com/3/b/d/3bd9c6141356e4d6619922904795cf376feb15ae.png)
Extend ![]() and
and ![]() to a point
to a point ![]() as shown, and let
as shown, and let ![]() . Then let
. Then let ![]() and
and ![]() . Notice that
. Notice that ![]() by similar triangles.
by similar triangles.
By Stewart's theorem on ![]() and
and ![]() , we have
, we have ![]()
Subtracting, ![]() , and so
, and so ![]() .
.
~kred9 (minor edit by gwang2008)
Solution 3 (Coordinate Bashing)
Since we're given distances and nothing else, we can represent each point as a coordinate and use the distance formula to set up a series of systems and equations.
Let the height of the trapezoid be ![]() , and let the coordinates of
, and let the coordinates of ![]() and
and ![]() be at
be at ![]() and
and ![]() , respectively. Then let
, respectively. Then let ![]() and
and ![]() be at
be at ![]() and
and ![]() , respectively. This follows the rules that this is an isosceles trapezoid since the origin is centered on the middle of
, respectively. This follows the rules that this is an isosceles trapezoid since the origin is centered on the middle of ![]() . Finally, let
. Finally, let ![]() be located at point
be located at point ![]() .
.
The distance from ![]() to
to ![]() is
is ![]() , so by the distance formula:
, so by the distance formula: ![]() The distance from
The distance from ![]() to
to ![]() is
is ![]() , so
, so ![]()
Looking at these two equations alone, notice that the second term is the same for both equations, so we can subtract the equations. This yields ![]()
Next, the distance from ![]() to
to ![]() is
is ![]() , so
, so ![]() The distance from
The distance from ![]() to
to ![]() is
is ![]() , so
, so ![]()
Again, we can subtract these equations, yielding ![]()
We can now divide the equations to eliminate ![]() , yielding
, yielding ![]()
We wanted to find ![]() . But since
. But since ![]() is half of
is half of ![]() and
and ![]() is half of
is half of ![]() , this ratio is equal to the ratio we want.
, this ratio is equal to the ratio we want.
Therefore ![]() .
.
~KingRavi
Solution 4 (Coordinate Bashing)
Let the point ![]() be at the origin, and draw four concentric circles around
be at the origin, and draw four concentric circles around ![]() each with radius
each with radius ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , respectively. The vertices of the trapezoid would be then on each of the four concentric circles. WLOG, let
, respectively. The vertices of the trapezoid would be then on each of the four concentric circles. WLOG, let ![]() and
and ![]() be parallel to the x-axis. Assigning coordinates to each point, we have:
be parallel to the x-axis. Assigning coordinates to each point, we have: ![]()
![]()
![]()
![]() which satisfy the following:
which satisfy the following:
![]()
![]()
![]()
![]() In addition, because the trapezoid is isosceles (
In addition, because the trapezoid is isosceles (![]() ), the midpoints of the two bases would then have the same x-coordinate, giving us
), the midpoints of the two bases would then have the same x-coordinate, giving us
![]() Subtracting Equation
Subtracting Equation ![]() from Equation
from Equation ![]() , and Equation
, and Equation ![]() from Equation
from Equation ![]() , we have
, we have
![]()
![]() Dividing Equation
Dividing Equation ![]() by Equation
by Equation ![]() , we have
, we have
![]()
![]() Cancelling
Cancelling ![]() and
and ![]() with Equation
with Equation ![]() , we get
, we get
![]() In other words,
In other words,
![]() ~G63566
~G63566
Solution 5 (Cheese)
Notice that the question never says what the height of the trapezoid is; the only property we know about it is that ![]() . Therefore, we can say WLOG that the height of the trapezoid is
. Therefore, we can say WLOG that the height of the trapezoid is ![]() and all
and all ![]() points, including
points, including ![]() , lie on the same line with
, lie on the same line with ![]() . Notice that this satisfies the problem requirements because
. Notice that this satisfies the problem requirements because ![]() , and
, and ![]() .
Now all we have to find is
.
Now all we have to find is ![]() .
.
~KingRavi
Solution 6 (Pythagorean Theorem)
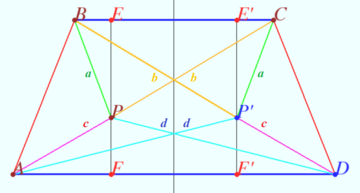
Consider the reflection ![]() of
of ![]() over the perpendicular bisector of
over the perpendicular bisector of ![]() .
.
![]() Let
Let ![]()
![]()
![]()
![]() Similarly,
Similarly,
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Video Solution by OmegaLearn
~ pi_is_3.14
Video Solution By ThePuzzlr
~ MathIsChess
Video Solution by Punxsutawney Phil
https://youtube.com/watch?v=uYXtEzX4fb0
Video Solution by Steven Chen
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Video Solution by MRENTHUSIASM (English & Chinese)
~MRENTHUSIASM
See also
| 2022 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 22 |
Followed by Problem 24 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
| 2022 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 19 |
Followed by Problem 21 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.