Difference between revisions of "2022 AMC 8 Problems/Problem 25"

Revision as of 14:42, 29 January 2022

Problem

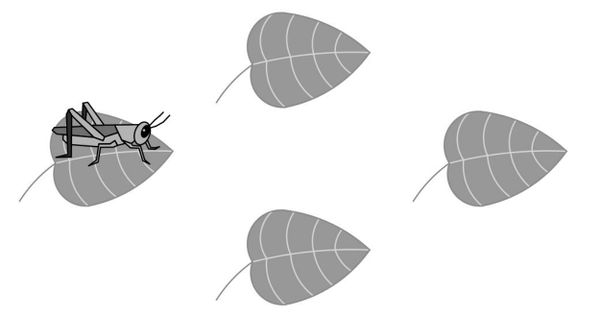
A cricket randomly hops between $4$ leaves, on each turn hopping to one of the other $3$ leaves with equal probability. After $4$ hops what is the probability that the cricket has returned to the leaf where it started?

$\textbf{(A) }\frac{2}{9}\qquad\textbf{(B) }\frac{19}{80}\qquad\textbf{(C) }\frac{20}{81}\qquad\textbf{(D) }\frac{1}{4}\qquad\textbf{(E) }\frac{7}{27}$

Solution 1 (Casework)

Let $A$ denote the leaf where the cricket starts and $B$ denote one of the other $3$ leaves. Note that:

If the cricket is at $A,$ then the probability that it hops to $B$ next is $1.$

If the cricket is at $B,$ then the probability that it hops to $A$ next is $\frac13.$

If the cricket is at $B,$ then the probability that it hops to $B$ next is $\frac23.$

We apply casework to the possible paths of the cricket:

$A \longrightarrow B \longrightarrow A \longrightarrow B \longrightarrow A$
The probability for this case is $1\cdot\frac13\cdot1\cdot\frac13=\frac19.$

$A \longrightarrow B \longrightarrow B \longrightarrow B \longrightarrow A$
The probability for this case is $1\cdot\frac23\cdot\frac23\cdot\frac13=\frac{4}{27}.$

Together, the probability that the cricket returns to $A$ is $\frac19+\frac{4}{27}=\boxed{\textbf{(E) }\frac{7}{27}}.$

~MRENTHUSIASM

Solution 2 (Recursion)

Denote $P_n$ to be the probability that the cricket would return back to the first point after $n$ hops. Then, we get the recursive formula $P_n = \frac13(1-P_{n-1})$ because if the leaf is not on the target leaf, then there is a $\frac13$ probability that it will make it back.

With this formula and the fact that $P_0=0,$ we have $P_1 = \frac13, P_2 = \frac29, P_3 = \frac7{27},$ so our answer is $\boxed{\textbf{(E) }\frac{7}{27}}$ .

~wamofan

Solution 3 (Also Casework)

We can label the leaves as shown:

[img]https://services.artofproblemsolving.com/download.php?id=YXR0YWNobWVudHMvZC85LzY0ZTU2ODBmZmRmZTgzMTdlM2VhMjQ3YTcxZDkwMDM5MmUxYmY2LnBuZw==&rn=MjAyMl9BTUM4XzI1X1NvbC5wbmc=[/img]

@@ Line 35: / Line 35: @@
 ~wamofan
+==Solution 3 (Also Casework)==
+We can label the leaves as shown:
+[img]https://services.artofproblemsolving.com/download.php?id=YXR0YWNobWVudHMvZC85LzY0ZTU2ODBmZmRmZTgzMTdlM2VhMjQ3YTcxZDkwMDM5MmUxYmY2LnBuZw==&rn=MjAyMl9BTUM4XzI1X1NvbC5wbmc=[/img]
 ==See Also==
 {{AMC8 box|year=2022|num-b=24|after=Last Problem}}
 {{MAA Notice}}

2022 AMC 8 (Problems • Answer Key • Resources)
Preceded by Problem 24	Followed by Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AJHSME/AMC 8 Problems and Solutions

Page

Toolbox

Search