Angle bisector
| This is an AoPSWiki Word of the Week for June 6-12 |
For an angle ![]() , the (internal) angle bisector of
, the (internal) angle bisector of ![]() is the line from B such that the angle between this line and
is the line from B such that the angle between this line and ![]() is congruent to the angle between this line and
is congruent to the angle between this line and ![]() :
:
A given angle ![]() also has an external angle bisector, which bisects external angle
also has an external angle bisector, which bisects external angle ![]() :
:
![[asy] pair A,B,C,D; B=(0,0); C=(5,0); A=(4,2); D=(3,4); draw(A--B--C--cycle,blue); draw(C--D,blue); dot(A^^B^^C,red); label("$A$",A,NE); label("$B$",B,W); label("$C$",C,E); [/asy]](http://latex.artofproblemsolving.com/b/4/f/b4fa3c523108f25c49d19f5e131710ab3e9864b1.png)
The two angle bisectors are perpendicular to each other and ![]()
Features of Angle Bisectors
- The distances from a point on an angle bisector to both of its sides are equal.
- The angle bisectors are the locus of points which are equidistant from the two sides of the angle.
- A reflection about either angle bisector maps the two sides of the angle to each other.
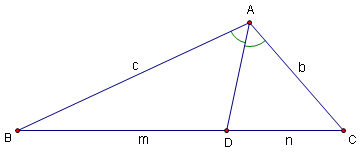
- In a triangle, the Angle Bisector Theorem gives the ratio in which the angle bisector cuts the opposite side.
- In a triangle, the internal angle bisectors (which are cevians) all intersect at the incenter of the triangle. The internal angle bisector of one angle and the external angle bisectors of the other two angles all intersect at an excenter of the triangle.
- A bisector of an angle can be constructed using a compass and straightedge.
|
|
| Triangle |
[[Image:Incenter.PNG|left|thumb|300px|Triangle ABC with incenter I, with angle bisectors (red), [[external angle bisectorincircle (blue), and inradii (green)]]
See also
This article is a stub. Help us out by expanding it.





![[asy] defaultpen(fontsize(8)); pair excenter(pair A, pair B, pair C){ pair X, Z; X=A+expi((angle(A-B)+angle(C-A))/2); Z=C+expi((angle(C-B)+angle(A-C))/2); return extension(X,A,Z,C); } pair X=(0,0), Y=(10,0), Z=(3,6); pair exX=excenter(Z,X,Y), exY=excenter(X,Y,Z), exZ=excenter(Y,Z,X); draw(circle(exX,length(exX-foot(exX,Y,Z)))); draw(circle(exY,length(exY-foot(exY,Z,X)))); draw(circle(exZ,length(exZ-foot(exZ,X,Y)))); draw((X-Y)+X--Y+1.5*(Y-X));draw((Y-Z)+Y--Z+(Z-Y));draw(2*(X-Z)+X--Z+2*(Z-X)); label("X",X,(-1.5,-1));label("Y",Y,(2,-1));label("Z",Z,N); label("P",exX,NE); dot(X^^Y^^Z^^exX^^exY^^exZ); draw(exX--(xpart(exX),0),dashed); real slope1=(ypart(Z)-ypart(X))/(xpart(Z)-xpart(X)); pair point1=exX+(1,-1/slope1); pair tangent1=extension(X,Z,point1,exX); draw(exX--tangent1,dashed); real slope2=(ypart(Y)-ypart(Z))/(xpart(Y)-xpart(Z)); pair point2=exX+(1,-1/slope2); pair tangent2=extension(Y,Z,point2,exX); draw(exX--tangent2,dashed); markscalefactor=0.1; draw(rightanglemark(exX,tangent1,Z)); draw(rightanglemark(exX,tangent2,Y)); draw(rightanglemark(exX,(xpart(exX),0),(100,0))); [/asy]](http://latex.artofproblemsolving.com/2/4/e/24ec521bb45c8a0d5a4eec1c2698079a9c8f192b.png)




