Difference between revisions of "Bibhorr Formula"
(→Units) |
|||
| (11 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | Bibhorr formula yields a [[equation|relation]] between three sides and [[angle]] of a [[right triangle]]. The [[angle]] which is equated to linear [[variable|variables]] is the Bibhorr [[angle]]. | ||
| + | The [[equation|formula]] is a superior alternative to [[trigonometry]] as it is devoid of [[sine]] and [[cosine]] functions. The [[equation]] establishes a [[geometry|geometric]] construction among the elements of a [[triangle]] as opposed to [[trigonometry]]. | ||
| + | |||
==Statement== | ==Statement== | ||
| − | For a given [[right triangle]] with longest side श्र, medium side लं and shortest side छ, the angle opposite the medium side (Bibhorr angle) बि is given as: | + | For a given [[right triangle]] with longest side श्र, medium side लं and shortest side छ, the [[angle]] opposite the medium side (Bibhorr angle) बि is given as: |
[[File:download.png|250px]] | [[File:download.png|250px]] | ||
| − | This [[equation]] is known as Bibhorr formula. The symbolical notations use Hindi letters and specifically denote the sides. | + | This [[equation]] is known as Bibhorr formula. The symbolical [[notation|notations]] use Hindi letters and specifically denote the sides. |
| − | + | ||
| + | ==Constants== | ||
| + | The use of two [[constant|constants]] - <math>90^{\circ}</math> or <math>\frac{\pi}{2}</math> and <math>1.5</math> makes the [[equation|formula]] more legible. These [[constant|constants]] are known as "Bibhorr sthiron" and "Bibhorr constant" respectively. | ||
| + | |||
==Units== | ==Units== | ||
| − | The | + | The units of Bibhorr [[angle]] depend on the the units of Bibhorr sthiron. If this [[constant|constants]] is <math>90^{\circ}</math> then [[angle]] is in [[Degree (geometry)|degrees]] but if Bibhorr sthiron is in the form <math>\frac{\pi}{2}</math> then Bibhorr [[angle]] results in [[radian|radians]]. |
==Explanation== | ==Explanation== | ||
[[File:Bibhorrformula.jpg]] | [[File:Bibhorrformula.jpg]] | ||
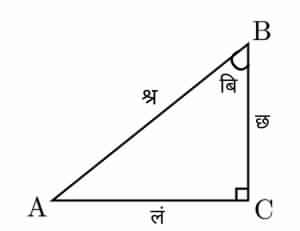
| − | Consider a [[right triangle]] ABC, such that BC and AC are shortest and medium sides respectively and AB is the longest side or hypotenuse. Now, the angle opposite AC, called Bibhorr angle is given as: | + | |
| + | Consider a [[right triangle]] ABC, such that BC and AC are shortest and medium sides respectively and AB is the longest side or [[hypotenuse]]. Now, the [[angle]] opposite AC, called Bibhorr [[angle]] is given as: | ||
| + | |||
[[File:download.png|250px]] | [[File:download.png|250px]] | ||
| + | |||
| + | ==See also== | ||
| + | *[[Trigonometry]] | ||
| + | *[[Geometry]] | ||
| + | *[[Right triangle]] | ||
Latest revision as of 06:45, 9 September 2018
Bibhorr formula yields a relation between three sides and angle of a right triangle. The angle which is equated to linear variables is the Bibhorr angle. The formula is a superior alternative to trigonometry as it is devoid of sine and cosine functions. The equation establishes a geometric construction among the elements of a triangle as opposed to trigonometry.
Contents
Statement
For a given right triangle with longest side श्र, medium side लं and shortest side छ, the angle opposite the medium side (Bibhorr angle) बि is given as:
This equation is known as Bibhorr formula. The symbolical notations use Hindi letters and specifically denote the sides.
Constants
The use of two constants - ![]() or
or ![]() and
and ![]() makes the formula more legible. These constants are known as "Bibhorr sthiron" and "Bibhorr constant" respectively.
makes the formula more legible. These constants are known as "Bibhorr sthiron" and "Bibhorr constant" respectively.
Units
The units of Bibhorr angle depend on the the units of Bibhorr sthiron. If this constants is ![]() then angle is in degrees but if Bibhorr sthiron is in the form
then angle is in degrees but if Bibhorr sthiron is in the form ![]() then Bibhorr angle results in radians.
then Bibhorr angle results in radians.
Explanation
Consider a right triangle ABC, such that BC and AC are shortest and medium sides respectively and AB is the longest side or hypotenuse. Now, the angle opposite AC, called Bibhorr angle is given as: