Difference between revisions of "Convex polygon"
(→See also) |
m |
||
| (6 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
[[Image:convex_polygon.png|right]] | [[Image:convex_polygon.png|right]] | ||
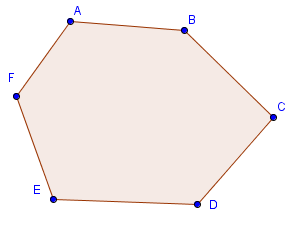
| − | A '''convex polygon''' is a [[polygon]] whose [[interior]] forms a [[convex set]]. That is, if any 2 points on the [[perimeter]] of the polygon are connected by a [[line segment]], no point on that segment will be outside the polygon. | + | A '''convex polygon''' is a [[polygon]] whose [[interior]] forms a [[convex set]]. That is, if any 2 points on the [[perimeter]] of the polygon are connected by a [[line segment]], no point on that segment will be outside the polygon. For example, every [[regular polygon]] is convex. |
| − | All [[ | + | All [[interior angle|interior angles]] of a convex polygon are less than <math>180^{\circ}</math>. Equivalently, all [[exterior angle|exterior angles]] are less than <math>180^{\circ}</math>. The sum of the exterior angles of any convex polygon is <math>360^\circ</math> and the sum of the internal angles of a convex <math>n</math>-gon is <math>(n - 2)180^\circ</math>. |
| − | The [[convex hull]] of a set of points | + | The [[convex hull]] of a [[finite]] set of points is a convex polygon with some or all of the points as its [[vertex | vertices]]. |
| − | |||
| − | |||
== See also == | == See also == | ||
* [[Concave polygon]] | * [[Concave polygon]] | ||
* [[Convex polyhedron]] | * [[Convex polyhedron]] | ||
| − | |||
{{stub}} | {{stub}} | ||
[[Category:Definition]] | [[Category:Definition]] | ||
| + | |||
| + | [[Category:Geometry]] | ||
Latest revision as of 22:10, 27 February 2020
A convex polygon is a polygon whose interior forms a convex set. That is, if any 2 points on the perimeter of the polygon are connected by a line segment, no point on that segment will be outside the polygon. For example, every regular polygon is convex.
All interior angles of a convex polygon are less than ![]() . Equivalently, all exterior angles are less than
. Equivalently, all exterior angles are less than ![]() . The sum of the exterior angles of any convex polygon is
. The sum of the exterior angles of any convex polygon is ![]() and the sum of the internal angles of a convex
and the sum of the internal angles of a convex ![]() -gon is
-gon is ![]() .
.
The convex hull of a finite set of points is a convex polygon with some or all of the points as its vertices.
See also
This article is a stub. Help us out by expanding it.