Difference between revisions of "Cyclic quadrilateral"
IntrepidMath (talk | contribs) |
(→Properties) |
||
| (24 intermediate revisions by 16 users not shown) | |||
| Line 1: | Line 1: | ||
| − | A | + | A '''cyclic quadrilateral''' is a [[quadrilateral]] that can be inscribed in a [[circle]]. While all [[triangles]] are cyclic, the same is not true of quadrilaterals. They have a number of interesting properties. |
| + | |||
| + | <center>[[image:Cyclicquad2.png]]</center> | ||
| + | |||
| + | == Properties == | ||
| + | |||
| + | In a quadrilateral <math>ABCD</math>: | ||
| + | |||
| + | * <math>\angle A + \angle C = \angle B + \angle D = {180}^{o} </math> This property is both sufficient and necessary (Sufficient & necessary = if and only if), and is often used to show that a quadrilateral is cyclic. | ||
| + | * <math>\angle ABD = \angle ACD</math> | ||
| + | * <math>\angle BCA = \angle BDA</math> | ||
| + | * <math>\angle BAC = \angle BDC</math> | ||
| + | * <math>\angle CAD = \angle CBD</math> | ||
| + | * All four [[perpendicular bisector|perpendicular bisectors]] are [[concurrent]]. The converse is also true. This intersection is the [[circumcenter]] of the quadrilateral. | ||
| + | * Any two opposite sites of the quadrilateral are antiparallel with respect to the other two opposite sites. | ||
| + | |||
| + | == Applicable Theorems/Formulae == | ||
| + | |||
| + | The following theorems and formulae apply to cyclic quadrilaterals: | ||
| + | |||
| + | * [[Ptolemy's Theorem]] | ||
| + | * [[Brahmagupta's formula]] | ||
| + | |||
| + | [[Category:Definition]] | ||
| + | |||
| + | [[Category:Geometry]] | ||
| + | |||
| + | {{stub}} | ||
Latest revision as of 20:39, 9 March 2024
A cyclic quadrilateral is a quadrilateral that can be inscribed in a circle. While all triangles are cyclic, the same is not true of quadrilaterals. They have a number of interesting properties.
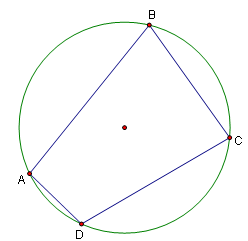
Properties
In a quadrilateral 
:
This property is both sufficient and necessary (Sufficient & necessary = if and only if), and is often used to show that a quadrilateral is cyclic.
- All four perpendicular bisectors are concurrent. The converse is also true. This intersection is the circumcenter of the quadrilateral.
- Any two opposite sites of the quadrilateral are antiparallel with respect to the other two opposite sites.
This property is both sufficient and necessary (Sufficient & necessary = if and only if), and is often used to show that a quadrilateral is cyclic.
Applicable Theorems/Formulae
The following theorems and formulae apply to cyclic quadrilaterals:
This article is a stub. Help us out by expanding it.
