Difference between revisions of "Mock AIME 2 2006-2007 Problems"
(→Problem 9) |
(→Problem 7) |
||
| Line 30: | Line 30: | ||
== Problem 7 == | == Problem 7 == | ||
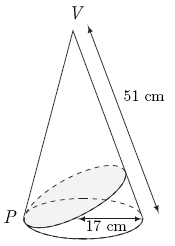
| − | A right circular cone of base radius <math>\displaystyle 17</math>cm and slant height <math>\displaystyle 34</math>cm is given. <math>\displaystyle P</math> is a point on the circumference of the base and the shortest path from <math>\displaystyle P</math> around the cone and back is drawn (see diagram). If the | + | A right circular cone of base radius <math>\displaystyle 17</math>cm and slant height <math>\displaystyle 34</math>cm is given. <math>\displaystyle P</math> is a point on the circumference of the base and the shortest path from <math>\displaystyle P</math> around the cone and back is drawn (see diagram). If the length of this path is <math>\displaystyle m\sqrt{n},</math> where <math>\displaystyle m</math> and <math>\displaystyle n</math> are relatively prime positive integers, find <math>\displaystyle m+n.</math> |
| − | [[Image: | + | [[Image:Mock_AIME_2_2007_Problem8.jpg]] |
[[Mock_AIME_2_2006-2007/Problem_7|Solution]] | [[Mock_AIME_2_2006-2007/Problem_7|Solution]] | ||
Revision as of 14:09, 25 July 2006
Contents
Problem 1
A positive integer is called a dragon if it can be partitioned into four positive integers ![]() and
and ![]() such that
such that ![]() Find the smallest dragon.
Find the smallest dragon.
Problem 2
The set ![]() consists of all integers from
consists of all integers from ![]() to
to ![]() inclusive. For how many elements
inclusive. For how many elements ![]() in
in ![]() is
is ![]() an integer?
an integer?
Problem 3
Let ![]() be the sum of all positive integers
be the sum of all positive integers ![]() such that
such that ![]() is a perfect square. Find the remainder when
is a perfect square. Find the remainder when ![]() is divided by
is divided by ![]()
Problem 4
Let ![]() be the smallest positive integer for which there exist positive real numbers
be the smallest positive integer for which there exist positive real numbers ![]() and
and ![]() such that
such that ![]() . Compute
. Compute ![]() .
.
Problem 5
Given that ![]() and
and ![]() find
find ![]()
Problem 6
If ![]() and
and ![]() find
find ![]()
Problem 7
A right circular cone of base radius ![]() cm and slant height
cm and slant height ![]() cm is given.
cm is given. ![]() is a point on the circumference of the base and the shortest path from
is a point on the circumference of the base and the shortest path from ![]() around the cone and back is drawn (see diagram). If the length of this path is
around the cone and back is drawn (see diagram). If the length of this path is ![]() where
where ![]() and
and ![]() are relatively prime positive integers, find
are relatively prime positive integers, find ![]()
Problem 8
The positive integers ![]() satisfy
satisfy ![]() and
and ![]() for
for ![]() . Find the last three digits of
. Find the last three digits of ![]() .
.
Problem 9
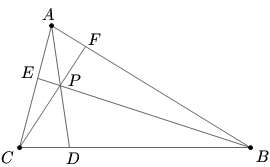
In right triangle ![]()
![]() Cevians
Cevians ![]() and
and ![]() intersect at
intersect at ![]() and are drawn to
and are drawn to ![]() and
and ![]() respectively such that
respectively such that ![]() and
and ![]() If
If ![]() where
where ![]() and
and ![]() are relatively prime and
are relatively prime and ![]() has no perfect square divisors excluding
has no perfect square divisors excluding ![]() find
find ![]()
Problem 10
Find the number of solutions, in degrees, to the equation ![]() where
where ![]()
Problem 11
Find the sum of the squares of the roots, real or complex, of the system of simultaneous equations
![]()
Problem 12
In quadrilateral ![]()
![]() and
and ![]() If
If ![]()
![]() ,
, ![]() and the area of
and the area of ![]() is
is ![]() where
where ![]() are relatively prime positive integers, find
are relatively prime positive integers, find ![]()
Note*: ![]() and
and ![]() refer to the areas of triangles
refer to the areas of triangles ![]() and
and ![]()
Problem 13
In his spare time, Richard Rusczyk shuffles a standard deck of 52 playing cards. He then turns the cards up one by one from the top of the deck until the third ace appears. If the expected (average) number of cards Richard will turn up is ![]() where
where ![]() and
and ![]() are relatively prime positive integers, find
are relatively prime positive integers, find ![]()
Problem 14
In triangle ABC, ![]() and
and ![]() Given that
Given that ![]() ,
, ![]() and
and ![]() intersect at
intersect at ![]() and are an angle bisector, median, and altitude of the triangle, respectively, compute the length of
and are an angle bisector, median, and altitude of the triangle, respectively, compute the length of ![]()
Problem 15
A ![]() cube is composed of
cube is composed of ![]() unit cubes. The faces of
unit cubes. The faces of ![]() unit cubes are colored red. An arrangement of the cubes is
unit cubes are colored red. An arrangement of the cubes is ![]() if there is exactly
if there is exactly ![]() red unit cube in every
red unit cube in every ![]() rectangular box composed of
rectangular box composed of ![]() unit cubes. Determine the number of
unit cubes. Determine the number of ![]() colorings.
colorings.