Difference between revisions of "Mock AIME 2 2006-2007 Problems/Problem 14"
(→Problem) |
|||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
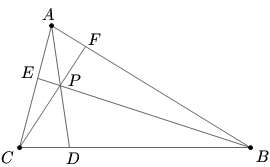
| − | In triangle ABC, <math>\displaystyle AB = 308</math> and <math>\displaystyle AC=35.</math> Given that <math>\displaystyle AD</math>, <math>\displaystyle BE,</math> and <math>\displaystyle CF,</math> intersect at <math>\displaystyle P</math> and are an angle bisector, median, and altitude of the triangle, respectively, compute the length of <math>\displaystyle BC.</math> | + | In triangle ABC, <math>\displaystyle AB = 308</math> and <math>\displaystyle AC=35.</math> Given that <math>\displaystyle AD</math>, <math>\displaystyle BE,</math> and <math>\displaystyle CF,</math> intersect at <math>\displaystyle P</math> and are an angle bisector, median, and altitude of the triangle, respectively, compute the length of <math>\displaystyle BC.</math> |
| + | |||
| + | [[Image:Mock AIME 2 2007 Problem14.jpg]] | ||
== Problem Source == | == Problem Source == | ||
4everwise thought of this problem after reading the first chapter of Geometry Revisited. | 4everwise thought of this problem after reading the first chapter of Geometry Revisited. | ||