Difference between revisions of "Mock AIME 2 2006-2007 Problems/Problem 7"
m (categorized) |
God of Math (talk | contribs) (→Solution) |
||
| Line 7: | Line 7: | ||
==Solution== | ==Solution== | ||
{{solution}} | {{solution}} | ||
| + | |||
| + | We begin by noticing that that the shortest path from a point on the base to and around the cone is the perpendicular from the aforementioned point to the slant line. We can now construct two equations based on this fact. Let x be the length from the point on the other end of the diameter from P to the point at which P is perpendicular to the slant. Let y now be the diameter of the shaded circle. We now have two equations : <math>x_{}^{2} + y_{}^{2} = 34_{}^{}</math> and <math>y_{}^{2} + (34 - x)_{}^{2} = 34_{}^{2}</math>. We can tell from this equation that <math>34 - x = x</math>, so <math>x = 17</math>. From this we can deduce that y = $17*sqrt(3) | ||
| + | |||
| + | |||
| + | |||
| + | |||
---- | ---- | ||
Revision as of 15:14, 25 April 2009
Problem
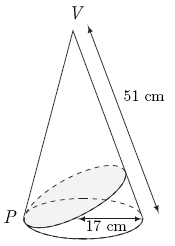
A right circular cone of base radius ![]() cm and slant height
cm and slant height ![]() cm is given.
cm is given. ![]() is a point on the circumference of the base and the shortest path from
is a point on the circumference of the base and the shortest path from ![]() around the cone and back is drawn (see diagram). If the length of this path is
around the cone and back is drawn (see diagram). If the length of this path is ![]() where
where ![]() and
and ![]() are relatively prime positive integers, find
are relatively prime positive integers, find ![]()
Solution
This problem needs a solution. If you have a solution for it, please help us out by adding it.
We begin by noticing that that the shortest path from a point on the base to and around the cone is the perpendicular from the aforementioned point to the slant line. We can now construct two equations based on this fact. Let x be the length from the point on the other end of the diameter from P to the point at which P is perpendicular to the slant. Let y now be the diameter of the shaded circle. We now have two equations : ![]() and
and ![]() . We can tell from this equation that
. We can tell from this equation that ![]() , so
, so ![]() . From this we can deduce that y = $17*sqrt(3)
. From this we can deduce that y = $17*sqrt(3)