Difference between revisions of "Orthic triangle"
Etmetalakret (talk | contribs) |
Etmetalakret (talk | contribs) |
||
| Line 35: | Line 35: | ||
== Problems == | == Problems == | ||
===Olympiad=== | ===Olympiad=== | ||
| − | * Let <math>\triangle ABC</math> be an acute triangle with <math>D</math>, <math>E</math>, <math>F</math> the feet of the altitudes lying on <math>\overline{BC}</math>, <math>\overline{CA}</math>, and <math>\overline{AB | + | * Let <math>\triangle ABC</math> be an acute triangle with <math>D</math>, <math>E</math>, <math>F</math> the feet of the altitudes lying on <math>\overline{BC}</math>, <math>\overline{CA}</math>, and <math>\overline{AB}</math> respectively. One of the intersection points of the line <math>\overline{EF}</math> and the circumcircle is <math>P</math>. The lines <math>\overline{BP}</math> and <math>\overline{DF}</math> meet at point <math>Q</math>. Prove that <math>|AP| = |AQ|</math>. (IMO Shortlist 2010 G1) |
== See also == | == See also == | ||
Revision as of 13:14, 10 May 2021
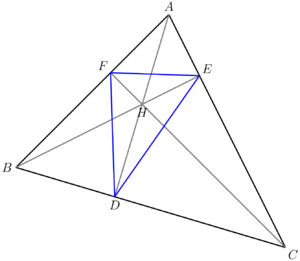
In geometry, given any ![]() , let
, let ![]() ,
, ![]() , and
, and ![]() denote the feet of the altitudes from
denote the feet of the altitudes from ![]() ,
, ![]() , and
, and ![]() , respectively. Then,
, respectively. Then, ![]() is called the orthic triangle of
is called the orthic triangle of ![]() .
.
It's easy to see that there is no orthic triangle if ![]() is right. The only two cases are when
is right. The only two cases are when ![]() is either acute or obtuse.
is either acute or obtuse.
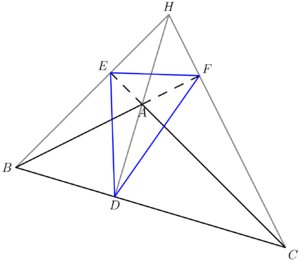
Orthic triangles are not unique to their mother triangles, as one acute and one to three obtuse triangles are guaranteed to have the same orthic triangle. To see this, take an acute triangle and swap its orthocenter and any vertex to get an obtuse triangle. It's easy to verify that this placement of the orthocenter is correct, and that the orthic triangle will remain the same as before.
Contents
Cyclic quadrilaterals
In both the acute and obtuse case, quadrilaterals ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are cyclic.
are cyclic.
Proof: we will be using directed angles, denoted by ![]() instead of the conventional
instead of the conventional ![]() . We know that
. We know that ![]() and thus
and thus ![]() is cyclic. In addition,
is cyclic. In addition, ![]() so
so ![]() is also cyclic. It follows that the other cyclic quadrilaterals are also cyclic.
is also cyclic. It follows that the other cyclic quadrilaterals are also cyclic. ![]()
These cyclic quadrilaterals make frequent appearances in olympiad geometry and are the most crucial section of this article.
Connection with incenters and excenters
Incenter of the orthic triangle
If ![]() is acute, then the incenter of the orthic triangle is the orthocenter
is acute, then the incenter of the orthic triangle is the orthocenter ![]() .
.
If ![]() is obtuse, then the incenter of the orthic triangle is the obtuse vertex.
is obtuse, then the incenter of the orthic triangle is the obtuse vertex.
Excenters of the orthic triangle
For any ![]() and
and ![]() ,
, ![]() is the orthic triangle of
is the orthic triangle of ![]() if and only if
if and only if ![]() ,
, ![]() , and
, and ![]() are the excenters of
are the excenters of ![]() .
.
Proof: (for excenters -> orthic triangle, note that AD perp BC. Thus, AD is an altitude of ![]() , with foot
, with foot ![]() . Similarly, the others go and we have
. Similarly, the others go and we have ![]() and
and ![]() are the feet of the altitudes, so
are the feet of the altitudes, so ![]() is the orthic trianlge) (for orthic triangle -> excenters, note that
is the orthic trianlge) (for orthic triangle -> excenters, note that ![]() and
and ![]() . then BC is the exterior bisector of FDE. similarly, AB and CA are exterior bisectors, so they intersect at the excenters, ie A, B, and C)
. then BC is the exterior bisector of FDE. similarly, AB and CA are exterior bisectors, so they intersect at the excenters, ie A, B, and C)
This lemma also applies in reverse. In the acute case, ![]() ,
, ![]() , and
, and ![]() are the excenters of the orthic triangle, while in the obtuse case, the two vertexes with acute angles and the orthocenter of
are the excenters of the orthic triangle, while in the obtuse case, the two vertexes with acute angles and the orthocenter of ![]() are the excenters.
are the excenters.
Relationship with the incenter/excenter lemma
With this knowledge in mind, we can transfer results about the incenter and excenters to the orthic triangle. In particular, the incenter/excenter lemma can be translated into the language of the orthic triangle. It tells that all six cyclic quadrilaterals of the orthic triangle have a circumcenter on the nine-point circle of ![]() .
.
In the case where ![]() is acute, quadrilaterals
is acute, quadrilaterals ![]() ,
, ![]() , and
, and ![]() follow immediately from the lemma. As for
follow immediately from the lemma. As for ![]() ,
, ![]() , and
, and ![]() , via the inscribed angle theorem, their circumcenters are the midpoints of the side lengths of
, via the inscribed angle theorem, their circumcenters are the midpoints of the side lengths of ![]() , which we know to be on the nine-point circle. Identical reasoning follows that the six cyclic quadrilaterals also have circumcenters on the nine-point circle.
, which we know to be on the nine-point circle. Identical reasoning follows that the six cyclic quadrilaterals also have circumcenters on the nine-point circle.
Problems
Olympiad
- Let
 be an acute triangle with
be an acute triangle with  ,
,  ,
,  the feet of the altitudes lying on
the feet of the altitudes lying on  ,
,  , and
, and  respectively. One of the intersection points of the line
respectively. One of the intersection points of the line  and the circumcircle is
and the circumcircle is  . The lines
. The lines  and
and  meet at point
meet at point  . Prove that
. Prove that  . (IMO Shortlist 2010 G1)
. (IMO Shortlist 2010 G1)