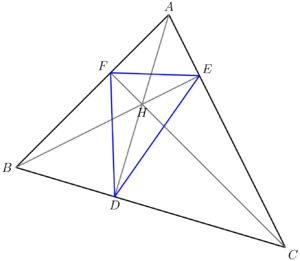
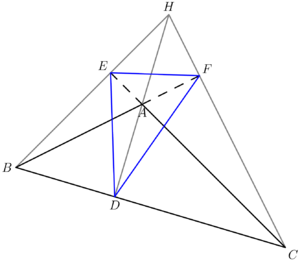
Orthic triangle
In geometry, given any ![]() , let
, let ![]() ,
, ![]() , and
, and ![]() denote the feet of the altitudes from
denote the feet of the altitudes from ![]() ,
, ![]() , and
, and ![]() , respectively. Then,
, respectively. Then, ![]() is called the orthic triangle of
is called the orthic triangle of ![]() .
.
It's easy to see that there is no orthic triangle if ![]() is right. The two cases are when
is right. The two cases are when ![]() is either acute or obtuse must be handled separately, as they each carry different characteristics.
is either acute or obtuse must be handled separately, as they each carry different characteristics.
Orthic triangles are not unique to their mother triangles, as one acute and one to three obtuse triangles are guaranteed to have the same orthic triangle. To see this, take an acute triangle and swap its orthocenter and any vertex to get an obtuse triangle. It's easy to verify that this placement of the orthocenter is correct and that the orthic triangle will remain the same as before the swapping, as seen in the diagrams to the right.
Contents
Cyclic quadrilaterals
In both the acute and obtuse case, quadrilaterals ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are cyclic.
are cyclic.
Proof: we will be using directed angles, denoted by ![]() instead of the conventional
instead of the conventional ![]() . We know that
. We know that ![]() and thus
and thus ![]() is cyclic. In addition,
is cyclic. In addition, ![]() so
so ![]() is also cyclic. It follows that the other cyclic quadrilaterals are also cyclic.
is also cyclic. It follows that the other cyclic quadrilaterals are also cyclic. ![]()
These cyclic quadrilaterals make frequent appearances in olympiad geometry and are the most crucial section of this article.
Connection with incenters and excenters
Incenter of the orthic triangle
If ![]() is acute, then the incenter of the orthic triangle of
is acute, then the incenter of the orthic triangle of ![]() is the orthocenter
is the orthocenter ![]() .
.
Proof:
If ![]() is obtuse, then the incenter of the orthic triangle of
is obtuse, then the incenter of the orthic triangle of ![]() is the obtuse vertex.
is the obtuse vertex.
Excenters of the orthic triangle
For any acute ![]() and any
and any ![]() ,
, ![]() is the orthic triangle of
is the orthic triangle of ![]() if and only if
if and only if ![]() ,
, ![]() , and
, and ![]() are the excenters of
are the excenters of ![]() .
.
Proof: First, we show that the orthic triangle leads to the excenters. Let ![]() ,
, ![]() , and
, and ![]() be on
be on ![]() ,
, ![]() , and
, and ![]() , respectively. Because
, respectively. Because ![]() is cyclic,
is cyclic, ![]() . Likewise,
. Likewise, ![]() as well. Then because
as well. Then because ![]() ,
, ![]() and so
and so ![]() .
.
Thus, the exterior angle of ![]() is
is ![]() . But
. But ![]() , so
, so ![]() bisects the exterior angle of
bisects the exterior angle of ![]() . Similarly,
. Similarly, ![]() and
and ![]() bisect the exterior angles of
bisect the exterior angles of ![]() and
and ![]() respectively. Thus, the intersections of
respectively. Thus, the intersections of ![]() ,
, ![]() , and
, and ![]() (namely
(namely ![]() ,
, ![]() , and
, and ![]() ) are the excenters of
) are the excenters of ![]() , and we're done.
, and we're done.
Next, we show that the excenters lead to the orthic triangle. Let ![]() ,
, ![]() , and
, and ![]() be the
be the ![]() -excenter,
-excenter, ![]() -excenter, and
-excenter, and ![]() -excenter of
-excenter of ![]() , and let
, and let ![]() be the incenter of
be the incenter of ![]() .
. ![]() is equidistant from
is equidistant from ![]() and
and ![]() , so
, so ![]() is on
is on ![]() , and
, and ![]() is an internal angle bisector of
is an internal angle bisector of ![]() .
.
We know that ![]() and because
and because ![]() is an
is an ![]() -excenter of
-excenter of ![]() ,
, ![]() . Thus,
. Thus, ![]() , and because
, and because ![]() is on
is on ![]() ,
, ![]() is the foot of the altitude from
is the foot of the altitude from ![]() of
of ![]() . Similarly,
. Similarly, ![]() and
and ![]() are feet of the altitudes from
are feet of the altitudes from ![]() and
and ![]() , respectively. Then
, respectively. Then ![]() is the orthic triangle of
is the orthic triangle of ![]() , and we are done.
, and we are done. ![]()
In the obtuse case, the two vertices with acute angles and the orthocenter of ![]() are the excenters.
are the excenters.
Relationship with the incenter/excenter lemma
With this knowledge in mind, we can transfer results about the incenter and excenters to the orthic triangle. In particular, the incenter/excenter lemma can be translated into the language of the orthic triangle. It tells that all six cyclic quadrilaterals of the orthic triangle have a circumcenter on the nine-point circle of ![]() .
.
In the case where ![]() is acute, quadrilaterals
is acute, quadrilaterals ![]() ,
, ![]() , and
, and ![]() follow immediately from the lemma. Actually, because
follow immediately from the lemma. Actually, because ![]() , the circumcenter of
, the circumcenter of ![]() is the midpoint of
is the midpoint of ![]() and
and ![]() , called an Euler point. It follows that the circumcenters of
, called an Euler point. It follows that the circumcenters of ![]() and
and ![]() are the other two Euler points.
are the other two Euler points.
As for ![]() ,
, ![]() , and
, and ![]() , via the inscribed angle theorem, their circumcenters are the midpoints of the side lengths of
, via the inscribed angle theorem, their circumcenters are the midpoints of the side lengths of ![]() , which we know to be on the nine-point circle.
, which we know to be on the nine-point circle.
Identical reasoning follows that in the obtuse case, the six cyclic quadrilaterals still have circumcenters on the nine-point circle.
Problems
Olympiad
- Let
 be an acute triangle with
be an acute triangle with  ,
,  ,
,  the feet of the altitudes lying on
the feet of the altitudes lying on  ,
,  , and
, and  respectively. One of the intersection points of the line
respectively. One of the intersection points of the line  and the circumcircle is
and the circumcircle is  . The lines
. The lines  and
and  meet at point
meet at point  . Prove that
. Prove that  . (IMO Shortlist 2010 G1)
. (IMO Shortlist 2010 G1)