Pythagorean Theorem
This article is a stub. Help us out by expanding it.
The Pythagorean Theorem states that for a right triangle with legs of length ![]() and
and ![]() and hypotenuse of length
and hypotenuse of length ![]() we have the relationship
we have the relationship ![]() . This theorem has been know since antiquity and is a classic to prove; hundreds of proofs have been published and many can be demonstrated entirely visually. The Pythagorean Theorem is one of the most frequently used theorems in geometry, and is one of the many tools in a good geometer's arsenal. A very large number of geometry problems can be solved by building right triangles and applying the Pythagorean Theorem.
. This theorem has been know since antiquity and is a classic to prove; hundreds of proofs have been published and many can be demonstrated entirely visually. The Pythagorean Theorem is one of the most frequently used theorems in geometry, and is one of the many tools in a good geometer's arsenal. A very large number of geometry problems can be solved by building right triangles and applying the Pythagorean Theorem.
This is generalized by the Pythagorean Inequality and the Law of Cosines.
Contents
Proofs
In these proofs, we will let ![]() be any right triangle with a right angle at
be any right triangle with a right angle at ![]() .
.
Proof 1
We use ![]() to denote the area of triangle
to denote the area of triangle ![]() .
.
Let ![]() be the perpendicular to side
be the perpendicular to side ![]() from
from ![]() .
.
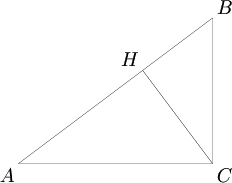
Since ![]() are similar right triangles, and the areas of similar triangles are proportionate to the squares of corresponding side lengths,
are similar right triangles, and the areas of similar triangles are proportionate to the squares of corresponding side lengths,
![]() .
.
But since triangle ![]() is composed of triangles
is composed of triangles ![]() and
and ![]() ,
, ![]() , so
, so ![]() . ∎
. ∎
Proof 2
Consider a circle ![]() with center
with center ![]() and radius
and radius ![]() . Since
. Since ![]() and
and ![]() are perpendicular,
are perpendicular, ![]() is tangent to
is tangent to ![]() . Let the line
. Let the line ![]() meet
meet ![]() at
at ![]() and
and ![]() , as shown in the diagram:
, as shown in the diagram:
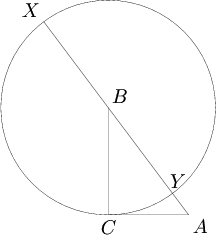
Evidently, ![]() and
and ![]() . By considering the power of point
. By considering the power of point ![]() with respect to
with respect to ![]() , we see
, we see
![]() . ∎
. ∎
Introductory
Example Problems
Common Pythagorean Triples
A Pythagorean Triple is a set of 3 positive integers such that ![]() , i.e. the 3 numbers can be the lengths of the sides of a right triangle. Among these, the Primitive Pythagorean Triples, those in which the three numbers have no common divisor, are most interesting. A few of them are:
, i.e. the 3 numbers can be the lengths of the sides of a right triangle. Among these, the Primitive Pythagorean Triples, those in which the three numbers have no common divisor, are most interesting. A few of them are:
3-4-5
5-12-13
7-24-25
8-15-17
9-40-41









