Right triangle
A right triangle is any triangle with an angle of 90 degrees (that is, a right angle).
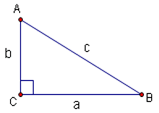
In the image above, you see that in triangle ![]() , angle C has a measure of 90 degrees, so
, angle C has a measure of 90 degrees, so ![]() is a right triangle. The sides of a right triangle have different names: The longest side, opposite the right angle, is called the hypotenuse. In the diagram, the hypotenuse is labelled c. The other two sides are called the legs of the triangle.
is a right triangle. The sides of a right triangle have different names: The longest side, opposite the right angle, is called the hypotenuse. In the diagram, the hypotenuse is labelled c. The other two sides are called the legs of the triangle.
Right triangles are very useful in geometry and for finding the areas of polygons. The most important relationship for right triangles is the Pythagorean Theorem. In addition, the field of trigonometry arises from the study of right triangles, and nearly all trigonometric identities can be deduced from them.
Special right triangles
There are several well-known right triangles which are easy to solve. These include the isosceles ![]() , where the hypotenuse is equal to
, where the hypotenuse is equal to ![]() times the length of either of the legs. The
times the length of either of the legs. The ![]() has sides in the ratio of
has sides in the ratio of ![]() .
.
If the lengths of the legs and hypotenuse are integral, then they form a Pythagorean triple.
Some well known Pythagorean triples include 3-4-5 ,5-12-13, 7-24-25, and others.
Properties
The area of the triangle can be calculated using half of the product of the lengths of the legs. It can also be calculated using half of the product of the median to the hypotenuse and the hypotenuse. Using similarity, it is possible to derive several formulas relating the sides, the hypotenuse, and median.
The circumradius is equal to half of the hypotenuse, or the median to the hypotenuse.