Difference between revisions of "Root-Mean Square-Arithmetic Mean-Geometric Mean-Harmonic mean Inequality"
m (Root-mean square-arithmetic mean-geometric mean-harmonic mean inequality moved to Root-Mean Square-Arithmetic Mean-Geometric Mean-Harmonic mean Inequality over redirect: revert) |
(cleanup) |
||
| Line 1: | Line 1: | ||
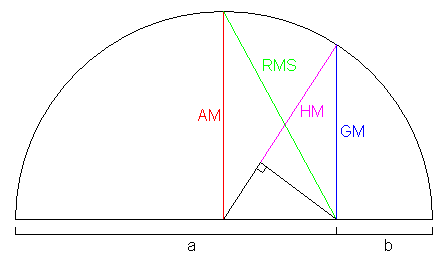
| − | The '''RMS-AM-GM-HM | + | The '''Root-Mean Square-Arithmetic Mean-Geometric Mean-Harmonic mean Inequality''' (RMS-AM-GM-HM), is an [[inequality]] of the [[root-mean square]], [[arithmetic mean]], [[geometric mean]], and [[harmonic mean]] of a set of [[positive]] [[real number]]s <math>x_1,\ldots,x_n</math> that says: |
<math>\sqrt{\frac{x_1^2+\cdots+x_n^2}{n}} \ge\frac{x_1+\cdots+x_n}{n}\ge\sqrt[n]{x_1\cdots x_n}\ge\frac{n}{\frac{1}{x_1}+\cdots+\frac{1}{x_n}}</math> | <math>\sqrt{\frac{x_1^2+\cdots+x_n^2}{n}} \ge\frac{x_1+\cdots+x_n}{n}\ge\sqrt[n]{x_1\cdots x_n}\ge\frac{n}{\frac{1}{x_1}+\cdots+\frac{1}{x_n}}</math> | ||
Revision as of 21:28, 20 December 2007
The Root-Mean Square-Arithmetic Mean-Geometric Mean-Harmonic mean Inequality (RMS-AM-GM-HM), is an inequality of the root-mean square, arithmetic mean, geometric mean, and harmonic mean of a set of positive real numbers 
that says:
![$\sqrt{\frac{x_1^2+\cdots+x_n^2}{n}} \ge\frac{x_1+\cdots+x_n}{n}\ge\sqrt[n]{x_1\cdots x_n}\ge\frac{n}{\frac{1}{x_1}+\cdots+\frac{1}{x_n}}$](http://latex.artofproblemsolving.com/c/e/b/ceb0cbb7b637caa6f14856d9350586808892e419.png)
with equality if and only if 
. This inequality can be expanded to the power mean inequality.
The inequality is clearly shown in this diagram for 
This article is a stub. Help us out by expanding it.
