Difference between revisions of "Squeeze Theorem"
(There's no need for the inequalities to be strict) |
(The old proof implicitly assumed that f converged. Replaced this with an epsilon-delta proof.) |
||
| Line 10: | Line 10: | ||
If <math>f(x)</math> is between <math>g(x)</math> and <math>h(x)</math> for all <math>x</math> in the neighborhood of <math>S</math>, then either <math>g(x)\leq f(x) \leq h(x)</math> or <math>h(x)\leq f(x)\leq g(x)</math> for all <math>x</math> in the neighborhood of <math>S</math>. Since the second case is basically the first case, we just need to prove the first case. | If <math>f(x)</math> is between <math>g(x)</math> and <math>h(x)</math> for all <math>x</math> in the neighborhood of <math>S</math>, then either <math>g(x)\leq f(x) \leq h(x)</math> or <math>h(x)\leq f(x)\leq g(x)</math> for all <math>x</math> in the neighborhood of <math>S</math>. Since the second case is basically the first case, we just need to prove the first case. | ||
| − | + | For all <math>\varepsilon >0</math>, we must prove that there is some <math>\delta > 0</math> for which <math>|x-S|<\delta \Rightarrow |f(x)-L|<\varepsilon</math>. | |
| + | |||
| + | Now since, <math>\lim_{x\to S}g(x)=\lim_{x\to S}h(x)=L</math>, there must exist <math>\delta_1,\delta_2>0</math> such that, | ||
| + | |||
| + | <math>|x-S|<\delta_1 \Rightarrow |g(x)-L|<\varepsilon</math> and, | ||
| + | |||
| + | <math>|x-S|<\delta_2 \Rightarrow |h(x)-L|<\varepsilon.</math> | ||
| + | |||
| + | Now let <math>\delta = \min\{\delta_1,\delta_2\}</math>. If <math>|x-S|<\delta</math>, then | ||
| + | |||
| + | <math>-\varepsilon < g(x) - L \leq f(x) - L \leq h(x) - L < \varepsilon.</math> | ||
| + | |||
| + | So <math>|f(x)-L|<\varepsilon</math>. Now by the definition of a limit, we get <math>\lim_{x\to S}f(x)=L</math>. | ||
==See Also== | ==See Also== | ||
Revision as of 21:52, 4 May 2008
| This is an AoPSWiki Word of the Week for May 4-11 |
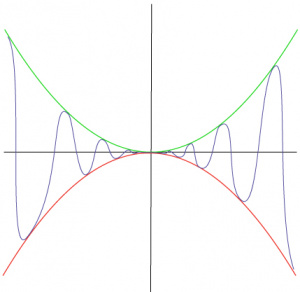
The Squeeze Theorem (also called the Sandwich Theorem or the Squeeze Play Theorem) is a relatively simple theorem that deals with calculus, specifically limits.
Theorem
Suppose 
is between 
and 
for all 
in the neighborhood of 
. If 
and 
approach some common limit L as approaches , then 
.
Proof
If is between and for all in the neighborhood of , then either 
or 
for all in the neighborhood of . Since the second case is basically the first case, we just need to prove the first case.
For all 
, we must prove that there is some 
for which 
.
Now since, 
, there must exist 
such that,
and,
Now let 
. If 
, then
So 
. Now by the definition of a limit, we get .
