Difference between revisions of "Squeeze Theorem"
m |
(There's no need for the inequalities to be strict) |
||
| Line 8: | Line 8: | ||
==Proof== | ==Proof== | ||
| − | If <math>f(x)</math> is between <math>g(x)</math> and <math>h(x)</math> for all <math>x</math> in the neighborhood of <math>S</math>, then either <math>g(x) | + | If <math>f(x)</math> is between <math>g(x)</math> and <math>h(x)</math> for all <math>x</math> in the neighborhood of <math>S</math>, then either <math>g(x)\leq f(x) \leq h(x)</math> or <math>h(x)\leq f(x)\leq g(x)</math> for all <math>x</math> in the neighborhood of <math>S</math>. Since the second case is basically the first case, we just need to prove the first case. |
If <math>g(x)</math> increases to <math>L</math>, then <math>f(x)</math> goes to either <math>L</math> or <math>M</math>, where <math>M>L</math>. If <math>h(x)</math> decreases to <math>L</math>, then <math>f(x)</math> goes to either <math>L</math> or <math>N</math>, where <math>N<L</math>. Since <math>f(x)</math> can't go to <math>M</math> or <math>N</math>, then <math>f(x)</math> must go to <math>L</math>. Therefore, <math>\lim_{x\to S}f(x)=L</math>. | If <math>g(x)</math> increases to <math>L</math>, then <math>f(x)</math> goes to either <math>L</math> or <math>M</math>, where <math>M>L</math>. If <math>h(x)</math> decreases to <math>L</math>, then <math>f(x)</math> goes to either <math>L</math> or <math>N</math>, where <math>N<L</math>. Since <math>f(x)</math> can't go to <math>M</math> or <math>N</math>, then <math>f(x)</math> must go to <math>L</math>. Therefore, <math>\lim_{x\to S}f(x)=L</math>. | ||
Revision as of 21:40, 4 May 2008
| This is an AoPSWiki Word of the Week for May 4-11 |
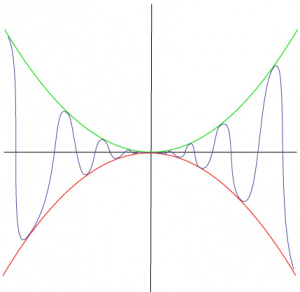
The Squeeze Theorem (also called the Sandwich Theorem or the Squeeze Play Theorem) is a relatively simple theorem that deals with calculus, specifically limits.
Theorem
Suppose 
is between 
and 
for all 
in the neighborhood of 
. If 
and 
approach some common limit L as approaches , then 
.
Proof
If is between and for all in the neighborhood of , then either 
or 
for all in the neighborhood of . Since the second case is basically the first case, we just need to prove the first case.
If increases to 
, then goes to either or 
, where 
. If decreases to , then goes to either or 
, where 
. Since can't go to or , then must go to . Therefore, .
