Squeeze Theorem
| This is an AoPSWiki Word of the Week for May 4-11 |
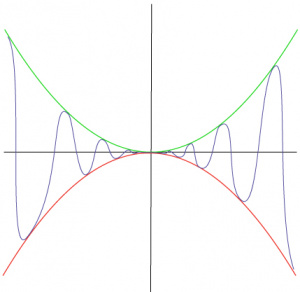
The Squeeze Theorem (also called the Sandwich Theorem or the Squeeze Play Theorem) is a relatively simple theorem that deals with calculus, specifically limits.
Theorem
Suppose ![]() is between
is between ![]() and
and ![]() for all
for all ![]() in the neighborhood of
in the neighborhood of ![]() . If
. If ![]() and
and ![]() approach some common limit L as
approach some common limit L as ![]() approaches
approaches ![]() , then
, then ![]() .
.
Proof
If ![]() is between
is between ![]() and
and ![]() for all
for all ![]() in the neighborhood of
in the neighborhood of ![]() , then either
, then either ![]() or
or ![]() for all
for all ![]() in the neighborhood of
in the neighborhood of ![]() . Since the second case is basically the first case, we just need to prove the first case.
. Since the second case is basically the first case, we just need to prove the first case.
For all ![]() , we must prove that there is some
, we must prove that there is some ![]() for which
for which ![]() .
.
Now since, ![]() , there must exist
, there must exist ![]() such that,
such that,
![]() and,
and,
![]()
Now let ![]() . If
. If ![]() , then
, then
![]()
So ![]() . Now by the definition of a limit, we get
. Now by the definition of a limit, we get ![]() .
.