Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Trigonometric identities"
(basic/reciprocal)
Line 1: Line 1:
−
Trigonometric identities are used to manipulate trig equations in certain ways.  Here is a list of them:
+
'''Trigonometric identities''' are used to manipulate trig equations in certain ways.  Here is a list of them:
  
 +
== Basic Definitions ==
 +
The six basic trigonometric functions can be defined using a right triangle:
  
−
== Reciprocal Identities ==
+
<center>[[Image:righttriangle.png]]</center>
 +
 
 +
The six trig functions are sine, cosine, tangent, cosecant, secant, and cotangent.  They are abbreviated by using the first three letters of their name (except for cosecant which uses <math>\csc</math>).  They are defined as follows:
 +
 
 +
{| style="width:75%; height:200px; margin: 1em auto 1em auto" border="0"
 +
|-
 +
| <math>\sin A = \frac ac</math> || <math>\csc A = \frac ca</math>
 +
|-
 +
| <math> \cos A = \frac bc</math> || <math>\sec A = \frac cb</math>
 +
|-
 +
| <math> \tan A = \frac ab</math> || <math> \cot A = \frac ba</math>
 +
|}
 +
 
 +
== Reciprocal Relations ==
 +
From the last section, it is easy to see that the following hold:
 +
 
 +
{| style="width:75%; margin: 1em auto 1em auto"
 +
|-
 +
| <math> \sin A = \frac 1{\csc A}</math> || <math> \cos A = \frac 1{\sec A}</math> || <math> \tan A = \frac 1{\cot A}</math>
 +
|}
  
 
== Pythagorean Identities ==
 
== Pythagorean Identities ==
Line 22: Line 43:
  
 
*<math>|1-e^{i\theta}|=2\sin\frac{\theta}{2}</math>
 
*<math>|1-e^{i\theta}|=2\sin\frac{\theta}{2}</math>
−
 
−
This page is incomplete--if you know of a trigonometric identity, add it.
 
  
 
==See also==
 
==See also==

Revision as of 08:34, 24 June 2006

Trigonometric identities are used to manipulate trig equations in certain ways. Here is a list of them:

Basic Definitions

The six basic trigonometric functions can be defined using a right triangle:

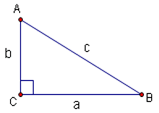
Righttriangle.png

The six trig functions are sine, cosine, tangent, cosecant, secant, and cotangent. They are abbreviated by using the first three letters of their name (except for cosecant which uses $\csc$). They are defined as follows:

$\sin A = \frac ac$ $\csc A = \frac ca$
$\cos A = \frac bc$ $\sec A = \frac cb$
$\tan A = \frac ab$ $\cot A = \frac ba$

Reciprocal Relations

From the last section, it is easy to see that the following hold:

$\sin A = \frac 1{\csc A}$ $\cos A = \frac 1{\sec A}$ $\tan A = \frac 1{\cot A}$

Pythagorean Identities

  • $\displaystyle \sin^2x + \cos^2x = 1$
  • $\displaystyle 1 + \cot^2x = \csc^2x$
  • $\displaystyle \tan^2x + 1 = \sec^2x$

Angle Addition Identities

  • $\displaystyle \sin \theta \cos \gamma + \sin \gamma \cos \theta = \sin \left(\theta+\gamma\right)$
  • $\displaystyle \cos \theta \cos \gamma - \sin theta \sin gamma = \cos \left(\theta+\gamma\right)$
  • $\displaystyle \frac{\tan \theta + \tan gamma}{1-\tan\theta\tan\gamma}=\tan\left(\theta+\gamma\right)$

Even-Odd Identities

Prosthaphaersis Indentities

(Otherwise known as sum-to-product identities)

Other Identities

  • $|1-e^{i\theta}|=2\sin\frac{\theta}{2}$

See also

This article is a stub. Help us out by expanding it.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Trigonometric_identities&oldid=4452"