Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Trigonometric identities"

(Pythagorean identities)
(double/half angle)
Line 39: Line 39:
 
|}
 
|}
  
−
== Angle Addition Identities ==
+
== Angle Addition/Subtraction Identities ==
−
*<math>\displaystyle \sin \theta \cos \gamma + \sin \gamma \cos \theta = \sin \left(\theta+\gamma\right)</math>
+
Once we have formulas for angle addition, angle subtraction is rather easy to derive.  For example, we just look at <math> \sin(\alpha+(-\beta))</math> and we can derive the sine angle subtraction formula using the sine angle addition formula.
−
*<math>\displaystyle \cos \theta \cos \gamma - \sin theta \sin \gamma = \cos \left(\theta+\gamma\right)</math>
 
−
*<math>\displaystyle \frac{\tan \theta + \tan \gamma}{1-\tan\theta\tan\gamma}=\tan\left(\theta+\gamma\right)</math>
 
  
 +
{| style="width:100%; height:130px; margin: 1em auto 1em auto"
 +
|-
 +
| <math> \sin(\alpha + \beta) = \sin \alpha\cos \beta +\sin \beta \cos \alpha</math> || <math> \sin(\alpha - \beta) = \sin \alpha \cos \beta - \sin \beta \cos \alpha</math>
 +
|-
 +
| <math> \cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta </math> || <math> \cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta</math>
 +
|-
 +
| <math> \tan(\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1-\tan \alpha \tan \beta} </math> || <math> \tan(\alpha - \beta) = \frac{\tan \alpha - \tan \beta}{1+\tan \alpha \tan \beta} </math>
 +
|}
 +
 +
== Double/Half Angle Identities ==
 +
Double angle identities are easily derived from the angle addition formulas by just letting <math> \alpha = \beta </math>.  Doing so yields:
 +
 +
{| style="height:200px; margin: 1em auto 1em auto"
 +
|-
 +
| <math> \sin 2\alpha </math> || = || <math>2\sin \alpha \cos \alpha</math>
 +
|-
 +
| <math> \cos 2\alpha </math> || = || <math> \cos^2 \alpha - \sin^2 \alpha</math>
 +
|-
 +
| || = || <math> 2\cos^2 \alpha - 1</math>
 +
|-
 +
| || = || <math> 1-2\sin^2 \alpha</math>
 +
|-
 +
| <math> \tan 2\alpha </math> || = || <math>\frac{2\tan \alpha}{1-\tan^2\alpha} </math>
 +
|}
 
== Even-Odd Identities ==
 
== Even-Odd Identities ==
  

Revision as of 09:22, 24 June 2006

Trigonometric identities are used to manipulate trig equations in certain ways. Here is a list of them:

Basic Definitions

The six basic trigonometric functions can be defined using a right triangle:

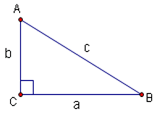
Righttriangle.png

The six trig functions are sine, cosine, tangent, cosecant, secant, and cotangent. They are abbreviated by using the first three letters of their name (except for cosecant which uses $\csc$). They are defined as follows:

$\sin A = \frac ac$ $\csc A = \frac ca$
$\cos A = \frac bc$ $\sec A = \frac cb$
$\tan A = \frac ab$ $\cot A = \frac ba$

Reciprocal Relations

From the last section, it is easy to see that the following hold:

$\sin A = \frac 1{\csc A}$ $\cos A = \frac 1{\sec A}$ $\tan A = \frac 1{\cot A}$

Another useful identity that isn't a reciprocal relation is that $\tan A =\frac{\sin A}{\cos A}$.

Pythagorean Identities

Using the Pythagorean Theorem on our triangle above, we know that $\displaystyle a^2 + b^2 = c^2$. If we divide by $c^2$ we get $\left(\frac ac\right)^2 + \left(\frac bc\right)^2 = 1$ which is just $\sin^2 A + \cos^2 A =1$. Dividing by $a^2$ or $b^2$ instead produces two other similar identities. The Pythagorean Identities are listed below:

$\displaystyle \sin^2x + \cos^2x = 1$
$\displaystyle 1 + \cot^2x = \csc^2x$
$\displaystyle \tan^2x + 1 = \sec^2x$

Angle Addition/Subtraction Identities

Once we have formulas for angle addition, angle subtraction is rather easy to derive. For example, we just look at $\sin(\alpha+(-\beta))$ and we can derive the sine angle subtraction formula using the sine angle addition formula.

$\sin(\alpha + \beta) = \sin \alpha\cos \beta +\sin \beta \cos \alpha$ $\sin(\alpha - \beta) = \sin \alpha \cos \beta - \sin \beta \cos \alpha$
$\cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta$ $\cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta$
$\tan(\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1-\tan \alpha \tan \beta}$ $\tan(\alpha - \beta) = \frac{\tan \alpha - \tan \beta}{1+\tan \alpha \tan \beta}$

Double/Half Angle Identities

Double angle identities are easily derived from the angle addition formulas by just letting $\alpha = \beta$. Doing so yields:

$\sin 2\alpha$ = $2\sin \alpha \cos \alpha$
$\cos 2\alpha$ = $\cos^2 \alpha - \sin^2 \alpha$
= $2\cos^2 \alpha - 1$
= $1-2\sin^2 \alpha$
$\tan 2\alpha$ = $\frac{2\tan \alpha}{1-\tan^2\alpha}$

Even-Odd Identities

Prosthaphaersis Indentities

(Otherwise known as sum-to-product identities)

Other Identities

  • $|1-e^{i\theta}|=2\sin\frac{\theta}{2}$

See also

This article is a stub. Help us out by expanding it.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Trigonometric_identities&oldid=4460"