User:Rowechen
Hey how did you get to this page? If you aren't me then I have to say hello. If you are me then I must be pretty conceited to waste my time looking at my own page. If you aren't me, seriously, how did you get to this page? This is pretty cool. Well, nice meeting you! I'm going to stop wasting my time typing this up and do some math. Gtg. Bye.
Here's the AIME compilation I will be doing:
Contents
Problem 3
By a proper divisor of a natural number we mean a positive integral divisor other than 1 and the number itself. A natural number greater than 1 will be called "nice" if it is equal to the product of its distinct proper divisors. What is the sum of the first ten nice numbers?
Problem 4
Let ![]() be a list of positive integers - not necessarily distinct - in which the number
be a list of positive integers - not necessarily distinct - in which the number ![]() appears. The arithmetic mean of the numbers in
appears. The arithmetic mean of the numbers in ![]() is
is ![]() . However, if
. However, if ![]() is removed, the arithmetic mean of the numbers is
is removed, the arithmetic mean of the numbers is ![]() . What's the largest number that can appear in
. What's the largest number that can appear in ![]() ?
?
Problem 6
Rectangle ![]() is divided into four parts of equal area by five segments as shown in the figure, where
is divided into four parts of equal area by five segments as shown in the figure, where ![]() , and
, and ![]() is parallel to
is parallel to ![]() . Find the length of
. Find the length of ![]() (in cm) if
(in cm) if ![]() cm and
cm and ![]() cm.
cm.
Problem 8
What is the largest ![]() -digit prime factor of the integer
-digit prime factor of the integer  ?
?
Problem 7
The increasing sequence ![]() consists of all those positive integers which are powers of 3 or sums of distinct powers of 3. Find the
consists of all those positive integers which are powers of 3 or sums of distinct powers of 3. Find the ![]() term of this sequence.
term of this sequence.
Problem 10
The numbers ![]() ,
, ![]() and
and ![]() have something in common: each is a
have something in common: each is a ![]() -digit number beginning with
-digit number beginning with ![]() that has exactly two identical digits. How many such numbers are there?
that has exactly two identical digits. How many such numbers are there?
Problem 8
What is the largest positive integer ![]() for which there is a unique integer
for which there is a unique integer ![]() such that
such that ![]() ?
?
Problem 12
Diameter ![]() of a circle has length a
of a circle has length a ![]() -digit integer (base ten). Reversing the digits gives the length of the perpendicular chord
-digit integer (base ten). Reversing the digits gives the length of the perpendicular chord ![]() . The distance from their intersection point
. The distance from their intersection point ![]() to the center
to the center ![]() is a positive rational number. Determine the length of
is a positive rational number. Determine the length of ![]() .
.
Problem 10
Let ![]() ,
, ![]() ,
, ![]() be the three sides of a triangle, and let
be the three sides of a triangle, and let ![]() ,
, ![]() ,
, ![]() , be the angles opposite them. If
, be the angles opposite them. If ![]() , find
, find
Problem 11
A sample of 121 integers is given, each between 1 and 1000 inclusive, with repetitions allowed. The sample has a unique mode (most frequent value). Let ![]() be the difference between the mode and the arithmetic mean of the sample. What is the largest possible value of
be the difference between the mode and the arithmetic mean of the sample. What is the largest possible value of ![]() ? (For real
? (For real ![]() ,
, ![]() is the greatest integer less than or equal to
is the greatest integer less than or equal to ![]() .)
.)
Problem 13
In a sequence of coin tosses, one can keep a record of instances in which a tail is immediately followed by a head, a head is immediately followed by a head, and etc. We denote these by TH, HH, and etc. For example, in the sequence TTTHHTHTTTHHTTH of 15 coin tosses we observe that there are two HH, three HT, four TH, and five TT subsequences. How many different sequences of 15 coin tosses will contain exactly two HH, three HT, four TH, and five TT subsequences?
Problem 15
Determine ![]() if
if
Problem 15
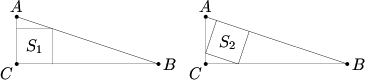
Squares ![]() and
and ![]() are inscribed in right triangle
are inscribed in right triangle ![]() , as shown in the figures below. Find
, as shown in the figures below. Find ![]() if area
if area ![]() and area
and area ![]() .
.
Problem 13
A given sequence ![]() of distinct real numbers can be put in ascending order by means of one or more "bubble passes". A bubble pass through a given sequence consists of comparing the second term with the first term, and exchanging them if and only if the second term is smaller, then comparing the third term with the second term and exchanging them if and only if the third term is smaller, and so on in order, through comparing the last term,
of distinct real numbers can be put in ascending order by means of one or more "bubble passes". A bubble pass through a given sequence consists of comparing the second term with the first term, and exchanging them if and only if the second term is smaller, then comparing the third term with the second term and exchanging them if and only if the third term is smaller, and so on in order, through comparing the last term, ![]() , with its current predecessor and exchanging them if and only if the last term is smaller.
, with its current predecessor and exchanging them if and only if the last term is smaller.
The example below shows how the sequence 1, 9, 8, 7 is transformed into the sequence 1, 8, 7, 9 by one bubble pass. The numbers compared at each step are underlined.
Suppose that ![]() , and that the terms of the initial sequence
, and that the terms of the initial sequence ![]() are distinct from one another and are in random order. Let
are distinct from one another and are in random order. Let ![]() , in lowest terms, be the probability that the number that begins as
, in lowest terms, be the probability that the number that begins as ![]() will end up, after one bubble pass, in the
will end up, after one bubble pass, in the ![]() place. Find
place. Find ![]() .
.
Problem 15
Let triangle ![]() be a right triangle in the
be a right triangle in the ![]() -plane with a right angle at
-plane with a right angle at ![]() . Given that the length of the hypotenuse
. Given that the length of the hypotenuse ![]() is
is ![]() , and that the medians through
, and that the medians through ![]() and
and ![]() lie along the lines
lie along the lines ![]() and
and ![]() respectively, find the area of triangle
respectively, find the area of triangle ![]() .
.