1973 IMO Problems/Problem 3
Problem
Let ![]() and
and ![]() be real numbers for which the equation
be real numbers for which the equation
![]() has at least one real solution. For all such pairs
has at least one real solution. For all such pairs ![]() , find the minimum value of
, find the minimum value of ![]() .
.
Solution
Substitute ![]() to change the original equation into
to change the original equation into ![]() . This equation has solutions
. This equation has solutions ![]() . We also know that
. We also know that
![]()
So,
![\[\left | \frac{-a \pm \sqrt{a^2+8-4b}}{2} \right | \geq 2\ \ \ \ \ \ \ \ (2)\]](http://latex.artofproblemsolving.com/3/3/4/3348efe53ea0d034ce5d21c5f5a8b37d4579de12.png)
![]()
![]()
Rearranging and squaring both sides,
![]()
![]()
So,
![]()
![]() .
.
Therefore, the smallest possible value of ![]() is
is ![]() , when
, when ![]() and
and ![]() .
.
Borrowed from [1]
Remarks (added by pf02, June 2025)
1. The solution above is incomplete and it has some serious errors. The result is correct, but the method for obtaining it is flawed. For the sake of reference to the steps in the solution I added labels, but I did not make any changes to the solution. I will highlight the errors and the missing steps:
A. (1) is true when we know that ![]() is real. By hypothesis the
equation has at least one real solution, so (1) is true for this
solution. A necessary condition for this is that
is real. By hypothesis the
equation has at least one real solution, so (1) is true for this
solution. A necessary condition for this is that
![]() . We have to use this in the proof, or if we
obtain a result without having used it, we need to verify that the
result satisfies this condition. This is missing from the solution.
. We have to use this in the proof, or if we
obtain a result without having used it, we need to verify that the
result satisfies this condition. This is missing from the solution.
B. (2) is equivalent to (3) when ![]() is interpreted as an
is interpreted as an
![]() . (If the
. (If the ![]() would be an
would be an ![]() then (2) and (3) would not be equivalent.) In our problem the
then (2) and (3) would not be equivalent.) In our problem the
![]() is an
is an ![]() so the proof can proceed. However,
while easy, going from (2) to (3) is not obvious, and it is an
important step in the proof, so it should be explained.
so the proof can proceed. However,
while easy, going from (2) to (3) is not obvious, and it is an
important step in the proof, so it should be explained.
C. There is a small computational error in (4): we should have
![]() , not
, not ![]() . This error is in writing, the computation
proceeds as if it did not happen.
. This error is in writing, the computation
proceeds as if it did not happen.
D. Going from (5) to (6) is a very serious error. Replacing
![]() by
by ![]() can be done only when certain conditions
are satisfied (for example if we know that
can be done only when certain conditions
are satisfied (for example if we know that ![]() and
and
![]() or if we know that
or if we know that ![]() ). So
writing down (6) is completely unjustified.
). So
writing down (6) is completely unjustified.
2. I will not take the task of fixing this solution. Instead, I will give a different solution below.
Solution 2
The plan of this solution is the following: we will consider
the plane of coordinates ![]() . We will write the condition(s)
for the equation to have at least one real solution. These will
be inequalities in
. We will write the condition(s)
for the equation to have at least one real solution. These will
be inequalities in ![]() , which delimit regions in the
, which delimit regions in the ![]() plane.
plane. ![]() represents the square of the distance from
the point of coordinates
represents the square of the distance from
the point of coordinates ![]() to the origin. We will find
the point(s) in the region we delimited which are closest to the
origin. These are minimizing
to the origin. We will find
the point(s) in the region we delimited which are closest to the
origin. These are minimizing ![]() .
.
Dividing the given equation by ![]() and making the substitution
and making the substitution
![]() , we can re-write the given equation as
, we can re-write the given equation as
![]() . The given equation has at least one
real root when this equation in
. The given equation has at least one
real root when this equation in ![]() has real roots. This is
true when
has real roots. This is
true when ![]() . This represents the parabola
. This represents the parabola
![]() in the
in the ![]() plane. Refer to this
parabola as
plane. Refer to this
parabola as ![]() .
.
The two solutions of the equation in ![]() are
are
![]() . We will take them one
at a time, and write down the conditions for its solution
. We will take them one
at a time, and write down the conditions for its solution ![]() to be real. Start with the
to be real. Start with the ![]() sign, and consider the equation
sign, and consider the equation
![]()
This equation has real solutions when
![]() . Work out the square,
rearrange terms and simplify. We get
. Work out the square,
rearrange terms and simplify. We get
![]() .
.
Note that at this point we could continue working with inequalities,
being vary careful in considering all the cases as we do computations.
Instead, we will consider the equation
![]() . This is a curve in the
. This is a curve in the
![]() plane, delimiting several regions in the plane. We will
study the curve, and decide which are the regions in the
plane, delimiting several regions in the plane. We will
study the curve, and decide which are the regions in the ![]() plane in which the inequality is true. This will give us a set
of points
plane in which the inequality is true. This will give us a set
of points ![]() for which the equation has at least one real
root.
for which the equation has at least one real
root.
Square both sides and rearrange terms. We get ![]() .
As a curve, this is two lines
.
As a curve, this is two lines ![]() with equations
with equations
![]() and
and ![]() . Before proceeding, we have
to verify the validity of these solutions since we may have
introduced "fake" solutions when we squared both sides.
. Before proceeding, we have
to verify the validity of these solutions since we may have
introduced "fake" solutions when we squared both sides.
Plug ![]() into
into ![]() .
We get
.
We get ![]() . This is true when
. This is true when
![]() or
or ![]() . Thus,
. Thus, ![]() is valid when
is valid when
![]() .
.
Similarly, plug ![]() into
into
![]() , and get that
, and get that ![]() is valid when
is valid when ![]() .
.
The parabola ![]() , the lines
, the lines ![]() and the lines
and the lines ![]() carve the
carve the ![]() plane into several regions. We now have to
verify which are the regions in which
plane into several regions. We now have to
verify which are the regions in which
![]() . While mildly tedious,
this is very easy: we just have to take a numerical sample in each
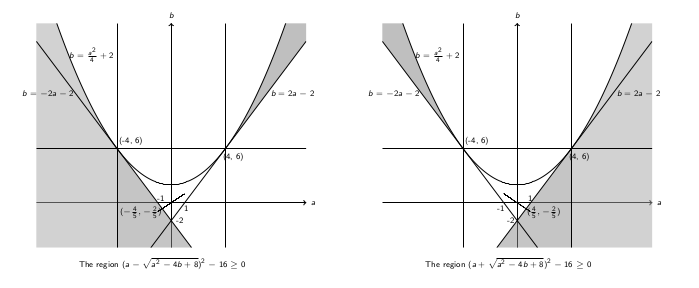
region and verify the inequality. The results are shown in the
image below (the one on the left): if the point
. While mildly tedious,
this is very easy: we just have to take a numerical sample in each
region and verify the inequality. The results are shown in the
image below (the one on the left): if the point ![]() is in
the shaded area, then the inequality is satisfied, so equation
in the problem has at least one real solution.
is in
the shaded area, then the inequality is satisfied, so equation
in the problem has at least one real solution.
Now take the ![]() sign from
sign from ![]() .
We get the equation
.
We get the equation ![]() .
This has real solutions when
.
This has real solutions when ![]() .
Consider the regions delimited by
.
Consider the regions delimited by
![]() , and find the regions when
the inequality is true. The computations are very similar to the
ones in the preceding case. The regions for
, and find the regions when
the inequality is true. The computations are very similar to the
ones in the preceding case. The regions for ![]() which guarantee
that the equation from the problem has at least one real solution
are shown in the image above (the one on the right hand side).
which guarantee
that the equation from the problem has at least one real solution
are shown in the image above (the one on the right hand side).
It is now clear that the points ![]() in these regions closest
to
in these regions closest
to ![]() are the ones at the intersection of the line
are the ones at the intersection of the line ![]() with the perpendicular from
with the perpendicular from ![]() , and at the intersection of
the line
, and at the intersection of
the line ![]() with the perpendicular from
with the perpendicular from ![]() . A
very simple computation shows that these points are
. A
very simple computation shows that these points are
![]() .
Then the square of the distance from
.
Then the square of the distance from ![]() to these points
to these points
![]() .
.
[Solution by pf02, June 2025]
See Also
| 1973 IMO (Problems) • Resources | ||
| Preceded by Problem 2 |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 4 |
| All IMO Problems and Solutions | ||