2005 AMC 10A Problems/Problem 19

Problem

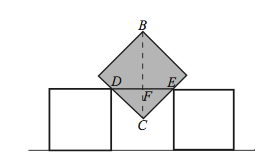
Three one-inch squares are placed with their bases on a line. The center square is lifted out and rotated $45^{\circ}$ , as shown. Then it is centered and lowered into its original location until it touches both of the adjoining squares. How many inches is the point $B$ from the line on which the bases of the original squares were placed?

$[asy] unitsize(1inch); defaultpen(linewidth(.8pt)+fontsize(8pt)); draw((0,0)--((1/3) + 3*(1/2),0)); fill(((1/6) + (1/2),0)--((1/6) + (1/2),(1/2))--((1/6) + 1,(1/2))--((1/6) + 1,0)--cycle, rgb(.7,.7,.7)); draw(((1/6),0)--((1/6) + (1/2),0)--((1/6) + (1/2),(1/2))--((1/6),(1/2))--cycle); draw(((1/6) + (1/2),0)--((1/6) + (1/2),(1/2))--((1/6) + 1,(1/2))--((1/6) + 1,0)--cycle); draw(((1/6) + 1,0)--((1/6) + 1,(1/2))--((1/6) + (3/2),(1/2))--((1/6) + (3/2),0)--cycle); draw((2,0)--(2 + (1/3) + (3/2),0)); draw(((2/3) + (3/2),0)--((2/3) + 2,0)--((2/3) + 2,(1/2))--((2/3) + (3/2),(1/2))--cycle); draw(((2/3) + (5/2),0)--((2/3) + (5/2),(1/2))--((2/3) + 3,(1/2))--((2/3) + 3,0)--cycle); label("$B$",((1/6) + (1/2),(1/2)),NW); label("$B$",((2/3) + 2 + (1/4),(29/30)),NNE); draw(((1/6) + (1/2),(1/2)+0.05)..(1,.8)..((2/3) + 2 + (1/4)-.05,(29/30)),EndArrow(HookHead,3)); fill(((2/3) + 2 + (1/4),(1/4))--((2/3) + (5/2) + (1/10),(1/2) + (1/9))--((2/3) + 2 + (1/4),(29/30))--((2/3) + 2 - (1/10),(1/2) + (1/9))--cycle, rgb(.7,.7,.7)); draw(((2/3) + 2 + (1/4),(1/4))--((2/3) + (5/2) + (1/10),(1/2) + (1/9))--((2/3) + 2 + (1/4),(29/30))--((2/3) + 2 - (1/10),(1/2) + (1/9))--cycle);[/asy]$

$\textbf{(A)}\ 1\qquad\textbf{(B)}\ \sqrt{2}\qquad\textbf{(C)}\ \frac{3}{2}\qquad\textbf{(D)}\ \sqrt{2}+\frac{1}{2}\qquad\textbf{(E)}\ 2$

Solution

The rotated middle square is lowered until it touches both the adjoining squares, so since the horizontal distance between those squares is $1$ inch, the middle square will stop being lowered once the length $DE$ in the diagram below is $1$ inch. Now, since $DC$ and $EC$ respectively pass through the vertices $D$ and $E$ of the horizontal middle square, and intersect at right angles, they must be the diagonals of the horizontal middle square, so $\triangle DEC$ is a $45^{\circ}-45^{\circ}-90^{\circ}$ triangle.

It follows that when $DE = 1$ , we have $DC = EC = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$ , and as the middle square was rotated by exactly $45^{\circ}$ from its original horizontal position, the diagonal $BC$ is now vertical, giving $BC \perp DE$ . This means $\triangle DFC$ and $\triangle EFC$ are also $45^{\circ}-45^{\circ}-90^{\circ}$ triangles, and hence $FC = \frac{\left(\frac{\sqrt{2}}{2}\right)}{\sqrt{2}} = \frac{1}{2}$ .

Lastly, since $BC$ is the diagonal of a unit square, its length is $\sqrt{1^2+1^2} = \sqrt{2}$ (by Pythagoras' theorem), so we deduce that the distance from $B$ to the bottom horizontal line is

$BC-FC+1 = \sqrt{2}-\frac{1}{2}+1=\boxed{\textbf{(D) }\sqrt{2}+\dfrac{1}{2}}.$

(An alternative for this last step is to compute the distance from $C$ to the bottom horizontal line as $1-FC = 1-\frac{1}{2} = \frac{1}{2}$ , so that the distance from $B$ to the bottom horizontal line is, once again, $BC+\frac{1}{2} = \boxed{\textbf{(D) } \sqrt{2}+\frac{1}{2}}$ .)

2005 AMC 10A (Problems • Answer Key • Resources)
Preceded by Problem 18	Followed by Problem 20
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

Page

Toolbox

Search

2005 AMC 10A Problems/Problem 19

Problem

Solution

See Also