Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2005 AMC 10A Problems/Problem 20

Problem

An equiangular octagon has four sides of length $1$ and four sides of length $\sqrt{2}/2$, arranged so that no two consecutive sides have the same length. What is the area of the octagon?

$\textbf{(A) } \frac{7}{2}\qquad \textbf{(B) } \frac{7\sqrt{2}}{2}\qquad \textbf{(C) } \frac{5+4\sqrt{2}}{2}\qquad \textbf{(D) } \frac{4+5\sqrt{2}}{2}\qquad \textbf{(E) } 7$

Solution 1

The sum of the octagon's angles is $180\cdot(8-2)^{\circ} = 1080^{\circ}$, so since it is equiangular, each angle is $\frac{1080^{\circ}}{8} = 135^{\circ}$, i.e. the same as in a regular octagon. This means that this octagon, just like with a regular octagon, can be divided into squares (whose diagonals form $45^{\circ}$ angles) and right triangles.

In particular, as shown in the diagram below, the area of this octagon can be divided up into $5$ squares of side length $\frac{\sqrt{2}}{2}$ and $4$ right triangles, each of which has half the area of each of the squares (since each square has diagonal $\frac{\sqrt{2}}{2} \cdot \sqrt{2} = 1$, so each right triangle is congruent by side-side-side to one of the triangles formed by slicing a square along one of its diagonals).

Therefore, the area of the octagon is equal to the area of $5 + 4 \cdot \frac{1}{2} = 7$ of the squares, and the area of each square is simply $\left(\frac{\sqrt{2}}{2}\right)^2 = \frac{1}{2}$, so the answer is is $7 \cdot \frac{1}{2} = \boxed{\textbf{(A) } \frac{7}{2}}$.

[asy] pair A=(0.5, 0), B=(0, 0.5), C=(0, 1.5), D=(0.5, 2), E=(1.5, 2), F=(2, 1.5), G=(2, 0.5), H=(1.5, 0); draw(A--B); draw(B--C); draw(C--D); draw(D--E);draw(E--F);draw(F--G); draw(G--H); draw(H--A);draw(A--F, blue);draw(E--B,blue);draw(C--H, blue); draw(D--G,blue);dot(A);dot(B);dot(C);dot(D);dot(E);dot(F);dot(G);dot(H); [/asy]

Solution 2

Using the same diagram as in Solution 1, we can extend the sides of length $1$ to form a bounding square around the octagon, with the region inside the square but outside the octagon consisting of $4$ right triangles. (We could also extend the sides of length $\frac{\sqrt{2}}{2}$ to give a similar bounding square, but this would make the computations slightly harder.)

As in Solution 1, since all the interior angles of the octagon are $135^{\circ}$, the right triangles are all $45^{\circ}-45^{\circ}-90^{\circ}$ triangles with hypotenuse $\frac{\sqrt{2}}{2}$. Thus the length of their other legs is $\frac{\left(\frac{\sqrt{2}}{2}\right)}{\sqrt{2}} = \frac{1}{2}$, so the bounding square has total side length $1 + 2 \cdot \frac{1}{2} = 2$, and hence area $2^2 = 4$. Each of the right triangles has area $\frac{1}{2} \cdot \left(\frac{1}{2}\right)^2 = \frac{1}{8}$, so we deduce that the area of the octagon is $4 - 4 \cdot \frac{1}{8} = \boxed{\textbf{(A) } \frac{7}{2}}$.

edited by mobius247

Solution 3

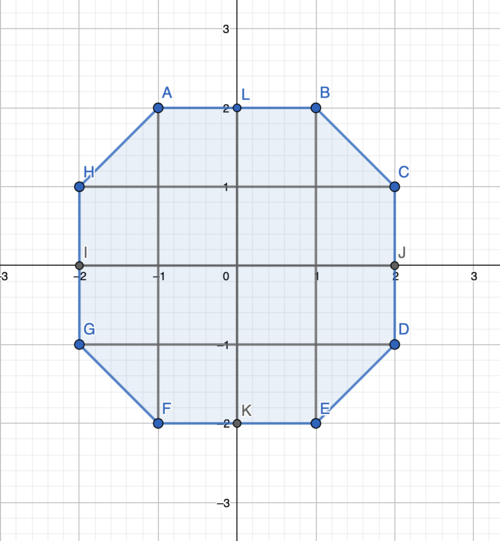
As shown in the diagram below, we can also divide the octagon into squares and right triangles using horizontal and vertical lines, rather than the lines at a $45^{\circ}$ angle that were used in Solutions 1 and 2.

AMC10 2005A P20.png

(Diagram made using Geogebra)

For the same reasons as in Solutions 1 and 2, the octagon's $135^{\circ}$ interior angles mean that the right triangles are $45^{\circ}-45^{\circ}-90^{\circ}$ triangles with hypotenuse $\frac{\sqrt{2}}{2}$, so their other legs have length $\frac{\left(\frac{\sqrt{2}}{2}\right)}{\sqrt{2}} = \frac{1}{2}$. Accordingly, their areas are each $\frac{1}{2} \cdot \left(\frac{1}{2}\right)^2 = \frac{1}{8}$, while by symmetry, each of the squares also has side length $\frac{1}{2}$, and thus area $\left(\frac{1}{2}\right)^2 = \frac{1}{4}$.

Hence, as the octagon consists of $12$ squares and $4$ right triangles, its total area is $12\cdot\frac{1}{4}+4\cdot\frac{1}{8} = \boxed{\textbf{(A) } \frac{7}{2}}$.

~JH. L

Video Solution

https://youtu.be/rwPFZnYk9V8

See Also

2005 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 19 		Followed by
Problem 21
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2005_AMC_10A_Problems/Problem_20&oldid=253110"