Angle bisector
| This is an AoPSWiki Word of the Week for June 6-12 |
Contents
[hide]Angle Bisector
For an angle ![]() , the (internal) angle bisector of
, the (internal) angle bisector of ![]() is the line from
is the line from ![]() such that the angle between this line and
such that the angle between this line and ![]() is congruent to the angle between this line and
is congruent to the angle between this line and ![]() :
:
An angle ![]() also has an external angle bisector, which bisects external angle
also has an external angle bisector, which bisects external angle ![]() :
:
![[asy] import markers; pair A,B,C,D,E,F; B=(0,0); C=(5,0); A=(4,2); D=(3,4); E=(10/3,0); F=rotate(-90,A)*(E); draw(A--B--C--cycle,blue); draw(C--D,blue); pen p=blue+0.15mm; draw(A--F,p); dot(A^^B^^C,red); label("$A$",A,NE); label("$B$",B,W); label("$C$",C,E); markangle(n=1,radius=20,D,A,F,green); markangle(n=1,radius=22,F,A,B,green); [/asy]](http://latex.artofproblemsolving.com/2/f/5/2f50679988883833282611240be251280d884bc4.png)
The external angle is defined by
![]() and the two angle bisectors are perpendicular to each other.
and the two angle bisectors are perpendicular to each other.
Features of Angle Bisectors
- The distances from a point on an angle bisector to both of its sides are equal.
- The angle bisectors are the locus of points which are equidistant from the two sides of the angle.
- A reflection about either angle bisector maps the two sides of the angle to each other.
- In a triangle, the Angle Bisector Theorem gives the ratio in which the angle bisector cuts the opposite side.
- In a triangle, the internal angle bisectors (which are cevians) all intersect at the incenter of the triangle. The internal angle bisector of one angle and the external angle bisectors of the other two angles all intersect at an excenter of the triangle.
- A bisector of an angle can be constructed using a compass and straightedge.
|
|
| Triangle |
Proofs
Angle Bisector Locus Theorem
Theorem: A point lies on the internal angle bisector of ![]() if and only if it is equidistant from the sides
if and only if it is equidistant from the sides ![]() and
and ![]() .
.
Proof:
Let point ![]() lie on the angle bisector of
lie on the angle bisector of ![]() . Drop perpendiculars from
. Drop perpendiculars from ![]() to lines
to lines ![]() and
and ![]() , meeting them at points
, meeting them at points ![]() and
and ![]() respectively.
respectively.
Since
![]() and both triangles
and both triangles ![]() and
and ![]() are right triangles with a shared hypotenuse
are right triangles with a shared hypotenuse ![]() and equal angles, they are congruent by AAS. Hence,
and equal angles, they are congruent by AAS. Hence,
![]()
Conversely, if ![]() is equidistant from
is equidistant from ![]() and
and ![]() , then
, then ![]() , and
, and ![]() lies on the angle bisector of
lies on the angle bisector of ![]() .
.
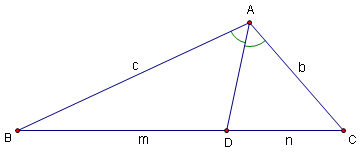
Angle Bisector Theorem
Theorem: In triangle ![]() , if the internal angle bisector of
, if the internal angle bisector of ![]() intersects
intersects ![]() at point
at point ![]() , then
, then
![]()
Proof:
Let ![]() , and draw the angle bisector
, and draw the angle bisector ![]() .
.
Construct a line through ![]() parallel to
parallel to ![]() , and let it intersect the extension of
, and let it intersect the extension of ![]() at point
at point ![]() .
.
Since
![]() (by alternate interior angles), triangles
(by alternate interior angles), triangles ![]() and
and ![]() are similar by AA.
are similar by AA.
Therefore,
![]()
Internal and External Angle Bisectors Are Perpendicular
Theorem: The internal and external angle bisectors of any angle are perpendicular.
Proof:
Let the internal and external angle bisectors divide ![]() and its supplement into two equal parts.
and its supplement into two equal parts.
The internal angle is ![]() , and the external angle is
, and the external angle is ![]() .
.
So the internal bisector makes an angle of ![]() with one side, and the external bisector makes an angle of
with one side, and the external bisector makes an angle of ![]() with the same side. Adding them:
with the same side. Adding them:
![]() so the two bisectors are perpendicular.
so the two bisectors are perpendicular.





![[asy] size(300); import markers; pair excenter(pair A, pair B, pair C){ pair X, Z; X=A+expi((angle(A-B)+angle(C-A))/2); Z=C+expi((angle(C-B)+angle(A-C))/2); return extension(X,A,Z,C); } pair X=(0,0), Y=(-10,0), Z=(-3,6); pair exX=excenter(Z,X,Y), exY=excenter(X,Y,Z), exZ=excenter(Y,Z,X); label("X",X,2*(1.5,-1));label("Y",Y,2*(-3,-1));label("Z",Z,(0.6,2)); dot(X^^Y^^Z); draw(0.3*(X-Y)+X--Y+0.3*(Y-X));draw(0.3*(Y-Z)+Y--Z+0.3*(Z-Y));draw(0.3*(X-Z)+X--Z+0.3*(Z-X)); draw(X+0.3*(X-exX)--exX,orange);draw(Y+0.3*(Y-exY)--exY,orange);draw(Z+0.3*(Z-exZ)--0.6*(exZ-Z)+Z,orange); draw(Y-0.5*(exX-Y)--Y+0.5*(exX-Y),green);draw(Z-0.5*(exX-Z)--Z+0.5*(exX-Z),green);draw(X-0.5*(exY-X)--X+0.5*(exY-X),green); pair I=extension(X,exX,Z,exZ); dot("I",I,(-1,2)); draw(circle(I,length(I-foot(I,X,Y))),blue); markangle(n=1,3*(Z-X)+X,Z,exX,radius=22,marker(markinterval(stickframe(n=3),true))); markangle(n=1,exX,Z,Y,radius=20,marker(markinterval(stickframe(n=3),true))); markangle(n=1,3*(Y-Z)+Z,Y,exZ,radius=22,marker(markinterval(stickframe(n=2),true))); markangle(n=1,exZ,Y,X,radius=20,marker(markinterval(stickframe(n=2),true))); markangle(n=1,3*(X-Y)+Y,X,exY,radius=22,marker(markinterval(stickframe(n=1),true))); markangle(n=1,exY,X,Z,radius=20,marker(markinterval(stickframe(n=1),true))); markangle(n=3,I,Z,X,radius=20); markangle(n=3,Y,Z,I,radius=22); markangle(n=2,Z,X,I,radius=20); markangle(n=2,I,X,Y,radius=22); markangle(n=1,X,Y,I,radius=22); markangle(n=1,I,Y,Z,radius=20); [/asy]](http://latex.artofproblemsolving.com/1/b/e/1be1fa15a3cd0653bc980757a6211e8f148e5daf.png)




