Stereographic projection

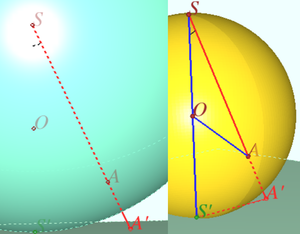
A stereographic projection is a projection from a sphere to a tangent plane. Stereographic projections preserve angles.

To stereographically project a point on a sphere to a plane tangent to its south pole, draw the line from the north pole of the sphere to the point in question. The stereographic projection of this point is then the intersection of this line with the plane. As such, the stereographic projection of the north pole will be undefined.If we completing the plane by adding a point at infinity the north pole maps to this point.

The stereographic projection of a sphere centered at $O$ with radius $R$ from its point $S$ on the set of points of this sphere coincides with the inversion of space relative to the sphere centered at $S$ with radius $2R: SA \cdot SA' = 4 R^2.$

Stereographic projection is a special case of inversion, so:

- a circle on a sphere passing through point $S$ maps into a line in the projection plane;

- a circle on a sphere not passing through point $S$ maps into a circle in the projection plane;

- angles between curves are preserved;

- tangent curves are maps into tangent ones;

- lines and circles of a plane are projected onto a sphere into circles, respectively passing and not passing through point $S.$

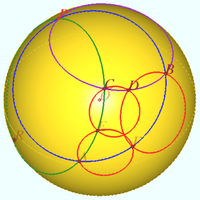
Three circles on the sphere

Three circles $PAB, PBC,$ and $PAC$ are given on a sphere. Points $D \in PAB, E \in PBC, F \in PAC,$ different from points $A, B, C,$ and $P,$ are chosen on these circles.

Prove that circles $AEF, BDF,$ and $CDE$ intersect at one point.

Proof

Let us consider a stereographic projection from point $P.$

With this transformation, circles $PAB, PBC,$ and $PAC$ will be transformed into lines $A'B', A'C',$ and $C'B'.$ Circles $AEF, BDF,$ and $CDE$ will be transformed into circles $A'E'F', B'D'F',$ and $C'D'E'.$

It is known that such circles intersect at one point $Q'.$

Thus, the desired intersection point is the preimage $Q$ of point $Q'.$

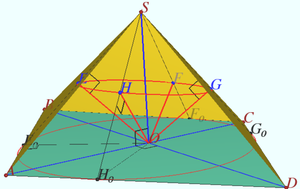
Pyramid

Let a pyramid $SABCD$ be given. Its base is a quadrilateral $ABCD, AC \perp BD.$ The altitude of a pyramid is $SO,$ where $O$ is the intersection point of the lines $AC$ and $BD.$

Prove that the bases of the perpendiculars dropped from the point $O$ to the lateral faces of the pyramid lie on one circle.

Proof

Let $E$ be the foot from $O$ to plane $ABS$ .

Let $E_0$ be the foot from $S$ to $\overline{AB}$ .

Denote $F, F_0, G, G_0, H, H_0$ similarly.

$OE_0 \perp AB, OH_0 \perp AD \implies AE_0OH_0$ is cyclic.

$\angle AOB = \angle AOD = 90^\circ \implies E_0F_0G_0H_0$ is cyclic.

$\angle SEO = 90^\circ \implies E_0$ lies on the sphere with diameter $SO,$ so point $E_0$ is a stereographic projection of point $E$ from point $S.$

Therefore $E_0F_0G_0H_0$ and $EFGH$ are cyclic simultaneously.

Moscow Math Olympiad, 1950

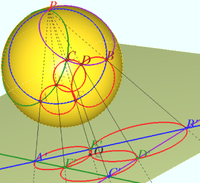
A spatial quadrilateral is circumscribed about the sphere.

Prove that the four points of contact lie in one plane.

Proof

Let given quadrilateral be $EFGH,$ the points of contact be $A,B,C,D,$ the north pole of the sphere be point $D.$ Denote sphere as $\Omega.$

Let plane $EFG$ cross sphere at circle $\omega.$ Points $D$ and $C$ lies on $\omega.$ Similarly define circles $\omega_a$ with points $A$ and $D, \omega_b$ with points $A$ and $B, \omega_c$ with points $B$ and $C.$

This circles lies in different planes and have the common points, so they are tangent in pares.

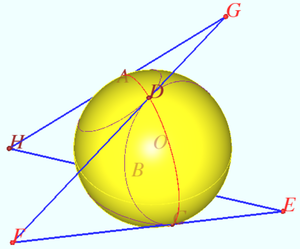
The stereographic projection from point $D$ is shown on diagram. Points $A,B,C$ maps into points $A', B', C',$ tangent circles $\omega_b$ and $\omega_c$ maps into tangent circles $\omega'_b$ and $\omega'_c,$ circles $\omega_a$ and $\omega$ maps into parallel lines $\omega'_a$ and $\omega',$ tangent to circles $\omega'_b$ and $\omega'_c,$ respectively.