Difference between revisions of "Pythagorean Theorem"
m (→Common Pythagorean Triples) |
|||
| (21 intermediate revisions by 10 users not shown) | |||
| Line 1: | Line 1: | ||
| − | The '''Pythagorean Theorem''' states that for a [[right triangle]] with | + | The '''Pythagorean Theorem''' states that for a [[right triangle]] with [[leg]]s of length <math>a</math> and <math>b</math> and [[hypotenuse]] of length <math>c</math> we have the relationship <math>a^2+b^2=c^2</math>. This theorem has been known since antiquity and is a classic to prove; hundreds of proofs have been published and many can be demonstrated entirely visually. The Pythagorean Theorem is one of the most frequently used theorems in [[geometry]], and is one of the many tools in a good geometer's arsenal. A very large number of geometry problems can be solved by building right triangles and applying the Pythagorean Theorem. |
| − | This is generalized by the [[Geometric inequality#Pythagorean_Inequality | Pythagorean Inequality]] and the [[Law of Cosines]]. | + | This is generalized by the [[Geometric inequality#Pythagorean_Inequality|Pythagorean Inequality]] and the [[Law of Cosines]]. |
== Proofs == | == Proofs == | ||
| − | In these proofs, we will let <math>ABC </math> be any right triangle with a right angle at <math> | + | In these proofs, we will let <math>ABC</math> be any right triangle with a right angle at <math>\angle ACB</math>, and we use <math>[ABC]</math> to denote the area of triangle <math>ABC</math>. |
=== Proof 1 === | === Proof 1 === | ||
| − | + | Let <math>D</math> be the foot of the [[altitude]] from <math>C</math>. <math>ABC</math>, <math>ACD</math>, <math>BCD</math> are similar triangles, so <math>\frac{AC}{AD}=\frac{AB}{AC} \implies AC^2=(AD)(AB)</math> and <math>\frac{BC}{BD}=\frac{AB}{BC} \implies BC^2=(BD)(AB)</math>. Adding these equations gives us <math>AC^2+BC^2=(AD)(AB)+(BD)(AB) \implies AC^2+BC^2=(AB)(AD+BD) \implies AC^2+BC^2=AB^2</math> | |
| − | Let <math>H </math> be the | + | === Proof 2 === |
| + | |||
| + | Let <math>H</math> be the foot of the [[altitude]] from <math>C</math>. | ||
<center> | <center> | ||
| Line 32: | Line 34: | ||
</center> | </center> | ||
| − | Since <math>ABC, CBH, ACH</math> are similar right triangles, and the areas of similar triangles are proportional to the squares of corresponding side lengths, | + | Since <math>ABC</math>, <math>CBH</math>, <math>ACH</math> are similar right triangles, and the areas of similar triangles are proportional to the squares of corresponding side lengths, |
| − | < | + | <cmath>\frac{[ABC]}{AB^2} = \frac{[CBH]}{CB^2} = \frac{[ACH]}{AC^2}.</cmath> |
| − | + | But since triangle <math>ABC</math> is composed of triangles <math>CBH</math> and <math>ACH</math>, <math>[ABC] = [CBH]+[ACH]</math>, so <math>AB^2 = CB^2 + AC^2</math>. | |
| − | </ | ||
| − | But since triangle <math>ABC </math> is composed of triangles <math>CBH </math> and <math>ACH </math>, <math>[ABC] = [CBH] + [ACH] </math>, so <math>AB^2 = CB^2 + AC^2 </math>. | ||
| − | === Proof | + | === Proof 3 === |
| − | Consider a circle <math>\omega </math> with center <math>B </math> and radius <math>BC </math>. Since <math>BC </math> and <math>AC </math> are perpendicular, <math>AC </math> is tangent to <math>\omega </math>. Let the line <math>AB </math> meet <math>\omega </math> at <math>Y </math> and <math>X </math>, as shown in the diagram: | + | Consider a circle <math>\omega</math> with center <math>B</math> and radius <math>BC</math>. Since <math>BC</math> and <math>AC</math> are perpendicular, <math>AC</math> is tangent to <math>\omega</math>. Let the line <math>AB</math> meet <math>\omega</math> at <math>Y</math> and <math>X</math>, as shown in the diagram: |
<center>[[Image:Pyth2.png]]</center> | <center>[[Image:Pyth2.png]]</center> | ||
| − | Evidently, <math>AY = AB - BC </math> and <math>AX = AB + BC </math>. By considering the [[Power of a Point | + | Evidently, <math>AY = AB-BC</math> and <math>AX = AB+BC</math>. By considering the [[Power of a Point]] <math>A</math> with respect to <math>\omega</math>, we see |
| + | <cmath>AC^2 = AY \cdot AX = (AB-BC)(AB+BC) = AB^2 - BC^2.</cmath> | ||
| − | + | === Proof 4 === | |
| − | |||
| − | |||
| − | + | Consider a square of side length \(a + b\). Inside it, place four congruent right triangles—each with legs \(a\) and \(b\) and hypotenuse \(c\)—arranged so that their right angles occupy the corners of the large square and their hypotenuses form a smaller, tilted square at the center. | |
| − | |||
| − | |||
<asy> | <asy> | ||
| − | + | unitsize(3cm); | |
| − | + | ||
| − | + | // define a and b | |
| − | + | real a = 0.6; | |
| − | + | real b = 0.8; | |
| − | pair | + | // corners of the big square |
| − | + | pair A = (0,0); | |
| − | + | pair B = (a+b, 0); | |
| − | + | pair C = (a+b, a+b); | |
| − | + | pair D = (0, a+b); | |
draw(A--B--C--D--cycle); | draw(A--B--C--D--cycle); | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | draw( | + | // four right triangles |
| − | label("$E$", | + | pair T1 = (a,0); |
| − | label("$ | + | pair T2 = (a+b, b); |
| − | label("$ | + | pair T3 = (b, a+b); |
| − | label("$ | + | pair T4 = (0, a); |
| + | |||
| + | draw(A--T1--T4--cycle); // bottom-left triangle | ||
| + | draw(T1--B--T2--cycle); // bottom-right triangle | ||
| + | draw(T4--T3--D--cycle); // top-left triangle | ||
| + | draw(T2--C--T3--cycle); // top-right triangle | ||
| + | |||
| + | // inner square formed by hypotenuses | ||
| + | draw(T1--T2--T3--T4--cycle); | ||
| + | |||
| + | // labels | ||
| + | label("$a+b$", midpoint(A--B), S); | ||
| + | label("$a+b$", midpoint(B--C), E); | ||
| + | |||
| + | label("$a$", midpoint(A--T1), S); | ||
| + | label("$b$", midpoint(T1--B), S); | ||
| + | label("$b$", midpoint(D--T4), W); | ||
| + | label("$a$", midpoint(T4--A), W); | ||
| − | label(" | + | label("$c$", midpoint(T1--T2), NE); |
| − | + | label("$c$", midpoint(T2--T3), NE); | |
| − | + | label("$c$", midpoint(T3--T4), NW); | |
| − | label(" | + | label("$c$", midpoint(T4--T1), NW); |
| − | |||
| − | |||
| − | label(" | ||
| − | |||
| − | |||
| − | label("c", | ||
| − | |||
| − | |||
</asy> | </asy> | ||
| − | |||
| − | |||
| − | == | + | The area of the large square is \((a + b)^2 = a^2 + 2ab + b^2\). The area can also be expressed as the sum of the four triangles, each with area \(\frac{1}{2}ab\), totaling \(2ab\), plus the inner square with area \(c^2\). Setting these equal gives: |
| − | A [[Pythagorean | + | <cmath> |
| + | (a + b)^2 = 4 \times \frac{1}{2} ab + c^2 = 2ab + c^2. | ||
| + | </cmath> | ||
| + | Simplifying, | ||
| + | <cmath> | ||
| + | a^2 + 2ab + b^2 = 2ab + c^2 \implies a^2 + b^2 = c^2. | ||
| + | \qquad\blacksquare | ||
| + | </cmath> | ||
| + | |||
| + | === Proof 5 (Linear Algebra / Inner Product Space) === | ||
| + | |||
| + | Consider the right triangle <math>\triangle ABC</math> with a right angle at <math>C</math>. Represent the vectors | ||
| + | <cmath> | ||
| + | \vec{AC} = \mathbf{u} \quad \text{and} \quad \vec{BC} = \mathbf{v} | ||
| + | </cmath> | ||
| + | in an inner product space equipped with the dot product <math>\langle \cdot, \cdot \rangle</math>. | ||
| + | |||
| + | Because <math>\angle ACB</math> is a right angle, the vectors <math>\mathbf{u}</math> and <math>\mathbf{v}</math> are orthogonal: | ||
| + | <cmath> | ||
| + | \langle \mathbf{u}, \mathbf{v} \rangle = 0. | ||
| + | </cmath> | ||
| + | |||
| + | By definition of the norm induced by the inner product, | ||
| + | <cmath> | ||
| + | \|\mathbf{u}\| = a, \quad \|\mathbf{v}\| = b, | ||
| + | </cmath> | ||
| + | and the hypotenuse vector is | ||
| + | <cmath> | ||
| + | \vec{AB} = \mathbf{u} - \mathbf{v}. | ||
| + | </cmath> | ||
| + | |||
| + | Calculate the squared length of <math>\vec{AB}</math>: | ||
| + | <cmath> | ||
| + | \|\vec{AB}\|^2 = \langle \mathbf{u} - \mathbf{v}, \mathbf{u} - \mathbf{v} \rangle = \langle \mathbf{u}, \mathbf{u} \rangle - 2 \langle \mathbf{u}, \mathbf{v} \rangle + \langle \mathbf{v}, \mathbf{v} \rangle. | ||
| + | </cmath> | ||
| + | |||
| + | Using orthogonality <math>\langle \mathbf{u}, \mathbf{v} \rangle = 0</math>, this reduces to | ||
| + | <cmath> | ||
| + | \|\vec{AB}\|^2 = \|\mathbf{u}\|^2 + \|\mathbf{v}\|^2 = a^2 + b^2. | ||
| + | </cmath> | ||
| + | |||
| + | Since <math>\|\vec{AB}\| = c</math>, the length of the hypotenuse, we conclude | ||
| + | <cmath> | ||
| + | c^2 = a^2 + b^2, | ||
| + | </cmath> | ||
| + | which is the Pythagorean Theorem. | ||
| + | |||
| + | This proof is highly abstract and depends on familiarity with vector spaces and inner products, moving far beyond the classical Euclidean framework into the realm of modern algebraic geometry. | ||
| + | |||
| + | == Pythagorean Triples == | ||
| + | |||
| + | {{main|Pythagorean triple}} | ||
| + | A [[Pythagorean triple]] is a of [[positive integer]]s such that <math>a^{2}+b^{2}=c^{2}</math>. All such triples contain numbers which are side lengths of the sides of a right triangle. Among these, the [[Primitive Pythagorean triple]]s, are those in which the three numbers are [[coprime]]. A few of them are: | ||
<cmath>3-4-5</cmath> | <cmath>3-4-5</cmath> | ||
| Line 107: | Line 159: | ||
<cmath>11-60-61</cmath> | <cmath>11-60-61</cmath> | ||
| + | Note that (3,4,5) is the only Pythagorean triple that consists of consecutive integers. | ||
| − | + | Any triple created by multiplying all three numbers in a Pythagorean triple by a positive integer is Pythagorean. In other words, if (a,b,c) is a Pythagorean triple it follows that (ka,kb,kc) will also form a Pythagorean triple for any positive integer constant k. | |
For example, | For example, | ||
<cmath>6-8-10 = (3-4-5)*2</cmath> | <cmath>6-8-10 = (3-4-5)*2</cmath> | ||
<cmath>21-72-75 = (7-24-25)*3</cmath> | <cmath>21-72-75 = (7-24-25)*3</cmath> | ||
<cmath>10-24-26 = (5-12-13)*2</cmath> | <cmath>10-24-26 = (5-12-13)*2</cmath> | ||
| − | |||
| − | Also | + | Also note that one easy way to find Pythagorean triples is as follows. Choose any odd number <math>n</math>. Find <math>n^2</math>. Find <math>\frac{n-1}{2}</math> and <math>\frac{n-1}{2} + 1</math>. Your Pythagorean triple is <math>n</math>, <math>\frac{n-1}{2}</math>, and <math>\frac{n-1}{2} + 1</math>. |
| − | + | == Problems == | |
| − | |||
=== Introductory === | === Introductory === | ||
| + | * [[2020 AMC 8 Problems/Problem 18 | 2020 AMC 8 Problem 18]] | ||
| + | * [[2023 AMC 10A Problems/Problem 11 | 2023 AMC 10A Problem 11]] | ||
| + | * [[2007 AMC 12A Problems/Problem 10 | 2007 AMC 12A Problem 10]] | ||
* [[2006_AIME_I_Problems/Problem_1 | 2006 AIME I Problem 1]] | * [[2006_AIME_I_Problems/Problem_1 | 2006 AIME I Problem 1]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | ==== [[2020 AMC 8 Problems/Problem 18 | Problem 1]] ==== |
| − | + | Rectangle <math>ABCD</math> is inscribed in a semicircle with diameter <math>\overline{FE},</math> as shown in the figure. Let <math>DA=16,</math> and let <math>FD=AE=9.</math> What is the area of <math>ABCD?</math> | |
| − | ==== | + | |
| − | + | <asy> | |
| − | + | draw(arc((0,0),17,180,0)); draw((-17,0)--(17,0)); fill((-8,0)--(-8,15)--(8,15)--(8,0)--cycle, 1.5*grey); draw((-8,0)--(-8,15)--(8,15)--(8,0)--cycle); dot("$A$",(8,0), 1.25*S); dot("$B$",(8,15), 1.25*N); dot("$C$",(-8,15), 1.25*N); dot("$D$",(-8,0), 1.25*S); dot("$E$",(17,0), 1.25*S); dot("$F$",(-17,0), 1.25*S); label("$16$",(0,0),N); label("$9$",(12.5,0),N); label("$9$",(-12.5,0),N); | |
| − | + | </asy> | |
| − | + | ||
| + | <math>\textbf{(A) }240 \qquad \textbf{(B) }248 \qquad \textbf{(C) }256 \qquad \textbf{(D) }264 \qquad \textbf{(E) }272</math> | ||
| + | |||
| + | [[2020_AMC_8_Problems/Problem_18 | Solution]] | ||
| + | |||
| + | ==== [[2023 AMC 10A Problems/Problem 11 | Problem 2]] ==== | ||
| + | A rhombic dodecahedron is a solid with <math>12</math> congruent rhombus faces. At every vertex, <math>3</math> or <math>4</math> edges meet, depending on the vertex. How many vertices have exactly <math>3</math> edges meet? | ||
| + | |||
| + | <math>\textbf{(A) }5\qquad\textbf{(B) }6\qquad\textbf{(C) }7\qquad\textbf{(D) }8\qquad\textbf{(E) }9</math> | ||
| − | + | [[2023_AMC_10A_Problems/Problem_18 | Solution]] | |
| − | |||
| − | [[ | + | == External Links == |
| + | * [//en.wikipedia.org/wiki/Pythagorean_theorem Wikipedia: Pythagorean Theorem] | ||
| + | * [//www.cut-the-knot.org/pythagoras/index.shtml Cut-the-Knot: 122 Proofs of the Pythagorean Theorem] | ||
| − | [[ | + | === Videos === |
| + | * [//www.youtube.com/watch?v=ZksDIM_MeNg Proving the Pythagorean Theorem] | ||
| + | * [//www.youtube.com/watch?v=JRMUfe0eDYA Using the Pythagorean Theorem Part 1] | ||
| + | * [//www.youtube.com/watch?v=d5C3QEpPBEc Using the Pythagorean Theorem Part 2] | ||
| + | * [//www.youtube.com/watch?v=RgUZkmhA9bw Pythagorean Triple Warning!] | ||
| + | * [//www.youtube.com/watch?v=mYXcwRAXWjA Power of Pythagorean Triples] | ||
[[Category:Geometry]] | [[Category:Geometry]] | ||
| + | [[Category:Theorems]] | ||
Latest revision as of 12:12, 20 June 2025
The Pythagorean Theorem states that for a right triangle with legs of length ![]() and
and ![]() and hypotenuse of length
and hypotenuse of length ![]() we have the relationship
we have the relationship ![]() . This theorem has been known since antiquity and is a classic to prove; hundreds of proofs have been published and many can be demonstrated entirely visually. The Pythagorean Theorem is one of the most frequently used theorems in geometry, and is one of the many tools in a good geometer's arsenal. A very large number of geometry problems can be solved by building right triangles and applying the Pythagorean Theorem.
. This theorem has been known since antiquity and is a classic to prove; hundreds of proofs have been published and many can be demonstrated entirely visually. The Pythagorean Theorem is one of the most frequently used theorems in geometry, and is one of the many tools in a good geometer's arsenal. A very large number of geometry problems can be solved by building right triangles and applying the Pythagorean Theorem.
This is generalized by the Pythagorean Inequality and the Law of Cosines.
Contents
Proofs
In these proofs, we will let ![]() be any right triangle with a right angle at
be any right triangle with a right angle at ![]() , and we use
, and we use ![]() to denote the area of triangle
to denote the area of triangle ![]() .
.
Proof 1
Let ![]() be the foot of the altitude from
be the foot of the altitude from ![]() .
. ![]() ,
, ![]() ,
, ![]() are similar triangles, so
are similar triangles, so ![]() and
and ![]() . Adding these equations gives us
. Adding these equations gives us ![]()
Proof 2
Let ![]() be the foot of the altitude from
be the foot of the altitude from ![]() .
.
![[asy] pair A, B, C, H; A = (0, 0); B = (4, 3); C = (4, 0); H = foot(C, A, B); draw(A--B--C--cycle); draw(C--H); draw(rightanglemark(A, C, B)); draw(rightanglemark(C, H, B)); label("$A$", A, SSW); label("$B$", B, ENE); label("$C$", C, SE); label("$H$", H, NNW); [/asy]](http://latex.artofproblemsolving.com/a/1/9/a19bed9f5ac971139756a395da4e29366d45fc52.png)
Since ![]() ,
, ![]() ,
, ![]() are similar right triangles, and the areas of similar triangles are proportional to the squares of corresponding side lengths,
are similar right triangles, and the areas of similar triangles are proportional to the squares of corresponding side lengths,
![]() But since triangle
But since triangle ![]() is composed of triangles
is composed of triangles ![]() and
and ![]() ,
, ![]() , so
, so ![]() .
.
Proof 3
Consider a circle ![]() with center
with center ![]() and radius
and radius ![]() . Since
. Since ![]() and
and ![]() are perpendicular,
are perpendicular, ![]() is tangent to
is tangent to ![]() . Let the line
. Let the line ![]() meet
meet ![]() at
at ![]() and
and ![]() , as shown in the diagram:
, as shown in the diagram:
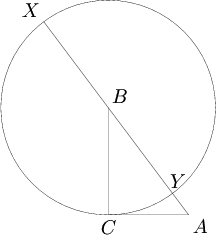
Evidently, ![]() and
and ![]() . By considering the Power of a Point
. By considering the Power of a Point ![]() with respect to
with respect to ![]() , we see
, we see
![]()
Proof 4
Consider a square of side length \(a + b\). Inside it, place four congruent right triangles—each with legs \(a\) and \(b\) and hypotenuse \(c\)—arranged so that their right angles occupy the corners of the large square and their hypotenuses form a smaller, tilted square at the center.
![[asy] unitsize(3cm); // define a and b real a = 0.6; real b = 0.8; // corners of the big square pair A = (0,0); pair B = (a+b, 0); pair C = (a+b, a+b); pair D = (0, a+b); draw(A--B--C--D--cycle); // four right triangles pair T1 = (a,0); pair T2 = (a+b, b); pair T3 = (b, a+b); pair T4 = (0, a); draw(A--T1--T4--cycle); // bottom-left triangle draw(T1--B--T2--cycle); // bottom-right triangle draw(T4--T3--D--cycle); // top-left triangle draw(T2--C--T3--cycle); // top-right triangle // inner square formed by hypotenuses draw(T1--T2--T3--T4--cycle); // labels label("$a+b$", midpoint(A--B), S); label("$a+b$", midpoint(B--C), E); label("$a$", midpoint(A--T1), S); label("$b$", midpoint(T1--B), S); label("$b$", midpoint(D--T4), W); label("$a$", midpoint(T4--A), W); label("$c$", midpoint(T1--T2), NE); label("$c$", midpoint(T2--T3), NE); label("$c$", midpoint(T3--T4), NW); label("$c$", midpoint(T4--T1), NW); [/asy]](http://latex.artofproblemsolving.com/2/a/c/2ac5d3c463113991c5cea1ee9caa6ff3a8c610e6.png)
The area of the large square is \((a + b)^2 = a^2 + 2ab + b^2\). The area can also be expressed as the sum of the four triangles, each with area \(\frac{1}{2}ab\), totaling \(2ab\), plus the inner square with area \(c^2\). Setting these equal gives:
![]() Simplifying,
Simplifying,
![]()
Proof 5 (Linear Algebra / Inner Product Space)
Consider the right triangle ![]() with a right angle at
with a right angle at ![]() . Represent the vectors
. Represent the vectors
![]() in an inner product space equipped with the dot product
in an inner product space equipped with the dot product ![]() .
.
Because ![]() is a right angle, the vectors
is a right angle, the vectors ![]() and
and ![]() are orthogonal:
are orthogonal:
![]()
By definition of the norm induced by the inner product,
![]() and the hypotenuse vector is
and the hypotenuse vector is
![]()
Calculate the squared length of ![]() :
:
![]()
Using orthogonality ![]() , this reduces to
, this reduces to
![]()
Since ![]() , the length of the hypotenuse, we conclude
, the length of the hypotenuse, we conclude
![]() which is the Pythagorean Theorem.
which is the Pythagorean Theorem.
This proof is highly abstract and depends on familiarity with vector spaces and inner products, moving far beyond the classical Euclidean framework into the realm of modern algebraic geometry.
Pythagorean Triples
- Main article: Pythagorean triple
A Pythagorean triple is a of positive integers such that ![]() . All such triples contain numbers which are side lengths of the sides of a right triangle. Among these, the Primitive Pythagorean triples, are those in which the three numbers are coprime. A few of them are:
. All such triples contain numbers which are side lengths of the sides of a right triangle. Among these, the Primitive Pythagorean triples, are those in which the three numbers are coprime. A few of them are:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Note that (3,4,5) is the only Pythagorean triple that consists of consecutive integers.
Any triple created by multiplying all three numbers in a Pythagorean triple by a positive integer is Pythagorean. In other words, if (a,b,c) is a Pythagorean triple it follows that (ka,kb,kc) will also form a Pythagorean triple for any positive integer constant k.
For example,
![]()
![]()
![]()
Also note that one easy way to find Pythagorean triples is as follows. Choose any odd number ![]() . Find
. Find ![]() . Find
. Find ![]() and
and ![]() . Your Pythagorean triple is
. Your Pythagorean triple is ![]() ,
, ![]() , and
, and ![]() .
.
Problems
Introductory
Problem 1
Rectangle ![]() is inscribed in a semicircle with diameter
is inscribed in a semicircle with diameter ![]() as shown in the figure. Let
as shown in the figure. Let ![]() and let
and let ![]() What is the area of
What is the area of ![]()
![[asy] draw(arc((0,0),17,180,0)); draw((-17,0)--(17,0)); fill((-8,0)--(-8,15)--(8,15)--(8,0)--cycle, 1.5*grey); draw((-8,0)--(-8,15)--(8,15)--(8,0)--cycle); dot("$A$",(8,0), 1.25*S); dot("$B$",(8,15), 1.25*N); dot("$C$",(-8,15), 1.25*N); dot("$D$",(-8,0), 1.25*S); dot("$E$",(17,0), 1.25*S); dot("$F$",(-17,0), 1.25*S); label("$16$",(0,0),N); label("$9$",(12.5,0),N); label("$9$",(-12.5,0),N); [/asy]](http://latex.artofproblemsolving.com/3/c/9/3c9c1a2a36307aa14183c77012405d57721363d4.png)
![]()
Problem 2
A rhombic dodecahedron is a solid with ![]() congruent rhombus faces. At every vertex,
congruent rhombus faces. At every vertex, ![]() or
or ![]() edges meet, depending on the vertex. How many vertices have exactly
edges meet, depending on the vertex. How many vertices have exactly ![]() edges meet?
edges meet?
![]()









