Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2006 AIME II Problems/Problem 1"

m (→‎Solution 2)
(Formatting)
(Tag: Undo)
 
(3 intermediate revisions by 2 users not shown)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
 +
 
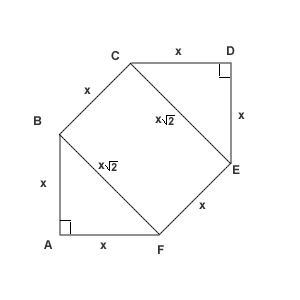
In [[convex polygon|convex]] [[hexagon]] <math>ABCDEF</math>, all six sides are congruent, <math>\angle A</math> and <math>\angle D</math> are [[right angle]]s, and <math>\angle B, \angle C, \angle E,</math> and <math>\angle F</math> are [[congruent]]. The area of the hexagonal region is <math>2116(\sqrt{2}+1).</math> Find <math>AB</math>.
 
In [[convex polygon|convex]] [[hexagon]] <math>ABCDEF</math>, all six sides are congruent, <math>\angle A</math> and <math>\angle D</math> are [[right angle]]s, and <math>\angle B, \angle C, \angle E,</math> and <math>\angle F</math> are [[congruent]]. The area of the hexagonal region is <math>2116(\sqrt{2}+1).</math> Find <math>AB</math>.
  
−
== Solution ==
+
== Solution 1 ==
 +
 
 
Let the side length be called <math>x</math>, so <math>x=AB=BC=CD=DE=EF=AF</math>.  
 
Let the side length be called <math>x</math>, so <math>x=AB=BC=CD=DE=EF=AF</math>.  
  
Line 11: Line 13:
  
 
Then we have to solve the equation  
 
Then we have to solve the equation  
−
<div style="text-align:center;">
 
−
<math>2116(\sqrt{2}+1)=x^2\sqrt{2}+x^2</math>.
 
−
 
−
<math>2116(\sqrt{2}+1)=x^2(\sqrt{2}+1)</math>
 
−
 
−
<math>2116=x^2</math>
 
  
−
<math>x=46</math></div>
+
<cmath>2116(\sqrt{2}+1)=x^2\sqrt{2}+x^2</cmath>
 +
<cmath>2116(\sqrt{2}+1)=x^2(\sqrt{2}+1)</cmath>
 +
<cmath>2116=x^2</cmath>
 +
<cmath>x=46</cmath>
  
 
Therefore, <math>AB</math> is <math>\boxed{046}</math>.
 
Therefore, <math>AB</math> is <math>\boxed{046}</math>.
Line 49: Line 48:
 
label("{\tiny $A$}",A,S);
 
label("{\tiny $A$}",A,S);
 
label("{\tiny $B$}",B,S);
 
label("{\tiny $B$}",B,S);
−
label("{\tiny $C$}",C,dir(0));
+
label("{\tiny $C$}",C,E);
 
label("{\tiny $D$}",D,N);
 
label("{\tiny $D$}",D,N);
 
label("{\tiny $E$}",E,N);
 
label("{\tiny $E$}",E,N);
Line 55: Line 54:
 
</asy>
 
</asy>
  
 +
== See Also ==
  
−
~minor asymptote edit by Yiyj1
 
−
 
−
== See also ==
 
 
{{AIME box|year=2006|n=II|before=First Question|num-a=2}}
 
{{AIME box|year=2006|n=II|before=First Question|num-a=2}}
−
 
 
[[Category:Intermediate Geometry Problems]]
 
[[Category:Intermediate Geometry Problems]]
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 18:40, 18 April 2025

Problem

In convex hexagon $ABCDEF$, all six sides are congruent, $\angle A$ and $\angle D$ are right angles, and $\angle B, \angle C, \angle E,$ and $\angle F$ are congruent. The area of the hexagonal region is $2116(\sqrt{2}+1).$ Find $AB$.

Solution 1

Let the side length be called $x$, so $x=AB=BC=CD=DE=EF=AF$.

2006 II AIME-1.png

The diagonal $BF=\sqrt{AB^2+AF^2}=\sqrt{x^2+x^2}=x\sqrt{2}$. Then the areas of the triangles AFB and CDE in total are $\frac{x^2}{2}\cdot 2$, and the area of the rectangle BCEF equals $x\cdot x\sqrt{2}=x^2\sqrt{2}$

Then we have to solve the equation

\[2116(\sqrt{2}+1)=x^2\sqrt{2}+x^2\] \[2116(\sqrt{2}+1)=x^2(\sqrt{2}+1)\] \[2116=x^2\] \[x=46\]

Therefore, $AB$ is $\boxed{046}$.

Solution 2

Because $\angle B$, $\angle C$, $\angle E$, and $\angle F$ are congruent, the degree-measure of each of them is ${{720-2\cdot90}\over4}= 135$. Lines $BF$ and $CE$ divide the hexagonal region into two right triangles and a rectangle. Let $AB=x$. Then $BF=x\sqrt2$. Thus \begin{align*} 2116(\sqrt2+1)&=[ABCDEF]\\ &=2\cdot {1\over2}x^2+x\cdot x\sqrt2=x^2(1+\sqrt2), \end{align*}so $x^2=2116$, and $x=\boxed{046}$.

[asy] pair A,B,C,D,E,F; A=(0,0); B=(7,0); C=(13,6); E=(6,13); D=(13,13); F=(0,7); dot(A); dot(B); dot(C); dot(D); dot(E); dot(F); draw(A--B--C--D--E--F--cycle,linewidth(0.7)); label("{\tiny $A$}",A,S); label("{\tiny $B$}",B,S); label("{\tiny $C$}",C,E); label("{\tiny $D$}",D,N); label("{\tiny $E$}",E,N); label("{\tiny $F$}",F,W); [/asy]

See Also

2006 AIME II (Problems • Answer Key • Resources)
Preceded by
First Question 		Followed by
Problem 2
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2006_AIME_II_Problems/Problem_1&oldid=246923"