Difference between revisions of "2025 AIME II Problems/Problem 14"
m (→Solution 4 (Trigonometry)) |
(→Solution 9) |
||
| (44 intermediate revisions by 14 users not shown) | |||
| Line 1: | Line 1: | ||
| + | == Problem == | ||
Let <math>{\triangle ABC}</math> be a right triangle with <math>\angle A = 90^\circ</math> and <math>BC = 38.</math> There exist points <math>K</math> and <math>L</math> inside the triangle such<cmath>AK = AL = BK = CL = KL = 14.</cmath>The area of the quadrilateral <math>BKLC</math> can be expressed as <math>n\sqrt3</math> for some positive integer <math>n.</math> Find <math>n.</math> | Let <math>{\triangle ABC}</math> be a right triangle with <math>\angle A = 90^\circ</math> and <math>BC = 38.</math> There exist points <math>K</math> and <math>L</math> inside the triangle such<cmath>AK = AL = BK = CL = KL = 14.</cmath>The area of the quadrilateral <math>BKLC</math> can be expressed as <math>n\sqrt3</math> for some positive integer <math>n.</math> Find <math>n.</math> | ||
| − | ==Solution 1 | + | ==Solution 1== |
| + | From the given condition, we could get <math>\angle{LAK}=60^{\circ}</math> and <math>\triangle{LCA}, \triangle{BAK}</math> are isosceles. Denote <math>\angle{BAK}=\alpha, \angle{CAL}=30^{\circ}-\alpha</math>. From the isosceles condition, we have <math>\angle{BKA}=180^{\circ}-2\alpha, \angle{CLA}=120^{\circ}+2\alpha</math> | ||
| − | + | Since <math>\angle{CAB}</math> is right, then <math>AB^2+AC^2=BC^2</math>, we could use law of cosines to express <math>AC^2, AB^2, AC^2+AB^2=2\cdot 14^2(2-\cos \angle{BKA}-\angle {CLA})=2\cdot 14^2(2+\cos(2\alpha)+\cos(60^{\circ}-2\alpha))=38^2</math> | |
| − | <math> | + | |
| + | Which simplifies to <math>\cos(2\alpha)+\cos(60^{\circ}-2\alpha)=\frac{165}{98}</math>, expand the expression by angle subtraction formula, we could get <math>\sqrt{3}\sin(2\alpha+60^{\circ})=\frac{165}{98}, \sin(2\alpha+60^{\circ})=\frac{55\sqrt{3}}{98}</math> | ||
| + | |||
| + | Conenct <math>CK</math> we could notice <math>\angle{CLK}=360^{\circ}-\angle{CLA}-\angle{ALK}=180^{\circ}-2\alpha=\angle{AKB}</math>, since <math>CL=LK=AK=KB</math> we have <math>\triangle{CLK}\cong \triangle{AKB}</math>. Moreover, since <math>K</math> lies on the perpendicular bisector of <math>AB</math>, the distance from <math>K</math> to <math>AC</math> is half of the length of <math>AB</math>, which means <math>[ACK]=\frac{[ABC]}{2}</math>, and we could have <math>[ACK]=[ACL]+[ALK]+[ABK]=[ABC]-[BKLC]</math>, so <math>[BKLC]=[AKC]</math>. We have <math>[AKC]=[ALK]+\frac{14^2}{2}(\sin(60-2\alpha)+\sin 2\alpha)=98(\sin(60+2\alpha))+[ALK]=55\sqrt{3}+\frac{\sqrt{3}}{4}14^2=104\sqrt{3}</math>, so our answer is <math>\boxed{104}</math> | ||
| − | ~ | + | ~ Bluesoul |
==Solution 2== | ==Solution 2== | ||
| Line 15: | Line 20: | ||
label("A",A,SW); label("B",B,NW); label("C",C,SE); label("A'",D,NE); label("K",K,W); label("L",L,NW); label("L'",G,SE); label("K'",F,E); label("O",O,NNW); | label("A",A,SW); label("B",B,NW); label("C",C,SE); label("A'",D,NE); label("K",K,W); label("L",L,NW); label("L'",G,SE); label("K'",F,E); label("O",O,NNW); | ||
</asy> | </asy> | ||
| − | Let <math>O</math> be the midpoint of <math>BC</math>. Take the diagram and rotate it <math>180^{\circ}</math> around <math>O</math> to get the diagram shown. Notice that we have <math>\angle ABC+\angle ACB=90^{\circ}</math>. Because <math>\triangle AKL</math> is equilateral, then <math>\angle KAL=60^{\circ}</math>, so <math>\angle BAK+\angle CAL=30^{\circ}</math>. Because of isosceles triangles <math>\triangle BAK</math> and <math>\triangle CAL</math>, we get that <math>\angle ABK+\angle ACL=30^{\circ}</math> too, implying that <math>\angle KBC+\angle LCB=60^{\circ}</math>. But by our rotation, we have <math>\angle LCO=\angle L'BO</math>, so this implies that <math>\angle KBL'=60^{\circ}</math>, or that <math>\triangle KBL'</math> is equilateral. We can similarly derive that <math>\angle KBO=\angle K'CO</math> implies <math>\angle LCK'=60^{\circ}</math> so that <math>\triangle LK' | + | Let <math>O</math> be the midpoint of <math>BC</math>. Take the diagram and rotate it <math>180^{\circ}</math> around <math>O</math> to get the diagram shown. Notice that we have <math>\angle ABC+\angle ACB=90^{\circ}</math>. Because <math>\triangle AKL</math> is equilateral, then <math>\angle KAL=60^{\circ}</math>, so <math>\angle BAK+\angle CAL=30^{\circ}</math>. Because of isosceles triangles <math>\triangle BAK</math> and <math>\triangle CAL</math>, we get that <math>\angle ABK+\angle ACL=30^{\circ}</math> too, implying that <math>\angle KBC+\angle LCB=60^{\circ}</math>. But by our rotation, we have <math>\angle LCO=\angle L'BO</math>, so this implies that <math>\angle KBL'=60^{\circ}</math>, or that <math>\triangle KBL'</math> is equilateral. We can similarly derive that <math>\angle KBO=\angle K'CO</math> implies <math>\angle LCK'=60^{\circ}</math> so that <math>\triangle LK'C</math> is also equilateral. At this point, notice that quadrilateral <math>KL'K'L</math> is a rhombus. The area of our desired region is now <math>[BKLC]=\frac{1}{2}[BL'K'CLK]</math>. We can easily find the areas of <math>\triangle KBL'</math> and <math>\triangle LK'C</math> to be <math>\frac{\sqrt{3}}{4}\cdot 14^2=49\sqrt{3}</math>. Now it remains to find the area of rhombus <math>KL'K'L</math>. |
<asy> | <asy> | ||
import math; import geometry; import olympiad; | import math; import geometry; import olympiad; | ||
| Line 28: | Line 33: | ||
~ethanzhang1001 | ~ethanzhang1001 | ||
| − | ==Solution 3== | + | ==Solution 3 (coordinates and bashy algebra)== |
| + | |||
| + | By drawing out the triangle, I set <math>A</math> to be <math>(0, 0)</math> in the coordinate plane. I set <math>C</math> to be <math>(x, 0)</math> and B to be <math>(0, y)</math>. I set <math>K</math> to be <math>(a, b)</math> and <math>L</math> to be <math>(c, d)</math>. Then, since all of these distances are <math>14</math>, I used coordinate geometry to set up the following equations: | ||
| + | <math>a^{2} + b^{2} = 196</math>; <math>a^{2} + (b - y)^{2} = 196</math>; <math>(a - c)^{2} + (b - d)^{2} = 196</math>; <math>c^{2} + d^{2} = 196</math>; <math>(c - x)^{2} + d^{2} = 196</math>. Notice by merging the first two equations, the only possible way for it to work is if <math>b - y = -b</math> which means <math>y = 2b</math>. Next, since the triangle is right, and we know one leg is <math>2b</math> as <math>y = 2b</math>, the other leg, <math>x</math>, is <math>\sqrt{38^{2} - (2b)^{2}}</math>. | ||
| + | We now have: | ||
| + | |||
| + | <math>a^{2} + b^{2} = 196 \hspace{1 cm} \textbf{(1)}</math> | ||
| + | |||
| + | <math>(a - c)^{2} + (b - d)^{2} = 196 \hspace{1 cm} \textbf{(2)}</math> | ||
| − | + | <math>c^{2} + d^{2} = 196 \hspace{1 cm} \textbf{(3)}</math> | |
| − | + | <math>(c - \sqrt{38^{2} - (2b)^{2}})^{2} + d^{2} = 196 \hspace{1 cm} \textbf{(4)}</math> | |
| − | + | Expanding equation (4) and simplifying, we end with <math>38^{2} - 4b^{2} = 2c \cdot \sqrt{38^{2} - 4b^{2}}</math>. Next, squaring both sides and canceling terms, we have <math>4 \cdot 19^{2} - 4b^{2} = 4c^{2}</math> which tells us that <math>c^{2} = 19^{2} - b^{2}</math>. Now, plugging this value in into equation (3) tells us that <math>d^{2} = 196 - 19^{2} + b^{2}</math>. We expand equation (2) to get <math>a^{2} - 2ac + c^{2} + b^{2} - 2bd + d^{2} = 196</math>. Using equation (1), we can cancel terms and shift things over to get <math>196 = 2ac + 2bd</math> which means <math>98 = ac + bd</math>. From equation (1), we have <math>a^{2} = 196 - b^{2}</math>. Now, plugging in all of our variables in terms of <math>b</math> to this new equation, we have <math>98 = \sqrt{(361 - b^{2})(196 - b^{2}} + b\sqrt{b^{2} - 165}</math>. We now move things over to get <math>98 - b\sqrt{b^{2} - 165} = \sqrt{(361 - b^{2})(196 - b^{2}}</math>. Squaring both sides and canceling, we have <math>98^{2} - 196b\sqrt{b^{2} - 165} = (361)(196) - 392b^{2}</math>. We can now divide both sides by <math>196</math> to get <math>49 - b\sqrt{b^{2} - 165} = 361 - 2b^{2}</math>. Rearranging and simplifying, we now have <math>2b^{2} - 312 = b\sqrt{b^{2} - 165}</math>. Squaring both sides and combining like terms, we have <math>3b^{4} - 1083b^{2} + 312^{2} = 0</math>. This part will be a bit of a bash. Quadratic Formula tells us that <math>b^{2} = \frac{1083 \pm \sqrt{1083^{2} - 12 \cdot 312^{2}}}{6}</math>. The discriminant nicely simplifies to <math>\sqrt{4761} = 69</math>(this will be an extremely long bash but it's worth it). In fact, after computing, we end up with <math>b^{2} = 192, 169</math>. This leads us to solutions of <math>b = 8\sqrt{3}, 13</math>. If we choose <math>b = 8\sqrt{3}</math>, then <math>c^{2} = 361 - b^{2} = 361 - 192 = 169</math> which tells us that <math>c = 13</math>.(In fact if you choose <math>b = 13</math>, then <math>c = 8\sqrt{3}</math> so it's symmetrical and doesn't matter which one you choose). Next, <math>a^{2} = 196 - b^{2} = 196 - 192 = 4</math> which tells us that <math>a = 2</math>. Finally, <math>d^{2} = 196 - c^{2} = 196 - 169 = 27</math> which tells us that <math>d = 3\sqrt{3}</math>. Therefore, after all the bashing, our solution quadruple is <math>a = 2, b = 8\sqrt{3}, c = 13, d = 3\sqrt{3}</math>. Now plugging in all the points and using the Pythagorean Theorem, we get the coordinates of the quadrilateral which are <math>(0, 16\sqrt{3}), (2, 8\sqrt{3}), (13, 3\sqrt{3})</math>, and <math>(26, 0)</math>. By Shoelace, our area is <math>104\sqrt{3}</math>. Thus, the answer is <math>\boxed{104}</math>. | |
| − | |||
| − | ~ | + | ~ilikemath247365 |
==Solution 4 (Trigonometry)== | ==Solution 4 (Trigonometry)== | ||
| Line 52: | Line 64: | ||
Immediately we should see that <math>\triangle{AKL}</math> is equilateral, so <math>\angle{KAL}=60</math>. | Immediately we should see that <math>\triangle{AKL}</math> is equilateral, so <math>\angle{KAL}=60</math>. | ||
| − | We assume <math>\angle{LCA}=x</math>, and it is easily derived that <math>\angle{KBA}=30-x</math>. Using trigonometry, we can say that <math>AC=28\cos{x}</math> and <math>AB=28\cos{30-x}</math>. Pythagoras tells us that <math>BC^2=AC^2+AB^2</math> so now we evaluate as follows: | + | We assume <math>\angle{LCA}=x</math>, and it is easily derived that <math>\angle{KBA}=30-x</math>. Using trigonometry, we can say that <math>AC=28\cos{x}</math> and <math>AB=28\cos{(30-x)}</math>. Pythagoras tells us that <math>BC^2=AC^2+AB^2</math> so now we evaluate as follows: |
\begin{align*} | \begin{align*} | ||
38^2 &=28^2(\cos^2{x}+\cos^2{(30-x)}) \ | 38^2 &=28^2(\cos^2{x}+\cos^2{(30-x)}) \ | ||
| Line 91: | Line 103: | ||
We see that <math>n=\boxed{104}</math>. | We see that <math>n=\boxed{104}</math>. | ||
| − | - | + | ~ [[User:lisztepos|lisztepos]] |
| + | |||
| + | ~ Edited by [[User:Aoum|Aoum]] | ||
| + | |||
| + | ==Solution 5 (Circles and Trigonometry)== | ||
| + | [[File:AIME2025II_P14_Solution5.PNG|450px]] | ||
| + | |||
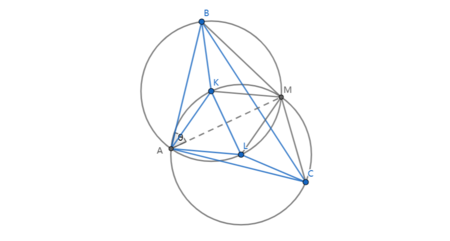
| + | Since <math>KB=KL=KA=14</math> and <math>LK=LA=LC=14</math>, we can construct 2 circles of radus 14 with <math>K</math> and <math>L</math> as the center of the two circles. Let the intersection of the 2 circles other than <math>A</math> be point <math>M</math>. Connect <math>BM</math>, <math>CM</math>, <math>KM</math>, and <math>LM</math>. Connect <math>AM</math>, which is the radical axis of the 2 circles. | ||
| + | |||
| + | From the figure, we know that | ||
| + | <cmath>[KLCB] = [KLCMB] - [BMC]</cmath> | ||
| + | <cmath>[KLCB] = [BKM] + [CLM] + [KLM] - [BMC]</cmath> | ||
| + | |||
| + | Let <math>\angle{BAM} = \theta</math>, which means that <math>\angle{CAM} = \frac{\pi}{2} - \theta</math>. For easier calculation, we temporarily define the radius of the 2 circles (which is 14) to be <math>R</math>. <math>\angle{BAM}</math> is an inscribed angle and <math>\angle{BKM}</math> is a central angle, so <math>\angle{BKM} = 2\angle{BAM} = 2\theta</math>. Similar with the other side, <math>\angle{CLM} = \pi-2\theta</math>. <math>KM = KL = LM = R</math>, so <math>\triangle{BKM}</math> is an equilateral triangle. | ||
| + | |||
| + | Using the Law of Cosines, we get the area of each little triangle. | ||
| + | <cmath>[BKM] = \frac{1}{2}\cdot R^2\cdot\sin(2\theta)</cmath> | ||
| + | <cmath>[CLM] = \frac{1}{2}\cdot R^2\cdot\sin(\pi-2\theta) = \frac{1}{2}\cdot R^2\cdot\sin(2\theta)</cmath> | ||
| + | <cmath>[KLM] = \frac{1}{2}\cdot\sin({\frac{\pi}{3}})=\frac{\sqrt3}{4}R^2</cmath> | ||
| + | \begin{align*} | ||
| + | [BMC] & = \frac{1}{2}\cdot|BM|\cdot|MC|\cdot\sin({\frac{5\pi}{6}})\ | ||
| + | &= \frac{1}{2}\cdot\frac{1}{2}\cdot2R\sin(\theta)\cdot2R\sin(\frac{\pi}{2}-\theta)\ | ||
| + | &= R^2\cdot\sin(\theta)\cos(\theta)\ | ||
| + | &= \frac{1}{2}\cdot R^2\sin(2\theta)\ | ||
| + | \end{align*} | ||
| + | |||
| + | We can conclude that | ||
| + | <cmath>[KLCB] = \frac{1}{2}\cdot R^2\cdot\sin(2\theta)+\frac{1}{2}\cdot R^2\cdot\sin(2\theta)+\frac{\sqrt3}{4}R^2-\frac{1}{2}\cdot R^2\sin(2\theta)</cmath> | ||
| + | <cmath>[KLCB] = {14}^2\cdot(\frac{\sin(2\theta)}{2}+\frac{\sqrt3}{4})</cmath> | ||
| + | |||
| + | Now, we just needed to find the value of <math>\sin(2\theta)</math>. We analyze the <math>\triangle{BMC}</math>. We already know that <math>\angle{BMC} = {150}^{\circ}</math> and <math>BM = 2R\sin(\theta)</math> and <math>BM = 2R\cos(\theta)</math>. Using the Laws of Cosines (again!) and the given condition of <math>BC = 38</math>, we can create a formula on <math>\theta</math>. | ||
| + | |||
| + | <cmath>{BC}^2 = {BM}^2+{CM}^2-2\cdot BM\cdot MC\cdot\cos(\angle{BMC})</cmath> | ||
| + | <cmath>{BC}^2 = (2R\sin(\theta))^2+(2R\cos(\theta))^2-2\cdot\cos({150}^{\circ})\cdot(2R\cos(\theta))\cdot(2R\cos(\theta)) = {38}^2</cmath> | ||
| + | <cmath>4R^2(\sin^2(\theta)+\cos^2(\theta)+\sqrt3\sin(\theta)\cos(\theta)) = {38}^2</cmath> | ||
| + | <cmath>4R^2(1+\frac{\sqrt3}{2}\cdot\sin(2\theta)) = {38}^2</cmath> | ||
| + | <cmath>4R^2+\frac{4R^2\sqrt3}{2}\cdot\sin(2\theta)) = {38}^2</cmath> | ||
| + | <cmath>\sin(2\theta) = \frac{2}{\sqrt3}\cdot(\frac{{38}^2}{4\cdot{38}^2}-1)</cmath> | ||
| + | <cmath>\sin(2\theta) = \frac{2\cdot165}{\sqrt3\cdot{14}^2} = \frac{165}{98\sqrt3}</cmath> | ||
| + | |||
| + | We put the calculated value of <math>\sin(2\theta)</math> back into <math>[KLCB]</math>: | ||
| + | <cmath>[KLCB] = {14}^2\cdot(\frac{165}{2\cdot98\sqrt3}+\frac{\sqrt3}{4})</cmath> | ||
| + | <cmath>[KLCB] = 55\sqrt3+49\sqrt3 = 104\sqrt3</cmath> | ||
| + | |||
| + | Therefore,<math>n=\boxed{104}</math>. | ||
| + | |||
| + | ~cassphe | ||
| + | |||
| + | ==Solution 6 (Trig Identities; warning: bashy)== | ||
| + | |||
| + | Consider a diagram to the original problem (credit to solution 4): | ||
| + | |||
| + | <asy> | ||
| + | import math; import geometry; import olympiad; | ||
| + | point A,B,C,L,K; A=(0,0); C=(16sqrt(3),0); B=(0,26); L=(8sqrt(3),2); K=(3sqrt(3),13); | ||
| + | draw(A--B--C--cycle); draw(A--K--L--cycle); draw(B--K); draw(C--L); draw(B--L); | ||
| + | label("A",A,SW); label("B",B,NW); label("C",C,SE); label("K",K,W); label("L",L,NE); | ||
| + | markscalefactor=1; | ||
| + | </asy> | ||
| + | |||
| + | Now, let us simplify the problem further. We know that <math>K</math> and <math>L</math> must lie on the perpendicular bisectors of <math>AB</math> and <math>AC</math>, respectively. The real problem here is the equilateral triangle in the middle, inscribed in a rectangle with diagonal length 19. | ||
| + | |||
| + | We create a further simplified problem: given that the inscribed equilateral triangle of a certain rectangle with diagonal length <math>19</math> has side length <math>14</math>, find the sides and intersection points on this rectangle. For reference, here is a diagram: | ||
| + | |||
| + | <asy> | ||
| + | import math; import geometry; import olympiad; | ||
| + | point A,B,C,D,L,K; A=(0,0); D=(13,0); B=(0,8sqrt(3)); C=(13,8sqrt(3)); L=(13,3sqrt(3)); K=(2,8sqrt(3)); | ||
| + | draw(A--B--C--D--cycle); draw(A--K--L--cycle); | ||
| + | label("A",A,SW); label("B",B,NW); label("C",C,NE); label("K",K,N); label("L",L,E); label("D",D,SE); | ||
| + | markscalefactor=1; | ||
| + | </asy> | ||
| + | |||
| + | |||
| + | |||
| + | Note the angles <math>\angle{LAD}</math> and <math>\angle{BAK}</math>. Since <math>\angle{LAD} + \angle{BAK} + 60^{\circ} = 90^{\circ}</math>, <math>\angle{LAD} + \angle{BAK} = 30^{\circ}</math>, and <math>\angle{BAK} = 30^{\circ} - \angle{LAD}</math>. Thus, let <math>\angle{LAD} = \alpha</math> and <math>\angle{BAK} = 30 - \alpha</math>. | ||
| + | |||
| + | Now, we know that <math>AB^2 + AD^2 = 19^2</math>, as the hypotenuse of the larger right triangle is <math>38</math>. However, we can also express AB and AB in terms of <math>\alpha</math>: <math>AB = 14(\cos(30^{\circ}-\alpha))</math> and <math>AD = 14(\cos(\alpha))</math>. Thus, <math>\cos^2(\alpha) + \cos^2(30^{\circ}-\alpha) = 361/196</math>. We expand this using the cosine difference identity: | ||
| + | |||
| + | <math>\cos^2(\alpha) + (\cos(30^{\circ})\cos(\alpha) + \sin(30^{\circ})\sin(\alpha))^2 = \frac{361}{196}</math> | ||
| + | |||
| + | <math>\frac{7}{4}\cos^2(\alpha) + \frac{1}{4}\sin^2(\alpha) + \frac{\sqrt3}{2}\sin(\alpha)\cos(\alpha) = \frac{361}{196}</math> | ||
| + | |||
| + | Using the fact that <math>\sin^2(\alpha) + \cos^2(\alpha) = 1</math>, then multiplying the entire equation by <math>2</math>, | ||
| + | |||
| + | <math>3\cos^2(\alpha) + \sqrt3\sin(\alpha)\cos(\alpha) = \frac{156}{49}</math> | ||
| + | |||
| + | Now, to save some writing, let us denote <math>\sin(\alpha)</math> with <math>x</math>, and <math>\cos(\alpha)</math> with <math>y</math>. | ||
| + | |||
| + | We have the following equations: | ||
| + | |||
| + | <math>x^2 + y^2 = 1</math> | ||
| + | |||
| + | <math>3y^2 + \sqrt3xy = \frac{156}{49}</math> | ||
| + | |||
| + | Substituting <math>x</math> for <math>y</math>, moving <math>3y^2</math> to the left side, squaring, and dividing by 9, we end up with the quartic: | ||
| + | |||
| + | <math>\frac{4}{3}y^4 - \frac{361}{147}y^2 + \frac{52^2}{49^2} = 0</math> | ||
| + | |||
| + | Using the quadratic formula, we end up with this: | ||
| + | |||
| + | <math>y^2 = \frac{\frac{361}{49} \pm \frac{1}{49}\cdot\sqrt{361^2 - 208^2\cdot3}}{8}</math> | ||
| + | |||
| + | Now, we could just compute <math>361^2 - 208^2\cdot3</math>, but instead, we can do this: | ||
| + | |||
| + | <math>361^2 - 208^2\cdot3 = (129600 + 720 + 1) - (40000 + 3200 + 64)\cdot3</math> | ||
| + | |||
| + | <math>(129600 + 721) - (43200 + 64)\cdot3</math> | ||
| + | |||
| + | <math>(129600 + 721) - (129600 + 192) = 529 = 23^2</math> | ||
| + | |||
| + | Thus, we have two cases: | ||
| + | |||
| + | <math>1. \cos(\alpha) = \frac{13}{14}</math> | ||
| + | |||
| + | <math>2. \cos(\alpha) = \frac{4\sqrt3}{7}</math> | ||
| + | |||
| + | Both lead to the same side lengths of the rectangle: <math>8\sqrt3</math>, and <math>13</math>. Referring back to our original rectangle diagram and plugging in our trigonometric values, we get that <math>CK = 13 - 2 = 11</math>, and <math>CL = 8\sqrt3 - 3\sqrt3 = 5\sqrt3</math>. Thus, the area of the original quadrilateral is <math>\frac{88\sqrt3 + 55\sqrt3 + 65\sqrt3}{2}</math>, or <math>\boxed{104}\sqrt3</math>. | ||
| + | |||
| + | ~Stead | ||
| + | |||
| + | ==Solution 7 (analytic geometry with roots of unity)== | ||
| + | |||
| + | <asy> | ||
| + | import math; import geometry; import olympiad; | ||
| + | point A,B,C,L,K; A=(0,0); C=(16sqrt(3),0); B=(0,26); L=(8sqrt(3),2); K=(3sqrt(3),13); | ||
| + | point M,N; M=(8sqrt(3), 0); N=(0,13); | ||
| + | draw(A--B--C--cycle); draw(A--K--L--cycle); draw(B--K); draw(C--L); | ||
| + | draw(N--K); draw(L--M); | ||
| + | label("A",A,SW); label("B",B,NW); label("C",C,SE); label("K",K,ENE); label("L",L,NE); | ||
| + | label(“N”,N,W); label(“M”,M,S); | ||
| + | point am, ml, an, nk, mc, bn; | ||
| + | am=(4sqrt(3), 0); mc=(12sqrt(3),0); ml=(8sqrt(3),1); an=(0,6.5); bn=(0,19.5); | ||
| + | nk=(2.5981, 13); | ||
| + | label(“a",am,S); label(“a",mc,S); label(“y”,ml,ESE); | ||
| + | label(“b”,an,W); label(“b”,bn,W); label(“x”,nk,S); | ||
| + | markscalefactor=1; | ||
| + | </asy> | ||
| + | This diagram is modified from the solution 4 diagram. Let <math>M</math> be the midpoint of <math>AC</math>, and let <math>N</math> be the midpoint of <math>AB</math>. | ||
| + | |||
| + | We place the diagram onto the Cartesian coordinate grid. Let <math>A = (0, 0)</math>, <math>M = (a, 0)</math>, <math>C = (2a, 0)</math>, <math>N = (0, b)</math>, and <math>B = (0, 2b)</math>. We are given <math>AL = CL</math>, so <math>\triangle ACL</math> is isosceles. Therefore, <math>LM</math> is the perpendicular bisector of <math>AC</math>, so we can let <math>L = (a, y)</math>. Similarly, we’re given <math>AK = BK</math>, so <math>\triangle ABK</math> is also isosceles, and <math>NK</math> is the perpendicular bisector of <math>AB</math>. Therefore, we can let <math>K = (x, b)</math>. | ||
| + | |||
| + | We have <math>AB = 2b</math> and <math>AC = 2a</math>. We’re given that <math>\angle BAC = 90^\circ</math> and <math>BC = 38</math>, so by the Pythagorean theorem, <cmath>(2a)^2 + (2b)^2 = 38^2 \implies 4a^2 + 4b^2 = 1444 \implies a^2 + b^2 = 361.</cmath> | ||
| + | |||
| + | We now place the diagram onto the complex plane. We use the x-axis of the coordinate plane as the complex plane’s real axis, and we use the y-axis of the coordinate plane as the complex plane’s imaginary axis. So, on the complex plane, <math>A = 0</math>, <math>L = a + yi</math>, and <math>K = x + bi</math>. Also, since we are given <math>AK = KL = AL</math>, <math>\triangle AKL</math> is equilateral. In addition, since <math>AL = AK</math>, <math>\angle KAL = 60^\circ</math>, and because we constructed our diagram with <math>K</math> counterclockwise of <math>L</math> (if it were the other way around, we could go through the same steps as this solution, but with variables switched around), <math>K</math> is a <math>60^\circ</math> counterclockwise rotation of <math>L</math> about <math>A</math>, and <math>L</math> is a <math>60^\circ</math> clockwise or <math>300^\circ</math> counterclockwise rotation of <math>K</math> about <math>A</math>. | ||
| + | |||
| + | Rotation on the complex plane is equivalent to multiplying by a root of unity. Here, <math>K</math> and <math>L</math> are rotated a multiple of <math>60^\circ</math> to each other about <math>A</math>. <math>60^\circ</math> is one-sixth of a full circle, so to go from <math>L</math> to <math>K</math> or <math>K</math> to <math>L</math>, we multiply by a 6th root of unity. Specifically, to go from <math>L</math> to <math>K</math>, we multiply by <math>\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}i</math>, and to go from <math>K</math> to <math>L</math>, we multiply by <math>\dfrac{1}{2} - \dfrac{\sqrt{3}}{2}i</math>. | ||
| + | |||
| + | We multiply the coordinate of <math>L</math> by <math>\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}i</math> on the complex plane to obtain equations for the coordinates of <math>K</math>: <cmath>(a + yi)\left(\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}i\right) = \left(\dfrac{a}{2} - \dfrac{\sqrt{3}}{2}y\right) + \left(\dfrac{y}{2} + \dfrac{\sqrt{3}}{2}a\right)i = x + bi.</cmath> Equating real and imaginary parts, we obtain <cmath>x = \dfrac{a}{2} - \dfrac{\sqrt{3}}{2}y \text{ and } b = \dfrac{y}{2} + \dfrac{\sqrt{3}}{2}a.</cmath> | ||
| + | |||
| + | Similarly, we multiply the coordinate of <math>K</math> by <math>\dfrac{1}{2} - \dfrac{\sqrt{3}}{2}i</math> to obtain equations for the coordinates of <math>L</math>: <cmath>(x + bi)\left(\dfrac{1}{2} - \dfrac{\sqrt{3}}{2}i\right) = \left(\dfrac{x}{2} + \dfrac{\sqrt{3}}{2}b\right) + \left(\dfrac{b}{2} - \dfrac{\sqrt{3}}{2}x\right) = a + yi.</cmath> Equating real and imaginary parts, we obtain <cmath>a = \dfrac{x}{2} + \dfrac{\sqrt{3}}{2}b \text{ and } y = \dfrac{b}{2} - \dfrac{\sqrt{3}}{2}x.</cmath> | ||
| + | |||
| + | We now look back at the problem to see what it asks for: <math>[BKLC]</math>. Looking at the diagram, we see we can express the area of the quadrilateral as the area of the big right triangle <math>ABC</math> minus the two isosceles triangles <math>ABK</math> and <math>ALC</math> minus the equilateral triangle <math>AKL</math>: <cmath>[BKLC] = [ABC] - [ABK] - [ACL] - [AKL].</cmath> | ||
| + | |||
| + | We are given that <math>AK = KL = AL = 14</math>, so the area of equilateral triangle <math>AKL</math> is <math>\dfrac{\sqrt{3}}{4} \cdot 14^2 = 49\sqrt{3}</math>. Also, we can use <math>AC = 2a</math> as the base of <math>\triangle ABC</math> and <math>AB = 2b</math> as the height, so <math>[ABC] = \dfrac{(2a)(2b)}{2} = 2ab</math>. Similarly, we use <math>AC = 2a</math> as the base of <math>\triangle ACL</math> and <math>ML = y</math> (<math>M = (a, 0)</math> and <math>L = (a, y)</math>, so the distance between the two is equal to <math>y</math>) as the height, so <math>[ACL] = \dfrac{(2a)(y)}{2} = ay</math>. Finally, we use <math>AB = 2b</math> and <math>KN = x</math> (<math>N = (0, b)</math> and <math>K = (x, b)</math>, so the distance between the two is equal to <math>x</math>) as the base and height of <math>\triangle ABK</math> respectively, so <math>[ABK] = \dfrac{(2b)(x)}{2} = bx</math>. Therefore, <cmath>[BKLC] = [ABC] - [ABK] - [ACL] - [AKL] = 2ab - bx - ay - 49\sqrt{3}.</cmath> | ||
| + | |||
| + | We have already shown that <math>b = \dfrac{y}{2} + \dfrac{\sqrt{3}}{2}a</math>. Substituting this into <math>a^2 + b^2 = 361</math>, we have <cmath>a^2 + \left(\dfrac{y}{2} + \dfrac{\sqrt{3}}{2}a\right)^2 = 361.</cmath> Expanding this out, we have <cmath>a^2 + \dfrac{y^2}{4} + \dfrac{\sqrt{3}}{2}ay + \dfrac{3}{4}a^2 = 361.</cmath> Multiplying both sides by <math>4</math> and rearranging the left side, we have <cmath>7a^2 + y^2 + 2ay\sqrt{3} = 1444.</cmath> We previously showed that <math>AC \perp ML</math>, so <math>AM \perp ML</math> (since <math>M</math> is on <math>AC</math>). Therefore, <math>\triangle AML</math> has a right angle at <math>M</math>. By the Pythagorean theorem, <math>AM^2 + ML^2 = a^2 + y^2 = AL^2 = 196</math>. Subtracting <math>a^2 + y^2</math> from the left side and <math>196</math> from the right side, we obtain <cmath>6a^2 + 2ay\sqrt{3} = 1248.</cmath> Dividing both sides of the equation by <math>2\sqrt{3}</math> and factoring <math>a</math> out of the left side, we have <cmath>a(a\sqrt{3} + y) = 208\sqrt{3}.</cmath> However, we have <math>b = \dfrac{y}{2} + \dfrac{\sqrt{3}}{2}a</math>, so the expression inside the parentheses is simply <math>2b</math>! Therefore, <cmath>2ab = 208\sqrt{3}.</cmath> | ||
| + | |||
| + | The algebra’s not over yet. We also showed that <math>a = \dfrac{x}{2} + \dfrac{\sqrt{3}}{2}b</math>, so substituting that into <math>a^2 + b^2 + 361</math>, we obtain <cmath>b^2 + \left(\dfrac{x}{2} + \dfrac{\sqrt{3}}{2}b\right)^2 = 361.</cmath> Expanding this out, we have <cmath>b^2 + \dfrac{x^2}{4} + \dfrac{\sqrt{3}}{2}bx + \dfrac{3}{4}b^2 = 361.</cmath> Multiplying both sides by <math>4</math> and rearranging the left side, we now have <cmath>7b^2 + x^2 + 2xb\sqrt{3} = 1444.</cmath> Does this equation look familiar? We previously showed that <math>NK \perp AB</math>. Therefore, <math>NK \perp AN</math> (since <math>N</math> is on <math>AB</math>). So, <math>\triangle ANK</math> has a right angle at <math>N</math>. By the Pythagorean theorem, <math>AN^2 + KN^2 = b^2 + x^2 = AK^2 = 196</math>. Subtracting <math>b^2 + x^2</math> from the left side and <math>196</math> from the right side, we have <cmath>6b^2 + 2xb\sqrt{3} = 1248.</cmath> We previously also had the equation <math>6a^2 + 2ay\sqrt{3} = 1248</math>, and adding this equation to the above equation and factoring out <math>2\sqrt{3}</math>, we have <cmath>6a^2 + 6b^2 + 2\sqrt{3}(bx + ay) = 2496.</cmath> We previously showed <math>a^2 + b^2 = 361</math>, so <math>6a^2 + 6b^2 = 6 \cdot 361 = 2166</math>. Subtracting <math>6a^2 + 6b^2</math> from the left side and <math>2166</math> from the right side, we obtain <math>2\sqrt{3}(bx + ay) = 330</math>. Finally, dividing both sides by <math>2\sqrt{3}</math>, we have <cmath>bx + ay = 55\sqrt{3}.</cmath> | ||
| + | |||
| + | We previously arrived at this expression for <math>[BKLC]</math>: <cmath>[BKLC] = 2ab - bx - ay - 49\sqrt{3}.</cmath> We now know <math>2ab = 208\sqrt{3}</math> and <math>bx + ay = 55\sqrt{3}</math>, so we can simply substitute them in. Therefore, <cmath>[BKLC] = 2ab - bx - ay - 49\sqrt{3} = 208\sqrt{3} - 55\sqrt{3} - 49\sqrt{3} = 104\sqrt{3}.</cmath> Finally, we are given <math>[BKLC] = n\sqrt{3}</math> for some integer <math>n</math>. We know <math>[BKLC] = 104\sqrt{3}</math>, so <math>n = \boxed{104}</math>. | ||
| + | |||
| + | Notice that <math>[BKLC] = 104\sqrt{3} = \dfrac{208\sqrt{3}}{2} = \dfrac{[ABC]}{2}</math>. Is this a coincidence? | ||
| + | |||
| + | ~V0305 | ||
| + | ==Solution 8== | ||
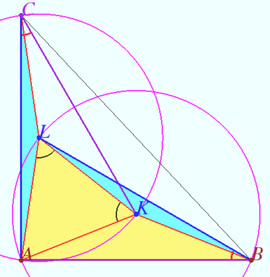
| + | [[File:2025 AIME II 14 vvsss.png|270px|right]] | ||
| + | <math>AK = BK = KL, \angle AKL = 60 ^\circ \implies \angle ABL = 30^\circ.</math> | ||
| + | |||
| + | Similarly, <math>\angle ACK = 30^\circ.</math> | ||
| + | <cmath>\angle BAK = \angle ABK, \angle LBK + \angle ABK = 30^\circ.</cmath> | ||
| + | <cmath>\angle CAL + \angle BAK = 90^\circ - \angle LAK = 30^\circ \implies</cmath> | ||
| + | <cmath>\angle CAL = \angle LBK \implies \triangle KLB = \triangle LAC \implies</cmath> | ||
| + | <math>AC = BL.</math> Similarly, <math>AB = CK.</math> | ||
| + | |||
| + | Denote the area of triangle <math>X</math> as <math>[X].</math> | ||
| + | <cmath>2[ABL] = AB \cdot BL \cdot \sin 30^\circ = \frac{AB \cdot AC}{2} = [ABC].</cmath> | ||
| + | Similarly, <math>[ABL] = [ACK] = \frac {[ABC]}{2}.</math> | ||
| + | <cmath>[BKLC] = [ABC] - [ABL] - [ALC]+ [BLK] = [ABC] - [ABL] = [ABL].</cmath> | ||
| + | By applying the Law of Cosines on <math>\triangle ABL,</math> we get | ||
| + | <math>AB^2 + BL^2 - 2 AB \cdot BL \cos 30^\circ = AL^2 \implies AB^2 + AC^2 - AB \cdot AC \sqrt{3} = AL^2 \implies</math> | ||
| + | <cmath>BC^2 - AL^2 = 4 [BKLC] \sqrt{3} \implies</cmath> | ||
| + | <cmath>[BLKC] = \frac {38^2-14^2}{4 \sqrt{3}} = \frac{19^2-7^2}{3} \sqrt{3} = 4 \cdot 26 \sqrt{3} = 104 \sqrt{3}.</cmath> | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | ==Solution 9== | ||
| + | |||
| + | <math>\triangle KAL</math> is clearly equilateral, and <math>\triangle AKB</math> and <math>\triangle ALC</math> are clearly isosceles. Now, we can do a bit of angle chasing. Say <math>\angle AKB = 2\theta</math>. Then, since <math>\triangle AKB</math> is isosceles, <math>\angle ABK = 90 - \theta</math>. <math>\angle KAL = 60^\circ</math>, so <math>\angle LAC = \theta - 60</math>, so <math>\angle ALC = 300 - 2\theta</math>, so <math>\angle KLC = 2\theta</math>. Since the angles are congruent, <math>\triangle AKB</math> is congruent to <math>\triangle KLC</math>. As such, we can rotate it around the center of <math>\triangle KAL</math> onto side AL to produce <math>\triangle LAD</math>. Because all the triangles are congruent, connecting the congruent corners will all produce the same length. From BC, we see that this length is <math>38</math>, so <math>\triangle BCD</math> is equilateral with side length <math>38</math>. This triangle is comprised of 3 quadrilaterals and <math>\triangle KAL</math> in the center, and it's easy to see that each quadrilateral is congruent to <math>BKLC</math>. As such, <math>[BKLC] = \frac{[BCD]-[KAL]}{3} = \frac{361 \sqrt{3} - 49 \sqrt{3}}{3} = 104 \sqrt{3}</math>, giving an answer of <math>\boxed{104}</math>. | ||
| + | |||
| + | ~noob1877 | ||
| + | |||
| + | ==Video Solution (Angle chasing and congruent triangles)== | ||
| + | https://youtu.be/APaVy8OqJ04?si=MSBv1fS1ajjqcxN6 | ||
==Remarks== | ==Remarks== | ||
Latest revision as of 18:33, 8 July 2025
Contents
[hide]- 1 Problem
- 2 Solution 1
- 3 Solution 2
- 4 Solution 3 (coordinates and bashy algebra)
- 5 Solution 4 (Trigonometry)
- 6 Solution 5 (Circles and Trigonometry)
- 7 Solution 6 (Trig Identities; warning: bashy)
- 8 Solution 7 (analytic geometry with roots of unity)
- 9 Solution 8
- 10 Solution 9
- 11 Video Solution (Angle chasing and congruent triangles)
- 12 Remarks
- 13 See also
Problem
Let ![]() be a right triangle with
be a right triangle with ![]() and
and ![]() There exist points
There exist points ![]() and
and ![]() inside the triangle such
inside the triangle such![]() The area of the quadrilateral
The area of the quadrilateral ![]() can be expressed as
can be expressed as ![]() for some positive integer
for some positive integer ![]() Find
Find ![]()
Solution 1
From the given condition, we could get ![]() and
and ![]() are isosceles. Denote
are isosceles. Denote ![]() . From the isosceles condition, we have
. From the isosceles condition, we have ![]()
Since ![]() is right, then
is right, then ![]() , we could use law of cosines to express
, we could use law of cosines to express ![]()
Which simplifies to ![]() , expand the expression by angle subtraction formula, we could get
, expand the expression by angle subtraction formula, we could get ![]()
Conenct ![]() we could notice
we could notice ![]() , since
, since ![]() we have
we have ![]() . Moreover, since
. Moreover, since ![]() lies on the perpendicular bisector of
lies on the perpendicular bisector of ![]() , the distance from
, the distance from ![]() to
to ![]() is half of the length of
is half of the length of ![]() , which means
, which means ![]() , and we could have
, and we could have ![]() , so
, so ![]() . We have
. We have ![]() , so our answer is
, so our answer is ![]()
~ Bluesoul
Solution 2
![[asy] import math; import geometry; import olympiad; point A,C,B,L,K,D,F,G,O; A=(0,0); C=(16sqrt(3),0); B=(0,26); L=(8sqrt(3),2); K=(3sqrt(3),13); D=(16sqrt(3),26); F=(13sqrt(3),13); G=(8sqrt(3),24); O=(8sqrt(3),13); draw(A--B--D--C--A--L--C--F--L--K--A--D); draw(K--B--G--D--F--G--K--F); draw(B--O--L); draw(C--O--G); label("A",A,SW); label("B",B,NW); label("C",C,SE); label("A'",D,NE); label("K",K,W); label("L",L,NW); label("L'",G,SE); label("K'",F,E); label("O",O,NNW); [/asy]](http://latex.artofproblemsolving.com/4/c/5/4c5cf840df95d9da69b20f4e91f0b3182dcc0b2b.png) Let
Let ![]() be the midpoint of
be the midpoint of ![]() . Take the diagram and rotate it
. Take the diagram and rotate it ![]() around
around ![]() to get the diagram shown. Notice that we have
to get the diagram shown. Notice that we have ![]() . Because
. Because ![]() is equilateral, then
is equilateral, then ![]() , so
, so ![]() . Because of isosceles triangles
. Because of isosceles triangles ![]() and
and ![]() , we get that
, we get that ![]() too, implying that
too, implying that ![]() . But by our rotation, we have
. But by our rotation, we have ![]() , so this implies that
, so this implies that ![]() , or that
, or that ![]() is equilateral. We can similarly derive that
is equilateral. We can similarly derive that ![]() implies
implies ![]() so that
so that ![]() is also equilateral. At this point, notice that quadrilateral
is also equilateral. At this point, notice that quadrilateral ![]() is a rhombus. The area of our desired region is now
is a rhombus. The area of our desired region is now ![]() . We can easily find the areas of
. We can easily find the areas of ![]() and
and ![]() to be
to be ![]() . Now it remains to find the area of rhombus
. Now it remains to find the area of rhombus ![]() .
.
![[asy] import math; import geometry; import olympiad; point A,K,O,L,M; A=(-7sqrt(3),0); K=(0,7); O=(55sqrt(3)/14,23/14); L=(0,-7); M=(0,0); draw(A--K--O--L--A--O--M--A); draw(K--L); label("A",A,W); label("K",K,N); label("O",O,E); label("L",L,S); label("M",M,SE); [/asy]](http://latex.artofproblemsolving.com/3/e/3/3e3b78d7ea0adac827ae7cf21f7d100bea89c580.png) Focus on the quadrilateral
Focus on the quadrilateral ![]() . Restate the configuration in another way - we have equilateral triangle
. Restate the configuration in another way - we have equilateral triangle ![]() with side length 14, and a point
with side length 14, and a point ![]() such that
such that ![]() and
and ![]() . We are trying to find the area of
. We are trying to find the area of ![]() . Let
. Let ![]() be the midpoint of
be the midpoint of ![]() . We see that
. We see that ![]() , and since
, and since ![]() is the circumcenter of
is the circumcenter of ![]() , it follows that
, it follows that ![]() . Let
. Let ![]() . From the Law of Cosines in
. From the Law of Cosines in ![]() , we can see that
, we can see that ![]() so after simplification we get that
so after simplification we get that ![]() . Then by trigonometric identities this simplifies to
. Then by trigonometric identities this simplifies to ![]() . Applying the definition
. Applying the definition ![]() gives us that
gives us that ![]() . Applying the Law of Cosines again in
. Applying the Law of Cosines again in ![]() , we get that
, we get that ![]() which tells us that
which tells us that ![]() . The Pythagorean Theorem in
. The Pythagorean Theorem in ![]() gives that
gives that ![]() , so the area of
, so the area of ![]() is
is ![]() . The rhombus
. The rhombus ![]() consists of four of these triangles, so its area is
consists of four of these triangles, so its area is ![]() .
.
Finally, the area of hexagon ![]() is
is ![]() , and since this consists of quadrilaterals
, and since this consists of quadrilaterals ![]() and
and ![]() which must be congruent by that rotation, the area of
which must be congruent by that rotation, the area of ![]() is
is ![]() . Therefore the answer is
. Therefore the answer is ![]() .
.
~ethanzhang1001
Solution 3 (coordinates and bashy algebra)
By drawing out the triangle, I set ![]() to be
to be ![]() in the coordinate plane. I set
in the coordinate plane. I set ![]() to be
to be ![]() and B to be
and B to be ![]() . I set
. I set ![]() to be
to be ![]() and
and ![]() to be
to be ![]() . Then, since all of these distances are
. Then, since all of these distances are ![]() , I used coordinate geometry to set up the following equations:
, I used coordinate geometry to set up the following equations:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Notice by merging the first two equations, the only possible way for it to work is if
. Notice by merging the first two equations, the only possible way for it to work is if ![]() which means
which means ![]() . Next, since the triangle is right, and we know one leg is
. Next, since the triangle is right, and we know one leg is ![]() as
as ![]() , the other leg,
, the other leg, ![]() , is
, is ![]() .
We now have:
.
We now have:
![]()
![]()
![]()
![]()
Expanding equation (4) and simplifying, we end with ![]() . Next, squaring both sides and canceling terms, we have
. Next, squaring both sides and canceling terms, we have ![]() which tells us that
which tells us that ![]() . Now, plugging this value in into equation (3) tells us that
. Now, plugging this value in into equation (3) tells us that ![]() . We expand equation (2) to get
. We expand equation (2) to get ![]() . Using equation (1), we can cancel terms and shift things over to get
. Using equation (1), we can cancel terms and shift things over to get ![]() which means
which means ![]() . From equation (1), we have
. From equation (1), we have ![]() . Now, plugging in all of our variables in terms of
. Now, plugging in all of our variables in terms of ![]() to this new equation, we have
to this new equation, we have ![]() . We now move things over to get
. We now move things over to get ![]() . Squaring both sides and canceling, we have
. Squaring both sides and canceling, we have ![]() . We can now divide both sides by
. We can now divide both sides by ![]() to get
to get ![]() . Rearranging and simplifying, we now have
. Rearranging and simplifying, we now have ![]() . Squaring both sides and combining like terms, we have
. Squaring both sides and combining like terms, we have ![]() . This part will be a bit of a bash. Quadratic Formula tells us that
. This part will be a bit of a bash. Quadratic Formula tells us that ![]() . The discriminant nicely simplifies to
. The discriminant nicely simplifies to ![]() (this will be an extremely long bash but it's worth it). In fact, after computing, we end up with
(this will be an extremely long bash but it's worth it). In fact, after computing, we end up with ![]() . This leads us to solutions of
. This leads us to solutions of ![]() . If we choose
. If we choose ![]() , then
, then ![]() which tells us that
which tells us that ![]() .(In fact if you choose
.(In fact if you choose ![]() , then
, then ![]() so it's symmetrical and doesn't matter which one you choose). Next,
so it's symmetrical and doesn't matter which one you choose). Next, ![]() which tells us that
which tells us that ![]() . Finally,
. Finally, ![]() which tells us that
which tells us that ![]() . Therefore, after all the bashing, our solution quadruple is
. Therefore, after all the bashing, our solution quadruple is ![]() . Now plugging in all the points and using the Pythagorean Theorem, we get the coordinates of the quadrilateral which are
. Now plugging in all the points and using the Pythagorean Theorem, we get the coordinates of the quadrilateral which are ![]() , and
, and ![]() . By Shoelace, our area is
. By Shoelace, our area is ![]() . Thus, the answer is
. Thus, the answer is ![]() .
.
~ilikemath247365
Solution 4 (Trigonometry)
![[asy] import math; import geometry; import olympiad; point A,B,C,L,K; A=(0,0); C=(16sqrt(3),0); B=(0,26); L=(8sqrt(3),2); K=(3sqrt(3),13); draw(A--B--C--cycle); draw(A--K--L--cycle); draw(B--K); draw(C--L); draw(B--L); label("A",A,SW); label("B",B,NW); label("C",C,SE); label("K",K,W); label("L",L,NE); markscalefactor=1; draw(anglemark(L,C,A)); draw(anglemark(A,B,K)); [/asy]](http://latex.artofproblemsolving.com/7/b/a/7baf2caf69ba181c0943335a9233e0c386636992.png) Immediately we should see that
Immediately we should see that ![]() is equilateral, so
is equilateral, so ![]() .
.
We assume ![]() , and it is easily derived that
, and it is easily derived that ![]() . Using trigonometry, we can say that
. Using trigonometry, we can say that ![]() and
and ![]() . Pythagoras tells us that
. Pythagoras tells us that ![]() so now we evaluate as follows:
so now we evaluate as follows:
It is obvious that ![]() . We can easily derive
. We can easily derive ![]() using angle addition we know, and then using cosine rule to find side
using angle addition we know, and then using cosine rule to find side ![]() .
.
We easily find ![]() and
and ![]() (draw a perpendicular down from
(draw a perpendicular down from ![]() to
to ![]() ). What we are trying to find is the area of
). What we are trying to find is the area of ![]() , which can be found by adding the areas of
, which can be found by adding the areas of ![]() and
and ![]() . It is trivial that
. It is trivial that ![]() and
and ![]() are congruent, so we know that
are congruent, so we know that ![]() . What we require is
. What we require is
We do similar calculations to obtain that ![]() and
and ![]() implies
implies ![]() , so now we plug in everything we know to calculate the area of the quadrilateral:
, so now we plug in everything we know to calculate the area of the quadrilateral:
We see that ![]() .
.
~ Edited by Aoum
Solution 5 (Circles and Trigonometry)
Since ![]() and
and ![]() , we can construct 2 circles of radus 14 with
, we can construct 2 circles of radus 14 with ![]() and
and ![]() as the center of the two circles. Let the intersection of the 2 circles other than
as the center of the two circles. Let the intersection of the 2 circles other than ![]() be point
be point ![]() . Connect
. Connect ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Connect
. Connect ![]() , which is the radical axis of the 2 circles.
, which is the radical axis of the 2 circles.
From the figure, we know that
![]()
![]()
Let ![]() , which means that
, which means that ![]() . For easier calculation, we temporarily define the radius of the 2 circles (which is 14) to be
. For easier calculation, we temporarily define the radius of the 2 circles (which is 14) to be ![]() .
. ![]() is an inscribed angle and
is an inscribed angle and ![]() is a central angle, so
is a central angle, so ![]() . Similar with the other side,
. Similar with the other side, ![]() .
. ![]() , so
, so ![]() is an equilateral triangle.
is an equilateral triangle.
Using the Law of Cosines, we get the area of each little triangle.
![]()
![]()
![]()
We can conclude that
![]()
![]()
Now, we just needed to find the value of ![]() . We analyze the
. We analyze the ![]() . We already know that
. We already know that ![]() and
and ![]() and
and ![]() . Using the Laws of Cosines (again!) and the given condition of
. Using the Laws of Cosines (again!) and the given condition of ![]() , we can create a formula on
, we can create a formula on ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
We put the calculated value of ![]() back into
back into ![]() :
:
![]()
![]()
Therefore,![]() .
.
~cassphe
Solution 6 (Trig Identities; warning: bashy)
Consider a diagram to the original problem (credit to solution 4):
![[asy] import math; import geometry; import olympiad; point A,B,C,L,K; A=(0,0); C=(16sqrt(3),0); B=(0,26); L=(8sqrt(3),2); K=(3sqrt(3),13); draw(A--B--C--cycle); draw(A--K--L--cycle); draw(B--K); draw(C--L); draw(B--L); label("A",A,SW); label("B",B,NW); label("C",C,SE); label("K",K,W); label("L",L,NE); markscalefactor=1; [/asy]](http://latex.artofproblemsolving.com/1/e/5/1e54b0430825127746ef64abd9465396b170bcfa.png)
Now, let us simplify the problem further. We know that ![]() and
and ![]() must lie on the perpendicular bisectors of
must lie on the perpendicular bisectors of ![]() and
and ![]() , respectively. The real problem here is the equilateral triangle in the middle, inscribed in a rectangle with diagonal length 19.
, respectively. The real problem here is the equilateral triangle in the middle, inscribed in a rectangle with diagonal length 19.
We create a further simplified problem: given that the inscribed equilateral triangle of a certain rectangle with diagonal length ![]() has side length
has side length ![]() , find the sides and intersection points on this rectangle. For reference, here is a diagram:
, find the sides and intersection points on this rectangle. For reference, here is a diagram:
![[asy] import math; import geometry; import olympiad; point A,B,C,D,L,K; A=(0,0); D=(13,0); B=(0,8sqrt(3)); C=(13,8sqrt(3)); L=(13,3sqrt(3)); K=(2,8sqrt(3)); draw(A--B--C--D--cycle); draw(A--K--L--cycle); label("A",A,SW); label("B",B,NW); label("C",C,NE); label("K",K,N); label("L",L,E); label("D",D,SE); markscalefactor=1; [/asy]](http://latex.artofproblemsolving.com/8/c/2/8c2b75f2411d0b8bfe2a293859ec71b296a58f28.png)
Note the angles ![]() and
and ![]() . Since
. Since ![]() ,
, ![]() , and
, and ![]() . Thus, let
. Thus, let ![]() and
and ![]() .
.
Now, we know that ![]() , as the hypotenuse of the larger right triangle is
, as the hypotenuse of the larger right triangle is ![]() . However, we can also express AB and AB in terms of
. However, we can also express AB and AB in terms of ![]() :
: ![]() and
and ![]() . Thus,
. Thus, ![]() . We expand this using the cosine difference identity:
. We expand this using the cosine difference identity:
![]()
![]()
Using the fact that ![]() , then multiplying the entire equation by
, then multiplying the entire equation by ![]() ,
,
![]()
Now, to save some writing, let us denote ![]() with
with ![]() , and
, and ![]() with
with ![]() .
.
We have the following equations:
![]()
![]()
Substituting ![]() for
for ![]() , moving
, moving ![]() to the left side, squaring, and dividing by 9, we end up with the quartic:
to the left side, squaring, and dividing by 9, we end up with the quartic:
![]()
Using the quadratic formula, we end up with this:
![]()
Now, we could just compute ![]() , but instead, we can do this:
, but instead, we can do this:
![]()
![]()
![]()
Thus, we have two cases:
![]()
![]()
Both lead to the same side lengths of the rectangle: ![]() , and
, and ![]() . Referring back to our original rectangle diagram and plugging in our trigonometric values, we get that
. Referring back to our original rectangle diagram and plugging in our trigonometric values, we get that ![]() , and
, and ![]() . Thus, the area of the original quadrilateral is
. Thus, the area of the original quadrilateral is ![]() , or
, or ![]() .
.
~Stead
Solution 7 (analytic geometry with roots of unity)
![[asy] import math; import geometry; import olympiad; point A,B,C,L,K; A=(0,0); C=(16sqrt(3),0); B=(0,26); L=(8sqrt(3),2); K=(3sqrt(3),13); point M,N; M=(8sqrt(3), 0); N=(0,13); draw(A--B--C--cycle); draw(A--K--L--cycle); draw(B--K); draw(C--L); draw(N--K); draw(L--M); label("A",A,SW); label("B",B,NW); label("C",C,SE); label("K",K,ENE); label("L",L,NE); label(“N”,N,W); label(“M”,M,S); point am, ml, an, nk, mc, bn; am=(4sqrt(3), 0); mc=(12sqrt(3),0); ml=(8sqrt(3),1); an=(0,6.5); bn=(0,19.5); nk=(2.5981, 13); label(“a",am,S); label(“a",mc,S); label(“y”,ml,ESE); label(“b”,an,W); label(“b”,bn,W); label(“x”,nk,S); markscalefactor=1; [/asy]](http://latex.artofproblemsolving.com/d/0/0/d007e59422f7d9ada71a9ed5e135c675087f9f1e.png) This diagram is modified from the solution 4 diagram. Let
This diagram is modified from the solution 4 diagram. Let ![]() be the midpoint of
be the midpoint of ![]() , and let
, and let ![]() be the midpoint of
be the midpoint of ![]() .
.
We place the diagram onto the Cartesian coordinate grid. Let ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . We are given
. We are given ![]() , so
, so ![]() is isosceles. Therefore,
is isosceles. Therefore, ![]() is the perpendicular bisector of
is the perpendicular bisector of ![]() , so we can let
, so we can let ![]() . Similarly, we’re given
. Similarly, we’re given ![]() , so
, so ![]() is also isosceles, and
is also isosceles, and ![]() is the perpendicular bisector of
is the perpendicular bisector of ![]() . Therefore, we can let
. Therefore, we can let ![]() .
.
We have ![]() and
and ![]() . We’re given that
. We’re given that ![]() and
and ![]() , so by the Pythagorean theorem,
, so by the Pythagorean theorem, ![]()
We now place the diagram onto the complex plane. We use the x-axis of the coordinate plane as the complex plane’s real axis, and we use the y-axis of the coordinate plane as the complex plane’s imaginary axis. So, on the complex plane, ![]() ,
, ![]() , and
, and ![]() . Also, since we are given
. Also, since we are given ![]() ,
, ![]() is equilateral. In addition, since
is equilateral. In addition, since ![]() ,
, ![]() , and because we constructed our diagram with
, and because we constructed our diagram with ![]() counterclockwise of
counterclockwise of ![]() (if it were the other way around, we could go through the same steps as this solution, but with variables switched around),
(if it were the other way around, we could go through the same steps as this solution, but with variables switched around), ![]() is a
is a ![]() counterclockwise rotation of
counterclockwise rotation of ![]() about
about ![]() , and
, and ![]() is a
is a ![]() clockwise or
clockwise or ![]() counterclockwise rotation of
counterclockwise rotation of ![]() about
about ![]() .
.
Rotation on the complex plane is equivalent to multiplying by a root of unity. Here, ![]() and
and ![]() are rotated a multiple of
are rotated a multiple of ![]() to each other about
to each other about ![]() .
. ![]() is one-sixth of a full circle, so to go from
is one-sixth of a full circle, so to go from ![]() to
to ![]() or
or ![]() to
to ![]() , we multiply by a 6th root of unity. Specifically, to go from
, we multiply by a 6th root of unity. Specifically, to go from ![]() to
to ![]() , we multiply by
, we multiply by ![]() , and to go from
, and to go from ![]() to
to ![]() , we multiply by
, we multiply by ![]() .
.
We multiply the coordinate of ![]() by
by ![]() on the complex plane to obtain equations for the coordinates of
on the complex plane to obtain equations for the coordinates of ![]() :
: ![\[(a + yi)\left(\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}i\right) = \left(\dfrac{a}{2} - \dfrac{\sqrt{3}}{2}y\right) + \left(\dfrac{y}{2} + \dfrac{\sqrt{3}}{2}a\right)i = x + bi.\]](http://latex.artofproblemsolving.com/0/d/5/0d5bc1d2894bdb97553533909d85c8d99a4eaa8e.png) Equating real and imaginary parts, we obtain
Equating real and imaginary parts, we obtain ![]()
Similarly, we multiply the coordinate of ![]() by
by ![]() to obtain equations for the coordinates of
to obtain equations for the coordinates of ![]() :
: ![\[(x + bi)\left(\dfrac{1}{2} - \dfrac{\sqrt{3}}{2}i\right) = \left(\dfrac{x}{2} + \dfrac{\sqrt{3}}{2}b\right) + \left(\dfrac{b}{2} - \dfrac{\sqrt{3}}{2}x\right) = a + yi.\]](http://latex.artofproblemsolving.com/f/7/1/f71aacd31bfa9cd1b0f414e85c54775f8dd12146.png) Equating real and imaginary parts, we obtain
Equating real and imaginary parts, we obtain ![]()
We now look back at the problem to see what it asks for: ![]() . Looking at the diagram, we see we can express the area of the quadrilateral as the area of the big right triangle
. Looking at the diagram, we see we can express the area of the quadrilateral as the area of the big right triangle ![]() minus the two isosceles triangles
minus the two isosceles triangles ![]() and
and ![]() minus the equilateral triangle
minus the equilateral triangle ![]() :
: ![]()
We are given that ![]() , so the area of equilateral triangle
, so the area of equilateral triangle ![]() is
is ![]() . Also, we can use
. Also, we can use ![]() as the base of
as the base of ![]() and
and ![]() as the height, so
as the height, so ![]() . Similarly, we use
. Similarly, we use ![]() as the base of
as the base of ![]() and
and ![]() (
(![]() and
and ![]() , so the distance between the two is equal to
, so the distance between the two is equal to ![]() ) as the height, so
) as the height, so ![]() . Finally, we use
. Finally, we use ![]() and
and ![]() (
(![]() and
and ![]() , so the distance between the two is equal to
, so the distance between the two is equal to ![]() ) as the base and height of
) as the base and height of ![]() respectively, so
respectively, so ![]() . Therefore,
. Therefore, ![]()
We have already shown that ![]() . Substituting this into
. Substituting this into ![]() , we have
, we have ![\[a^2 + \left(\dfrac{y}{2} + \dfrac{\sqrt{3}}{2}a\right)^2 = 361.\]](http://latex.artofproblemsolving.com/6/5/8/65870c5cf8c9baca1234d7bdd6a876c5dfacf8b8.png) Expanding this out, we have
Expanding this out, we have ![]() Multiplying both sides by
Multiplying both sides by ![]() and rearranging the left side, we have
and rearranging the left side, we have ![]() We previously showed that
We previously showed that ![]() , so
, so ![]() (since
(since ![]() is on
is on ![]() ). Therefore,
). Therefore, ![]() has a right angle at
has a right angle at ![]() . By the Pythagorean theorem,
. By the Pythagorean theorem, ![]() . Subtracting
. Subtracting ![]() from the left side and
from the left side and ![]() from the right side, we obtain
from the right side, we obtain ![]() Dividing both sides of the equation by
Dividing both sides of the equation by ![]() and factoring
and factoring ![]() out of the left side, we have
out of the left side, we have ![]() However, we have
However, we have ![]() , so the expression inside the parentheses is simply
, so the expression inside the parentheses is simply ![]() ! Therefore,
! Therefore, ![]()
The algebra’s not over yet. We also showed that ![]() , so substituting that into
, so substituting that into ![]() , we obtain
, we obtain ![\[b^2 + \left(\dfrac{x}{2} + \dfrac{\sqrt{3}}{2}b\right)^2 = 361.\]](http://latex.artofproblemsolving.com/1/8/e/18e59a695e6dceaa5916a848af13e3b829ab0178.png) Expanding this out, we have
Expanding this out, we have ![]() Multiplying both sides by
Multiplying both sides by ![]() and rearranging the left side, we now have
and rearranging the left side, we now have ![]() Does this equation look familiar? We previously showed that
Does this equation look familiar? We previously showed that ![]() . Therefore,
. Therefore, ![]() (since
(since ![]() is on
is on ![]() ). So,
). So, ![]() has a right angle at
has a right angle at ![]() . By the Pythagorean theorem,
. By the Pythagorean theorem, ![]() . Subtracting
. Subtracting ![]() from the left side and
from the left side and ![]() from the right side, we have
from the right side, we have ![]() We previously also had the equation
We previously also had the equation ![]() , and adding this equation to the above equation and factoring out
, and adding this equation to the above equation and factoring out ![]() , we have
, we have ![]() We previously showed
We previously showed ![]() , so
, so ![]() . Subtracting
. Subtracting ![]() from the left side and
from the left side and ![]() from the right side, we obtain
from the right side, we obtain ![]() . Finally, dividing both sides by
. Finally, dividing both sides by ![]() , we have
, we have ![]()
We previously arrived at this expression for ![]() :
: ![]() We now know
We now know ![]() and
and ![]() , so we can simply substitute them in. Therefore,
, so we can simply substitute them in. Therefore, ![]() Finally, we are given
Finally, we are given ![]() for some integer
for some integer ![]() . We know
. We know ![]() , so
, so ![]() .
.
Notice that ![]() . Is this a coincidence?
. Is this a coincidence?
~V0305
Solution 8
![]()
Similarly, ![]()
![]()
![]()
![]()
![]() Similarly,
Similarly, ![]()
Denote the area of triangle ![]() as
as ![]()
![]() Similarly,
Similarly, ![]()
![]() By applying the Law of Cosines on
By applying the Law of Cosines on ![]() we get
we get
![]()
![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Solution 9
![]() is clearly equilateral, and
is clearly equilateral, and ![]() and
and ![]() are clearly isosceles. Now, we can do a bit of angle chasing. Say
are clearly isosceles. Now, we can do a bit of angle chasing. Say ![]() . Then, since
. Then, since ![]() is isosceles,
is isosceles, ![]() .
. ![]() , so
, so ![]() , so
, so ![]() , so
, so ![]() . Since the angles are congruent,
. Since the angles are congruent, ![]() is congruent to
is congruent to ![]() . As such, we can rotate it around the center of
. As such, we can rotate it around the center of ![]() onto side AL to produce
onto side AL to produce ![]() . Because all the triangles are congruent, connecting the congruent corners will all produce the same length. From BC, we see that this length is
. Because all the triangles are congruent, connecting the congruent corners will all produce the same length. From BC, we see that this length is ![]() , so
, so ![]() is equilateral with side length
is equilateral with side length ![]() . This triangle is comprised of 3 quadrilaterals and
. This triangle is comprised of 3 quadrilaterals and ![]() in the center, and it's easy to see that each quadrilateral is congruent to
in the center, and it's easy to see that each quadrilateral is congruent to ![]() . As such,
. As such, ![]() , giving an answer of
, giving an answer of ![]() .
.
~noob1877
Video Solution (Angle chasing and congruent triangles)
https://youtu.be/APaVy8OqJ04?si=MSBv1fS1ajjqcxN6
Remarks
This problem can be approached either by analytic geometry or by trigonometric manipulation. The characteristics of this problem make it highly similar to 2017 AIME I Problem 15 (Link).
See also
| 2025 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()