Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Japanese Theorem"

(Undo revision 230989 by Charking (talk))
(Tag: Undo)
m (Stub)
 
(2 intermediate revisions by 2 users not shown)
Line 1: Line 1:
−
The '''Japanese theorem''' exists for both [[Cyclic_quadrilateral | cyclic quadrilaterals]] and [[Cyclic | cyclic polygons]].
+
The '''Japanese Theorem''' is a theorem which holds for [[cyclic polygon]]s.
  
−
==Japanese theorem for cyclic quadrilaterals==
+
== Statement ==
  
 +
For any triangulated cyclic polygon, the sum of the [[Inradius|inradii]] of the triangles is constant.
  
−
====Definition====
+
== Japanese Theorem for cyclic quadrilaterals ==
−
The '''Japanese theorem for cyclic quadrilaterals''' states that for a cyclic quadrilateral <math>ABCD</math> and [[Incenter | incenters]] <math>M_1</math>, <math>M_2</math>, <math>M_3</math>, <math>M_4</math> of triangles <math>\triangle ABD</math>, <math>\triangle ABC</math>, <math>\triangle BCD</math>, <math>\triangle ACD</math> the quadrilateral <math>M_1M_2M_3M_4</math> is a [[Rectangle | rectangle]].
 
  
 +
=== Statement ===
  
−
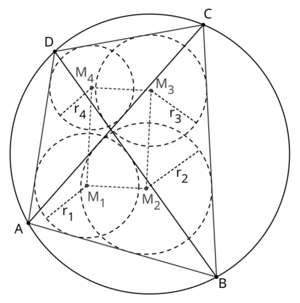
[[File:japanese_theorem_quadrilaterals.png|300px|thumb|left]]
+
The '''Japanese theorem for cyclic quadrilaterals''' states that for a cyclic quadrilateral <math>ABCD</math> and [[incenter]]s <math>M_1</math>, <math>M_2</math>, <math>M_3</math>, <math>M_4</math> of triangles <math>\triangle ABD</math>, <math>\triangle ABC</math>, <math>\triangle BCD</math>, <math>\triangle ACD</math> the quadrilateral <math>M_1M_2M_3M_4</math> is a [[rectangle]].
  
−
====Proof====
 
−
From <math>\triangle ABC</math>, we can see that
 
  
−
<math>\angle BM_2C = 90^{\circ} + \frac{1}{2} \angle CAB</math>
+
[[File:japanese_theorem_quadrilaterals.png|300px|thumb|left]]<!--Please Asymptote-->
  
−
Similarly, from <math>\triangle BCD</math> we have
+
=== Proof ===
−
 
 
−
<math>\angle BM_3C = 90^{\circ} + \frac{1}{2} \angle CDB</math>
 
  
 +
From <math>\triangle ABC</math>, we can see that
 +
<cmath>\angle BM_2C = 90^{\circ} + \frac{1}{2} \angle CAB</cmath>
 +
and similarly, from <math>\triangle BCD</math> we have
 +
<cmath>\angle BM_3C = 90^{\circ} + \frac{1}{2} \angle CDB</cmath>
 
Since <math>ABCD</math> is cyclic, therefore <math>\angle CDB = \angle CAB</math>, which means that
 
Since <math>ABCD</math> is cyclic, therefore <math>\angle CDB = \angle CAB</math>, which means that
−
 
+
<cmath>\angle BM_2C = \angle BM_3C</cmath>
−
<math>\angle BM_2C = \angle BM_3C</math>
 
−
 
 
 
From this, it follows that <math>BM_2M_3C</math> is cyclic. This means that
 
From this, it follows that <math>BM_2M_3C</math> is cyclic. This means that
−
 
+
<cmath>\angle BCM_3 + \angle BM_2M_3 = 180^{\circ}</cmath>
−
<math>\angle BCM_3 + \angle BM_2M_3 = 180^{\circ}</math>
 
−
 
 
 
By symmetry, we can also derive
 
By symmetry, we can also derive
−
 
+
<cmath>\angle BAM_1 + \angle BM_2M_1 = 180^{\circ}</cmath>
−
<math>\angle BAM_1 + \angle BM_2M_1 = 180^{\circ}</math>
+
Adding these equations, we get
−
 
+
<cmath>\angle BAM_1 + \angle BCM_3 + \angle BM_2M_1 + \angle BM_2M_3 = 360^{\circ}</cmath>
−
Adding these equations up, we get
+
<cmath>\implies \angle BM_2M_1 + \angle BM_2M_3 = 360^{\circ} - \angle BAM_1 - \angle BCM_3 = 360^{\circ} - \frac{1}{2} \left(\angle CAB + \angle CDB \right)</cmath>
−
 
 
−
<math>\angle BAM_1 + \angle BCM_3 + \angle BM_2M_1 + \angle BM_2M_3 = 360^{\circ}</math>
 
−
 
 
−
<math>\Rightarrow \angle BM_2M_1 + \angle BM_2M_3 = 360^{\circ} - \angle BAM_1 - \angle BCM_3 = 360^{\circ} - \frac{1}{2} \left(\angle CAB + \angle CDB \right)</math>
 
−
 
 
 
Which implies
 
Which implies
 +
<cmath>M_1M_2M_3 = 90^{\circ}</cmath>
  
−
<math>M_1M_2M_3 = 90^{\circ}</math>
+
And other angles similarly. <math>\square</math>
−
 
 
−
And other angles similarly.
 
−
 
 
−
<math>Q.E.D.</math>
 
−
 
 
−
 
 
−
==Japanese theorem for cyclic polygons==
 
−
 
 
  
−
====Definition====
+
{{stub}}
−
The '''Japanese theorem for cyclic polygons''' states that for any triangulated cyclic polygon, the sum of the [[Inradius || inradii]] of the triangles is constant.
 

Latest revision as of 09:46, 11 April 2025

The Japanese Theorem is a theorem which holds for cyclic polygons.

Statement

For any triangulated cyclic polygon, the sum of the inradii of the triangles is constant.

Japanese Theorem for cyclic quadrilaterals

Statement

The Japanese theorem for cyclic quadrilaterals states that for a cyclic quadrilateral $ABCD$ and incenters $M_1$, $M_2$, $M_3$, $M_4$ of triangles $\triangle ABD$, $\triangle ABC$, $\triangle BCD$, $\triangle ACD$ the quadrilateral $M_1M_2M_3M_4$ is a rectangle.


Japanese theorem quadrilaterals.png

Proof

From $\triangle ABC$, we can see that \[\angle BM_2C = 90^{\circ} + \frac{1}{2} \angle CAB\] and similarly, from $\triangle BCD$ we have \[\angle BM_3C = 90^{\circ} + \frac{1}{2} \angle CDB\] Since $ABCD$ is cyclic, therefore $\angle CDB = \angle CAB$, which means that \[\angle BM_2C = \angle BM_3C\] From this, it follows that $BM_2M_3C$ is cyclic. This means that \[\angle BCM_3 + \angle BM_2M_3 = 180^{\circ}\] By symmetry, we can also derive \[\angle BAM_1 + \angle BM_2M_1 = 180^{\circ}\] Adding these equations, we get \[\angle BAM_1 + \angle BCM_3 + \angle BM_2M_1 + \angle BM_2M_3 = 360^{\circ}\] \[\implies \angle BM_2M_1 + \angle BM_2M_3 = 360^{\circ} - \angle BAM_1 - \angle BCM_3 = 360^{\circ} - \frac{1}{2} \left(\angle CAB + \angle CDB \right)\] Which implies \[M_1M_2M_3 = 90^{\circ}\]

And other angles similarly. $\square$

This article is a stub. Help us out by expanding it.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Japanese_Theorem&oldid=246547"