Difference between revisions of "2024 AMC 10A Problems/Problem 19"
(Solutions) |
|||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
==Problem== | ==Problem== | ||
| − | + | A bee is moving in three-dimensional space. A fair six-sided die with faces labeled <math>A^{+}, A^{-}, B^{+}, B^{-}, C^{+}</math>, and <math>C^{-}</math> is rolled. Suppose the bee occupies the point <math>(a, b, c)</math>. If the die shows <math>A^{+}</math>, then the bee moves to the point <math>(a + 1, b, c)</math> and if the die shows <math>A^{-}</math>, then the bee moves to the point <math>(a - 1, b, c)</math>. Analogous moves are made with the other four outcomes. Suppose the bee starts at the point <math>(0, 0, 0)</math> and the die is rolled four times. What is the probability that the bee traverses four distinct edges of some unit cube? | |
| − | |||
| − | <math> | ||
| − | |||
| − | |||
| − | |||
| − | + | <math>\textbf{(A)}~\frac{1}{54}\qquad\textbf{(B)}~\frac{7}{54}\qquad\textbf{(C)}~\frac{1}{6}\qquad\textbf{(D)}~\frac{5}{18}\qquad\textbf{(E)}~\frac{2}{5}</math> | |
| − | + | == Diagrams == | |
| + | [[Image:Diagrams.jpeg|200px]] | ||
| + | [[File:Bee total.png|600px|right]] | ||
| + | ~ Diagram by PaperMath | ||
| − | + | [[Image:2024amc10a24solution.jpg|300px]] | |
| − | + | ~ Solution diagram by juwushu | |
| − | + | == Solution 1 == | |
| + | WLOG, assume that the first two moves are equal for all possible combinations, since the direction does not matter. The first move has a <math>\frac{6}{6}</math> probability of being along one of the <math>8</math> unit cubes around the origin, and the second move has a <math>\frac{4}{6}</math> chance. | ||
| + | Now, there are two cases. We are currently on one of the points of the <math>2</math> by <math>2</math> squares that are aligned with the axes. | ||
| + | The first case is if the bee moves to the corner of a cube farthest away from the origin. | ||
| + | Here, there is a <math>\frac{2}{6}</math> chance of this happening and a <math>\frac{2}{6}</math> chance of the fourth move remaining on one of the cubes. | ||
| + | The second case is if the bee moves along the same plane of the <math>2</math> by <math>2</math> squares previously, ending up on a point 1 away from the origin. There is a <math>\frac{1}{6}</math> chance of this happening and a <math>\frac{3}{6}</math> chance of remaining on one of the cubes. | ||
| + | Now, multiply and sum for the answer. | ||
| + | <cmath>\frac{2}{3}\cdot(\frac{1}{3}\cdot\frac{1}{3}+\frac{1}{6}\cdot\frac{1}{2})=\frac{2}{3}\cdot(\frac{1}{9}+\frac{1}{12})</cmath> | ||
| + | Evaluating this gives you the answer of <math>\boxed{\textbf{(B) }\frac{7}{54}}</math>. | ||
| + | Solution by [[User:Juwushu|juwushu]]. | ||
| + | Minor edits by andliu766 | ||
==Solution 2== | ==Solution 2== | ||
| − | + | Remove the dice. It is not necessary for this problem. It is the same problem if you instead view this problem as the bee moving one up or down in the <math>x, y,</math> and <math>z</math> directions. | |
| − | |||
| − | |||
| − | + | Count the total number of ways for one cube of the 8 total ones. It is not hard to see that after the first step (which you can travel to <math>(1,0,0), (0,1,0),</math> or <math>(0,0,1)</math> - 3 ways), you have a total of 8 moves to traverse a face of that 1x1 cube. Hence, for each cube, you would have <math>8 \cdot 3 = 24</math> total moves. | |
| − | + | There are a total of 8 cubes you could have traversed, though, so multiplying this by <math>8</math> yields <math>8 \cdot 8 \cdot 3.</math> | |
| − | + | We have to account for overcounting. For example, when we traversed the face in the <math>xz</math> plane <math>(0,0,0), (0,0,1),(1,0,0),(1,0,1),</math> the number of ways that we traverse that particular face got counted twice, once from the cube in the far upper right and once from the cube in the closer upper right. | |
| − | = | + | For a given face, you can go clockwise or counterclockwise, hence yielding <math>2</math> ways. There are a total of <math>12</math> shared faces, each one shared by exactly two faces so no additonal PIE is needed. We simply subtract <math>2\cdot12</math> from our original count now, yielding <math>8 \cdot 3 \cdot 8 - 2 \cdot 12 = 168.</math> |
| − | + | With no restrictions, there are a total of <math>6^4</math> ways to move four steps. Your probability is <math>\frac{168}{6^4}=\frac{7}{54}.</math> | |
| − | ~ | + | ~mathboy282 |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Video Solution by Power Solve == | == Video Solution by Power Solve == | ||
| − | https://www.youtube.com/watch?v= | + | https://www.youtube.com/watch?v=2uTWPiWzfB0 |
| − | ==Video Solution by | + | == Video Solution by Pi Academy (Fast and Easy ⚡️🚀) == |
| − | |||
| − | = | + | https://youtu.be/3Dk-vmdxbrw?si=G6TcyLN2Rfwd2YYJ |
| − | https:// | + | ==Video Solution by Innovative Minds== |
| + | https://youtu.be/CxLGUPhYYDI | ||
| − | + | ~i_am_suk_at_math_2 | |
| − | |||
| − | |||
==Video Solution by SpreadTheMathLove== | ==Video Solution by SpreadTheMathLove== | ||
| Line 67: | Line 58: | ||
==See also== | ==See also== | ||
{{AMC10 box|year=2024|ab=A|num-b=18|num-a=20}} | {{AMC10 box|year=2024|ab=A|num-b=18|num-a=20}} | ||
| − | |||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 21:28, 20 March 2025
Contents
[hide]Problem
A bee is moving in three-dimensional space. A fair six-sided die with faces labeled ![]() , and
, and ![]() is rolled. Suppose the bee occupies the point
is rolled. Suppose the bee occupies the point ![]() . If the die shows
. If the die shows ![]() , then the bee moves to the point
, then the bee moves to the point ![]() and if the die shows
and if the die shows ![]() , then the bee moves to the point
, then the bee moves to the point ![]() . Analogous moves are made with the other four outcomes. Suppose the bee starts at the point
. Analogous moves are made with the other four outcomes. Suppose the bee starts at the point ![]() and the die is rolled four times. What is the probability that the bee traverses four distinct edges of some unit cube?
and the die is rolled four times. What is the probability that the bee traverses four distinct edges of some unit cube?
![]()
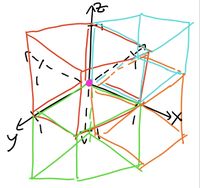
Diagrams
~ Diagram by PaperMath
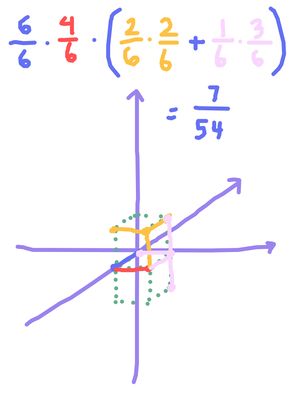
~ Solution diagram by juwushu
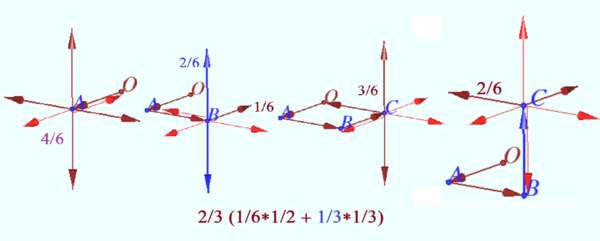
Solution 1
WLOG, assume that the first two moves are equal for all possible combinations, since the direction does not matter. The first move has a ![]() probability of being along one of the
probability of being along one of the ![]() unit cubes around the origin, and the second move has a
unit cubes around the origin, and the second move has a ![]() chance.
Now, there are two cases. We are currently on one of the points of the
chance.
Now, there are two cases. We are currently on one of the points of the ![]() by
by ![]() squares that are aligned with the axes.
The first case is if the bee moves to the corner of a cube farthest away from the origin.
Here, there is a
squares that are aligned with the axes.
The first case is if the bee moves to the corner of a cube farthest away from the origin.
Here, there is a ![]() chance of this happening and a
chance of this happening and a ![]() chance of the fourth move remaining on one of the cubes.
The second case is if the bee moves along the same plane of the
chance of the fourth move remaining on one of the cubes.
The second case is if the bee moves along the same plane of the ![]() by
by ![]() squares previously, ending up on a point 1 away from the origin. There is a
squares previously, ending up on a point 1 away from the origin. There is a ![]() chance of this happening and a
chance of this happening and a ![]() chance of remaining on one of the cubes.
Now, multiply and sum for the answer.
chance of remaining on one of the cubes.
Now, multiply and sum for the answer.
![]() Evaluating this gives you the answer of
Evaluating this gives you the answer of ![]() .
Solution by juwushu.
Minor edits by andliu766
.
Solution by juwushu.
Minor edits by andliu766
Solution 2
Remove the dice. It is not necessary for this problem. It is the same problem if you instead view this problem as the bee moving one up or down in the ![]() and
and ![]() directions.
directions.
Count the total number of ways for one cube of the 8 total ones. It is not hard to see that after the first step (which you can travel to ![]() or
or ![]() - 3 ways), you have a total of 8 moves to traverse a face of that 1x1 cube. Hence, for each cube, you would have
- 3 ways), you have a total of 8 moves to traverse a face of that 1x1 cube. Hence, for each cube, you would have ![]() total moves.
total moves.
There are a total of 8 cubes you could have traversed, though, so multiplying this by ![]() yields
yields ![]()
We have to account for overcounting. For example, when we traversed the face in the ![]() plane
plane ![]() the number of ways that we traverse that particular face got counted twice, once from the cube in the far upper right and once from the cube in the closer upper right.
the number of ways that we traverse that particular face got counted twice, once from the cube in the far upper right and once from the cube in the closer upper right.
For a given face, you can go clockwise or counterclockwise, hence yielding ![]() ways. There are a total of
ways. There are a total of ![]() shared faces, each one shared by exactly two faces so no additonal PIE is needed. We simply subtract
shared faces, each one shared by exactly two faces so no additonal PIE is needed. We simply subtract ![]() from our original count now, yielding
from our original count now, yielding ![]()
With no restrictions, there are a total of ![]() ways to move four steps. Your probability is
ways to move four steps. Your probability is ![]()
~mathboy282
Video Solution by Power Solve
https://www.youtube.com/watch?v=2uTWPiWzfB0
Video Solution by Pi Academy (Fast and Easy ⚡️🚀)
https://youtu.be/3Dk-vmdxbrw?si=G6TcyLN2Rfwd2YYJ
Video Solution by Innovative Minds
~i_am_suk_at_math_2
Video Solution by SpreadTheMathLove
https://www.youtube.com/watch?v=6SQ74nt3ynw
See also
| 2024 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 18 |
Followed by Problem 20 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()