Difference between revisions of "2024 AMC 10A Problems"
MRENTHUSIASM (talk | contribs) |
|||
| Line 2: | Line 2: | ||
==Problem 1== | ==Problem 1== | ||
| − | + | What is the value of <math>9901 \cdot 101 - 99 \cdot 10101</math>? | |
| − | What is the value of <math>9901\ | ||
<math>\textbf{(A)}~2\qquad\textbf{(B)}~20\qquad\textbf{(C)}~200\qquad\textbf{(D)}~202\qquad\textbf{(E)}~2020</math> | <math>\textbf{(A)}~2\qquad\textbf{(B)}~20\qquad\textbf{(C)}~200\qquad\textbf{(D)}~202\qquad\textbf{(E)}~2020</math> | ||
| Line 10: | Line 9: | ||
==Problem 2== | ==Problem 2== | ||
| + | Define <math>\blacktriangledown(a) = \sqrt{a - 1}</math> and <math>\blacktriangle(a) = \sqrt{a + 1}</math> for all real numbers <math>a</math>. What is the value of <cmath>\frac{\blacktriangledown(20 + \blacktriangle(2024))}{\blacktriangledown(\blacktriangle(24))}~?</cmath> | ||
| − | + | <math>\textbf{(A)}~ 1 \qquad \textbf{(B)}~ 2 \qquad \textbf{(C)}~ 4 \qquad \textbf{(D)}~ 8 \qquad \textbf{(E)}~ 16</math> | |
| − | |||
| − | <math>\textbf{(A) } | ||
[[2024 AMC 10A Problems/Problem 2|Solution]] | [[2024 AMC 10A Problems/Problem 2|Solution]] | ||
==Problem 3== | ==Problem 3== | ||
| − | |||
What is the sum of the digits of the smallest prime that can be written as a sum of <math>5</math> distinct primes? | What is the sum of the digits of the smallest prime that can be written as a sum of <math>5</math> distinct primes? | ||
| − | <math>\textbf{(A) }5\qquad\textbf{(B) }7\qquad\textbf{(C) } | + | <math>\textbf{(A)}~5\qquad\textbf{(B)}~7\qquad\textbf{(C)}~9\qquad\textbf{(D)}~10\qquad\textbf{(E)}~11</math> |
[[2024 AMC 10A Problems/Problem 3|Solution]] | [[2024 AMC 10A Problems/Problem 3|Solution]] | ||
==Problem 4== | ==Problem 4== | ||
| + | A square and an isosceles triangle are joined along an edge to form a pentagon <math>10</math> inches tall and <math>22</math> inches wide, as shown below. What is the perimeter of the pentagon, in inches? | ||
| − | + | <asy> | |
| + | import graph; size(7cm); | ||
| + | real labelscalefactor = 0.5; /* changes label-to-point distance */ | ||
| + | pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ | ||
| + | pen dotstyle = black; /* point style */ | ||
| + | pen GGG = grey; | ||
| + | draw((10, 0)--(0, 0)--(0, 10)--(10, 10)); | ||
| + | draw((10, 0)--(10, 10), dashed); | ||
| + | draw((10, 0)--(22, 5)--(10, 10)); | ||
| + | draw((-1.5, 0)--(-1.5, 10), arrow = ArcArrow(SimpleHead), GGG); | ||
| + | draw((-1.5, 10)--(-1.5, 0), arrow = ArcArrow(SimpleHead), GGG); | ||
| + | draw((0, 11.5)--(22, 11.5), arrow = ArcArrow(SimpleHead), GGG); | ||
| + | draw((22, 11.5)--(0, 11.5), arrow = ArcArrow(SimpleHead), GGG); | ||
| + | label("$10$ in.", (-3.5, 5), GGG); | ||
| + | label("$22$ in.", (11, 12.75), GGG); | ||
| + | dot((0, 0)); | ||
| + | dot((0, 10)); | ||
| + | dot((10, 10)); | ||
| + | dot((10, 0)); | ||
| + | dot((22, 5)); | ||
| + | </asy> | ||
| − | <math>\textbf{(A) } | + | <math>\textbf{(A)}~54\qquad \textbf{(B)}~56 \qquad \textbf{(C)}~62 \qquad \textbf{(D)}~64 \qquad \textbf{(E)}~66</math> |
[[2024 AMC 10A Problems/Problem 4|Solution]] | [[2024 AMC 10A Problems/Problem 4|Solution]] | ||
==Problem 5== | ==Problem 5== | ||
| + | Andrea is taking a series of several exams. If Andrea earns <math>61</math> points on her next exam, her average score will decrease by <math>3</math> points. If she instead earns <math>93</math> points on her next exam, her average score will increase by <math>1</math> point. How many points should Andrea earn on her next exam to keep her average score constant? | ||
| − | + | <math>\textbf{(A)}~80 \qquad\textbf{(B)}~82 \qquad\textbf{(C)}~83 \qquad\textbf{(D)}~85 \qquad\textbf{(E)}~86</math> | |
| − | |||
| − | <math>\textbf{(A) } | ||
[[2024 AMC 10A Problems/Problem 5|Solution]] | [[2024 AMC 10A Problems/Problem 5|Solution]] | ||
==Problem 6== | ==Problem 6== | ||
| + | How many ordered pairs <math>(m, n)</math> of positive integers exist such that <math>m</math> is a factor of <math>54</math> and <math>mn</math> is a factor of <math>70</math>? | ||
| − | + | <math>\textbf{(A)}~2 \qquad\textbf{(B)}~4 \qquad\textbf{(C)}~10 \qquad\textbf{(D)}~12 \qquad\textbf{(E)}~16</math> | |
| − | |||
| − | |||
| − | <math>\textbf{(A)}~ | ||
[[2024 AMC 10A Problems/Problem 6|Solution]] | [[2024 AMC 10A Problems/Problem 6|Solution]] | ||
==Problem 7== | ==Problem 7== | ||
| + | Let <math>M</math> be the midpoint of segment <math>\overline{AB}</math>, and let <math>T</math> lie on segment <math>\overline{AB}</math> so that <math>AT \cdot AM = 100</math> and <math>BT \cdot BM = 28</math>. What is the length of segment <math>\overline{TM}</math>? | ||
| − | + | <math>\textbf{(A)}~4\qquad \textbf{(B)}~4.5\qquad \textbf{(C)}~5 \qquad \textbf{(D)}~5.5 \qquad \textbf{(E)}~6</math> | |
| − | |||
| − | |||
| − | <math>\textbf{(A) } | ||
[[2024 AMC 10A Problems/Problem 7|Solution]] | [[2024 AMC 10A Problems/Problem 7|Solution]] | ||
==Problem 8== | ==Problem 8== | ||
| + | In how many ways can <math>6</math> juniors and <math>6</math> seniors form <math>3</math> disjoint teams of <math>4</math> people so | ||
| + | that each team has <math>2</math> juniors and <math>2</math> seniors? | ||
| − | + | <math>\textbf{(A)}~720\qquad\textbf{(B)}~1350\qquad\textbf{(C)}~2700\qquad\textbf{(D)}~3280\qquad\textbf{(E)}~8100</math> | |
| − | |||
| − | <math>\textbf{(A) } | ||
[[2024 AMC 10A Problems/Problem 8|Solution]] | [[2024 AMC 10A Problems/Problem 8|Solution]] | ||
==Problem 9== | ==Problem 9== | ||
| + | Let <math>N</math> be the least positive integer that is divisible by at least <math>3</math> odd primes and at least <math>4</math> perfect squares. What is the sum of the squares of the digits of <math>N</math>? | ||
| − | + | <math>\textbf{(A)}~ 41 \qquad \textbf{(B)}~ 65 \qquad \textbf{(C)}~ 80 \qquad \textbf{(D)}~ 89 \qquad \textbf{(E)}~ 100</math> | |
| − | |||
| − | |||
| − | <math>\textbf{(A) } | ||
[[2024 AMC 10A Problems/Problem 9|Solution]] | [[2024 AMC 10A Problems/Problem 9|Solution]] | ||
==Problem 10== | ==Problem 10== | ||
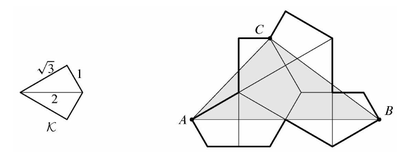
| + | Let <math>\mathcal{K}</math> be the kite formed by joining two right triangles with legs <math>1</math> and <math>\sqrt{3}</math> along a common hypotenuse. Eight copies of <math>\mathcal{K}</math> are used to form the polygon shown below. What is the area of triangle <math>\triangle ABC</math>? | ||
| + | |||
| + | [[File:Screenshot_2024-11-08_3.23.29_PM.png|400px|center]] | ||
| − | + | <math>\textbf{(A)}~2 + 3\sqrt{3} \qquad\textbf{(B)}~\frac{9\sqrt{3}}{2} \qquad\textbf{(C)}~\frac{10 + 8\sqrt{3}}{3} \qquad\textbf{(D)}~8 \qquad\textbf{(E)}~5\sqrt{3}</math> | |
| − | |||
| − | |||
[[2024 AMC 10A Problems/Problem 10|Solution]] | [[2024 AMC 10A Problems/Problem 10|Solution]] | ||
==Problem 11== | ==Problem 11== | ||
| + | If <math>x</math> and <math>y</math> are real numbers satisfying <math>x + \tfrac{x}{y} = 2</math> and <math>y + \tfrac{y}{x} = 6</math>, what is the value of <math>x + y</math>? | ||
| − | + | <math>\textbf{(A)}~\frac{101}{28} \qquad\textbf{(B)}~\frac{42}{11} \qquad\textbf{(C)}~\frac{30}{7} \qquad\textbf{(D)}~\frac{14}{3} \qquad\textbf{(E)}~\frac{110}{21}</math> | |
| − | |||
| − | <math>\textbf{(A)}~ | ||
[[2024 AMC 10A Problems/Problem 11|Solution]] | [[2024 AMC 10A Problems/Problem 11|Solution]] | ||
==Problem 12== | ==Problem 12== | ||
| + | Square <math>ABCD</math> has side length <math>6</math> and center <math>O</math>. Points <math>E</math> and <math>F</math> lie in the plane, and <math>AOEF</math> is a rectangle. Suppose that exactly <math>\tfrac{2}{3}</math> of the area of <math>AOEF</math> lies inside square <math>ABCD</math>. What is the area of <math>\triangle CEF</math>? | ||
| − | + | <math>\textbf{(A)}~4\qquad\textbf{(B)}~3\sqrt{2}\qquad\textbf{(C)}~6\qquad\textbf{(D)}~4\sqrt{3}\qquad\textbf{(E)}~8</math> | |
| − | |||
| − | <math>\textbf{(A)}~ | ||
[[2024 AMC 10A Problems/Problem 12|Solution]] | [[2024 AMC 10A Problems/Problem 12|Solution]] | ||
==Problem 13== | ==Problem 13== | ||
| − | + | Aubrey raced his younger brother Blair. Aubrey runs at a faster constant speed than Blair, so Blair started the race <math>40</math> feet ahead of Aubrey. Aubrey caught up to Blair after <math>8</math> seconds, finishing the race <math>90</math> feet ahead of Blair and <math>5</math> seconds earlier than Blair. How far did Aubrey run, in feet? | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <math>\textbf{(A)}~ | + | <math>\textbf{(A)}~454\qquad\textbf{(B)}~494\qquad\textbf{(C)}~518\qquad\textbf{(D)}~558\qquad\textbf{(E)}~598</math> |
[[2024 AMC 10A Problems/Problem 13|Solution]] | [[2024 AMC 10A Problems/Problem 13|Solution]] | ||
==Problem 14== | ==Problem 14== | ||
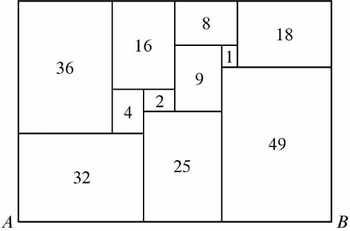
| + | All of the rectangles in the figure below, which is drawn to scale, are similar to the enclosing rectangle. Each number represents the area of the rectangle. What is the length <math>AB</math>? | ||
| − | + | [[File:Screenshot 2024-11-08 2.08.49 PM.png|350px|center]] | |
| − | <math>\textbf{(A)}~ | + | <math>\textbf{(A)}~4 + 4\sqrt{5}\qquad\textbf{(B)}~10\sqrt{2}\qquad\textbf{(C)}~5 + 5\sqrt{5}\qquad\textbf{(D)}~10\sqrt[4]{8}\qquad\textbf{(E)}~20</math> |
[[2024 AMC 10A Problems/Problem 14|Solution]] | [[2024 AMC 10A Problems/Problem 14|Solution]] | ||
==Problem 15== | ==Problem 15== | ||
| + | Let <math>S</math> be a subset of <math>\{1, 2, 3, \cdots, 2024\}</math> such that the following two conditions hold: | ||
| − | + | * If <math>x</math> and <math>y</math> are distinct elements of <math>S</math>, then <math>|x - y| > 2</math>. | |
| + | * If <math>x</math> and <math>y</math> are distinct odd elements of <math>S</math>, then <math>|x - y| > 6</math>. | ||
| − | <math>\textbf{(A) } | + | What is the maximum possible number of elements in <math>S</math>? |
| + | |||
| + | <math>\textbf{(A)}~436\qquad\textbf{(B)}~506\qquad\textbf{(C)}~608\qquad\textbf{(D)}~654\qquad\textbf{(E)}~675</math> | ||
[[2024 AMC 10A Problems/Problem 15|Solution]] | [[2024 AMC 10A Problems/Problem 15|Solution]] | ||
==Problem 16== | ==Problem 16== | ||
| + | In how many ways can the integers <math>1</math>, <math>2</math>, <math>3</math>, <math>4</math>, <math>5</math>, and <math>6</math> be arranged in a line so that the following statement is true? If <math>2</math> is not adjacent to <math>3</math>, then <math>3</math> is not adjacent to <math>4</math>. | ||
| − | + | <math>\textbf{(A)}~480 \qquad\textbf{(B)}~504 \qquad\textbf{(C)}~528 \qquad\textbf{(D)}~572 \qquad\textbf{(E)}~600</math> | |
| − | |||
| − | <math>\textbf{(A) } | ||
[[2024 AMC 10A Problems/Problem 16|Solution]] | [[2024 AMC 10A Problems/Problem 16|Solution]] | ||
==Problem 17== | ==Problem 17== | ||
| + | The numbers, in order, of each row and the numbers, in order, of each column of a <math>5 \times 5</math> array of integers form an arithmetic progression of length <math>5</math>. The numbers in positions <math>(5, 5)</math>, <math>(2, 4)</math>, <math>(4, 3)</math>, and <math>(3, 1)</math> are <math>0</math>, <math>48</math>, <math>16</math>, and <math>12</math>, respectively. What number is in position <math>(1, 2)</math>? <cmath> | ||
| − | + | <math>\textbf{(A)}~19\qquad\textbf{(B)}~24\qquad\textbf{(C)}~29\qquad\textbf{(D)}~34\qquad\textbf{(E)}~39</math> | |
| − | |||
| − | <math>\textbf{(A)}~ | ||
[[2024 AMC 10A Problems/Problem 17|Solution]] | [[2024 AMC 10A Problems/Problem 17|Solution]] | ||
==Problem 18== | ==Problem 18== | ||
| + | Points <math>X</math> and <math>Y</math> lie on sides <math>\overline{BC}</math> and <math>\overline{CD}</math>, respectively, of parallelogram <math>ABCD</math> such that <math>\angle AXC = \angle AYC = 90^{\circ}</math>. Suppose <math>BX = 5</math> and <math>DY = 3</math>, as shown. If <math>ABCD</math> has perimeter <math>48</math>, what is its area? | ||
| − | + | <asy> | |
| + | import olympiad; import graph; | ||
| + | size(8cm); | ||
| + | real labelscalefactor = 0.5; /* changes label-to-point distance */ | ||
| + | pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ | ||
| + | pen dotstyle = black; /* point style */ | ||
| + | pair A = (0, 0), B = (15, 0), C = (12, -6 * sqrt(2)), D = (-3, -6 * sqrt(2)); | ||
| + | pair X = (15 - 3 * 5/9, -6 * sqrt(2) * 5 / 9); | ||
| + | pair Y = (0, -6 * sqrt(2)); | ||
| + | dot(A); dot(B); dot(C); dot(D); dot(X); dot(Y); | ||
| + | draw(A--B--C--D--cycle); | ||
| + | draw(A--X); draw(A--Y); | ||
| + | draw(rightanglemark(A,X,C,15)); draw(rightanglemark(A,Y,C,15)); | ||
| + | label("$A$", A, N * 1.5); | ||
| + | label("$B$", B, N * 1.5); | ||
| + | label("$C$", C, S * 1.5); | ||
| + | label("$D$", D, S * 1.5); | ||
| + | label("$X$", X, E * 1.5); | ||
| + | label("$Y$", Y, S * 1.5); | ||
| + | label("$3$", midpoint(D--Y), S * 1.5); | ||
| + | label("$5$", midpoint(B--X), E * 1.5); | ||
| + | </asy> | ||
| − | <math>\textbf{(A)}~ | + | <math>\textbf{(A)}~40\sqrt{5}\qquad\textbf{(B)}~56\sqrt{3}\qquad\textbf{(C)}~48\sqrt{7}\qquad\textbf{(D)}~90\sqrt{2}\qquad\textbf{(E)}~60\sqrt{5}</math> |
[[2024 AMC 10A Problems/Problem 18|Solution]] | [[2024 AMC 10A Problems/Problem 18|Solution]] | ||
==Problem 19== | ==Problem 19== | ||
| + | A bee is moving in three-dimensional space. A fair six-sided die with faces labeled <math>A^{+}, A^{-}, B^{+}, B^{-}, C^{+}</math>, and <math>C^{-}</math> is rolled. Suppose the bee occupies the point <math>(a, b, c)</math>. If the die shows <math>A^{+}</math>, then the bee moves to the point <math>(a + 1, b, c)</math> and if the die shows <math>A^{-}</math>, then the bee moves to the point <math>(a - 1, b, c)</math>. Analogous moves are made with the other four outcomes. Suppose the bee starts at the point <math>(0, 0, 0)</math> and the die is rolled four times. What is the probability that the bee traverses four distinct edges of some unit cube? | ||
| − | + | <math>\textbf{(A)}~\frac{1}{54}\qquad\textbf{(B)}~\frac{7}{54}\qquad\textbf{(C)}~\frac{1}{6}\qquad\textbf{(D)}~\frac{5}{18}\qquad\textbf{(E)}~\frac{2}{5}</math> | |
| − | |||
| − | <math>\textbf{(A) } | ||
[[2024 AMC 10A Problems/Problem 19|Solution]] | [[2024 AMC 10A Problems/Problem 19|Solution]] | ||
==Problem 20== | ==Problem 20== | ||
| + | Point <math>X</math> lies outside regular pentagon <math>ABCDE</math> so that <math>\triangle BXE</math> is an equilateral triangle, as shown below. What is the degree measure of acute angle <math>\angle CXD</math>? | ||
| − | + | <asy> | |
| + | import graph; size(7cm); | ||
| + | real labelscalefactor = 0.75; /* changes label-to-point distance */ | ||
| + | pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ | ||
| + | pen dotstyle = black; /* point style */ | ||
| + | real xmin = -1.089556028373145, xmax = 2.738320502950249, ymin = -1.3143096399343266, ymax = 1.2691431521185288; /* image dimensions */ | ||
| + | pen qqwuqq = rgb(0,0.39215686274509803,0); | ||
| − | * | + | filldraw(arc((1.9562952014676112,0),0.25,168,192)--(1.9562952014676112,0)--cycle, mediumgrey); |
| − | + | /* draw figures */ | |
| − | * | + | draw((-0.8090169943749473,0.5877852522924731)--(0.30901699437494745,0.9510565162951535)); |
| − | + | draw((0.30901699437494745,0.9510565162951535)--(1,0)); | |
| − | + | draw((1,0)--(0.3090169943749473,-0.9510565162951536)); | |
| + | draw((0.3090169943749473,-0.9510565162951536)--(-0.8090169943749475,-0.587785252292473)); | ||
| + | draw((-0.8090169943749475,-0.587785252292473)--(-0.8090169943749473,0.5877852522924731)); | ||
| + | draw((0.30901699437494745,0.9510565162951535)--(0.3090169943749473,-0.9510565162951536)); | ||
| + | draw((0.3090169943749473,-0.9510565162951536)--(1.9562952014676112,0)); | ||
| + | draw((1.9562952014676112,0)--(0.30901699437494745,0.9510565162951535)); | ||
| + | draw((-0.8090169943749473,0.5877852522924731)--(1.9562952014676112,0), dashed); | ||
| + | draw((1.9562952014676112,0)--(-0.8090169943749475,-0.587785252292473), dashed); | ||
| + | /* dots and labels */ | ||
| + | dot((1,0),linewidth(4pt) + dotstyle); | ||
| + | label("$A$", (1.013592864312142,0), E * labelscalefactor); | ||
| + | dot((0.30901699437494745,0.9510565162951535),linewidth(4pt) + dotstyle); | ||
| + | label("$B$", (0.26,1), NE * labelscalefactor); | ||
| + | dot((-0.8090169943749473,0.5877852522924731),linewidth(4pt) + dotstyle); | ||
| + | label("$C$", (-0.82,0.64), NW * 0.25); | ||
| + | dot((-0.8090169943749475,-0.587785252292473),linewidth(4pt) + dotstyle); | ||
| + | label("$D$", (-0.82,-0.64), SW * 0.25); | ||
| + | dot((0.3090169943749473,-0.9510565162951536),linewidth(4pt) + dotstyle); | ||
| + | label("$E$", (0.26,-1), SE * labelscalefactor); | ||
| + | dot((1.9562952014676112,0),linewidth(4pt) + dotstyle); | ||
| + | label("$X$", (1.9705619971429902, 0), E * labelscalefactor); | ||
| + | clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle); | ||
| + | /* end of picture */ | ||
| + | </asy> | ||
| − | <math>\textbf{(A) } | + | <math>\textbf{(A)}~18^{\circ}\qquad\textbf{(B)}~19.5^{\circ}\qquad\textbf{(C)}~21^{\circ}\qquad\textbf{(D)}~22.5^{\circ}\qquad\textbf{(E)}~24^{\circ}</math> |
[[2024 AMC 10A Problems/Problem 20|Solution]] | [[2024 AMC 10A Problems/Problem 20|Solution]] | ||
==Problem 21== | ==Problem 21== | ||
| + | A fair six-sided die is repeatedly rolled until the same number is rolled twice in a row. What is the probability that the last number rolled is equal to the first number rolled? | ||
| − | + | <math>\textbf{(A)}~\frac{17}{72} \qquad\textbf{(B)}~\frac{4}{15} \qquad\textbf{(C)}~\frac{5}{18} \qquad\textbf{(D)}~\frac{2}{7} \qquad\textbf{(E)}~\frac{3}{10}</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
[[2024 AMC 10A Problems/Problem 21|Solution]] | [[2024 AMC 10A Problems/Problem 21|Solution]] | ||
==Problem 22== | ==Problem 22== | ||
| + | Let <math>a</math>, <math>b</math>, and <math>c</math> be pairwise relatively prime positive integers. Suppose one of these numbers is prime, and the other two are perfect squares. If <math>abc</math> has <math>15a</math> divisors and <math>a^{2}b^{2}c^{2}</math> has <math>15b</math> divisors, what is the least possible value of <math>a + b + c</math>? | ||
| − | + | <math>\textbf{(A)}~18\qquad\textbf{(B)}~44\qquad\textbf{(C)}~108\qquad\textbf{(D)}~141\qquad\textbf{(E)}~636</math> | |
| − | |||
| − | <math>\textbf{(A) } | ||
[[2024 AMC 10A Problems/Problem 22|Solution]] | [[2024 AMC 10A Problems/Problem 22|Solution]] | ||
==Problem 23== | ==Problem 23== | ||
| + | The figure below shows a dotted grid <math>8</math> cells wide and <math>3</math> cells tall consisting of <math>1^{\prime\prime} \times 1^{\prime\prime}</math> squares. Carl places <math>1</math>-inch toothpicks along some of the sides of the squares to create a closed loop that does not intersect itself. The numbers in the cells indicate the number of sides of that square that are to be covered by toothpicks, and any number of toothpicks are allowed if no number is written. In how many ways can Carl place the toothpicks? | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<asy> | <asy> | ||
size(6cm); | size(6cm); | ||
| Line 237: | Line 264: | ||
}}} | }}} | ||
</asy> | </asy> | ||
| − | <math>\textbf{(A) }130\qquad\textbf{(B) }144\qquad\textbf{(C) }146\qquad\textbf{(D) }162\qquad\textbf{(E) }196</math> | + | |
| + | <math>\textbf{(A)}~130\qquad\textbf{(B)}~144\qquad\textbf{(C)}~146\qquad\textbf{(D)}~162\qquad\textbf{(E)}~196</math> | ||
| + | |||
| + | [[2024 AMC 10A Problems/Problem 23|Solution]] | ||
| + | |||
| + | ==Problem 24== | ||
| + | There exists a unique two-digit prime number <math>p</math> such that both <math>4^{28} - 15</math> and <math>3^{28} - 20</math> are divisible by <math>p</math>. What is the sum of the digits of <math>p</math>? | ||
| + | |||
| + | <math>\textbf{(A)}~10\qquad\textbf{(B)}~11\qquad\textbf{(C)}~13\qquad\textbf{(D)}~14\qquad\textbf{(E)}~16</math> | ||
| + | |||
| + | [[2024 AMC 10A Problems/Problem 24|Solution]] | ||
| + | |||
| + | ==Problem 25== | ||
| + | In parallelogram <math>ABCD</math>, let <math>\omega</math> be the circle with diameter <math>\overline{AD}</math> and suppose <math>P</math> and <math>Q</math> are points on <math>\omega</math> such that both lines <math>BP</math> and <math>BQ</math> are tangent to <math>\omega</math>. If <math>BC = 8</math>, <math>BP = 3</math>, and line <math>PQ</math> bisects <math>\overline{CD}</math>, what is <math>AC^{2}</math>? | ||
| + | |||
| + | <math>\textbf{(A)}~180\qquad\textbf{(B)}~181\qquad\textbf{(C)}~182\qquad\textbf{(D)}~183\qquad\textbf{(E)}~184</math> | ||
[[2024 AMC 10A Problems/Problem 25|Solution]] | [[2024 AMC 10A Problems/Problem 25|Solution]] | ||
Revision as of 21:31, 20 March 2025
| 2024 AMC 10A (Answer Key) Printable versions: • AoPS Resources • PDF | ||
|
Instructions
| ||
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
Contents
[hide]- 1 Problem 1
- 2 Problem 2
- 3 Problem 3
- 4 Problem 4
- 5 Problem 5
- 6 Problem 6
- 7 Problem 7
- 8 Problem 8
- 9 Problem 9
- 10 Problem 10
- 11 Problem 11
- 12 Problem 12
- 13 Problem 13
- 14 Problem 14
- 15 Problem 15
- 16 Problem 16
- 17 Problem 17
- 18 Problem 18
- 19 Problem 19
- 20 Problem 20
- 21 Problem 21
- 22 Problem 22
- 23 Problem 23
- 24 Problem 24
- 25 Problem 25
- 26 See also
Problem 1
What is the value of ![]() ?
?
![]()
Problem 2
Define ![]() and
and ![]() for all real numbers
for all real numbers ![]() . What is the value of
. What is the value of ![]()
![]()
Problem 3
What is the sum of the digits of the smallest prime that can be written as a sum of ![]() distinct primes?
distinct primes?
![]()
Problem 4
A square and an isosceles triangle are joined along an edge to form a pentagon ![]() inches tall and
inches tall and ![]() inches wide, as shown below. What is the perimeter of the pentagon, in inches?
inches wide, as shown below. What is the perimeter of the pentagon, in inches?
![[asy] import graph; size(7cm); real labelscalefactor = 0.5; /* changes label-to-point distance */ pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ pen dotstyle = black; /* point style */ pen GGG = grey; draw((10, 0)--(0, 0)--(0, 10)--(10, 10)); draw((10, 0)--(10, 10), dashed); draw((10, 0)--(22, 5)--(10, 10)); draw((-1.5, 0)--(-1.5, 10), arrow = ArcArrow(SimpleHead), GGG); draw((-1.5, 10)--(-1.5, 0), arrow = ArcArrow(SimpleHead), GGG); draw((0, 11.5)--(22, 11.5), arrow = ArcArrow(SimpleHead), GGG); draw((22, 11.5)--(0, 11.5), arrow = ArcArrow(SimpleHead), GGG); label("$10$ in.", (-3.5, 5), GGG); label("$22$ in.", (11, 12.75), GGG); dot((0, 0)); dot((0, 10)); dot((10, 10)); dot((10, 0)); dot((22, 5)); [/asy]](http://latex.artofproblemsolving.com/e/b/1/eb1888f5cc06dc259137a47d906ed488b3dce141.png)
![]()
Problem 5
Andrea is taking a series of several exams. If Andrea earns ![]() points on her next exam, her average score will decrease by
points on her next exam, her average score will decrease by ![]() points. If she instead earns
points. If she instead earns ![]() points on her next exam, her average score will increase by
points on her next exam, her average score will increase by ![]() point. How many points should Andrea earn on her next exam to keep her average score constant?
point. How many points should Andrea earn on her next exam to keep her average score constant?
![]()
Problem 6
How many ordered pairs ![]() of positive integers exist such that
of positive integers exist such that ![]() is a factor of
is a factor of ![]() and
and ![]() is a factor of
is a factor of ![]() ?
?
![]()
Problem 7
Let ![]() be the midpoint of segment
be the midpoint of segment ![]() , and let
, and let ![]() lie on segment
lie on segment ![]() so that
so that ![]() and
and ![]() . What is the length of segment
. What is the length of segment ![]() ?
?
![]()
Problem 8
In how many ways can ![]() juniors and
juniors and ![]() seniors form
seniors form ![]() disjoint teams of
disjoint teams of ![]() people so
that each team has
people so
that each team has ![]() juniors and
juniors and ![]() seniors?
seniors?
![]()
Problem 9
Let ![]() be the least positive integer that is divisible by at least
be the least positive integer that is divisible by at least ![]() odd primes and at least
odd primes and at least ![]() perfect squares. What is the sum of the squares of the digits of
perfect squares. What is the sum of the squares of the digits of ![]() ?
?
![]()
Problem 10
Let ![]() be the kite formed by joining two right triangles with legs
be the kite formed by joining two right triangles with legs ![]() and
and ![]() along a common hypotenuse. Eight copies of
along a common hypotenuse. Eight copies of ![]() are used to form the polygon shown below. What is the area of triangle
are used to form the polygon shown below. What is the area of triangle ![]() ?
?
![]()
Problem 11
If ![]() and
and ![]() are real numbers satisfying
are real numbers satisfying ![]() and
and ![]() , what is the value of
, what is the value of ![]() ?
?
![]()
Problem 12
Square ![]() has side length
has side length ![]() and center
and center ![]() . Points
. Points ![]() and
and ![]() lie in the plane, and
lie in the plane, and ![]() is a rectangle. Suppose that exactly
is a rectangle. Suppose that exactly ![]() of the area of
of the area of ![]() lies inside square
lies inside square ![]() . What is the area of
. What is the area of ![]() ?
?
![]()
Problem 13
Aubrey raced his younger brother Blair. Aubrey runs at a faster constant speed than Blair, so Blair started the race ![]() feet ahead of Aubrey. Aubrey caught up to Blair after
feet ahead of Aubrey. Aubrey caught up to Blair after ![]() seconds, finishing the race
seconds, finishing the race ![]() feet ahead of Blair and
feet ahead of Blair and ![]() seconds earlier than Blair. How far did Aubrey run, in feet?
seconds earlier than Blair. How far did Aubrey run, in feet?
![]()
Problem 14
All of the rectangles in the figure below, which is drawn to scale, are similar to the enclosing rectangle. Each number represents the area of the rectangle. What is the length ![]() ?
?
![]()
Problem 15
Let ![]() be a subset of
be a subset of ![]() such that the following two conditions hold:
such that the following two conditions hold:
- If
 and
and  are distinct elements of
are distinct elements of  , then
, then  .
. - If
 and
and  are distinct odd elements of
are distinct odd elements of  , then
, then  .
.
What is the maximum possible number of elements in ![]() ?
?
![]()
Problem 16
In how many ways can the integers ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() be arranged in a line so that the following statement is true? If
be arranged in a line so that the following statement is true? If ![]() is not adjacent to
is not adjacent to ![]() , then
, then ![]() is not adjacent to
is not adjacent to ![]() .
.
![]()
Problem 17
The numbers, in order, of each row and the numbers, in order, of each column of a ![]() array of integers form an arithmetic progression of length
array of integers form an arithmetic progression of length ![]() . The numbers in positions
. The numbers in positions ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are
are ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , respectively. What number is in position
, respectively. What number is in position ![]() ?
? ![\[\begin{bmatrix}. & ? & . & . & . \\. & . & . & 48 & . \\ 12 & . & . & . & . \\ . & . & 16 & . & . \\ . & . & . & . & 0\end{bmatrix}\]](http://latex.artofproblemsolving.com/6/0/1/6018d11c73a8a522a8499fdd17c5570efca58713.png)
![]()
Problem 18
Points ![]() and
and ![]() lie on sides
lie on sides ![]() and
and ![]() , respectively, of parallelogram
, respectively, of parallelogram ![]() such that
such that ![]() . Suppose
. Suppose ![]() and
and ![]() , as shown. If
, as shown. If ![]() has perimeter
has perimeter ![]() , what is its area?
, what is its area?
![[asy] import olympiad; import graph; size(8cm); real labelscalefactor = 0.5; /* changes label-to-point distance */ pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ pen dotstyle = black; /* point style */ pair A = (0, 0), B = (15, 0), C = (12, -6 * sqrt(2)), D = (-3, -6 * sqrt(2)); pair X = (15 - 3 * 5/9, -6 * sqrt(2) * 5 / 9); pair Y = (0, -6 * sqrt(2)); dot(A); dot(B); dot(C); dot(D); dot(X); dot(Y); draw(A--B--C--D--cycle); draw(A--X); draw(A--Y); draw(rightanglemark(A,X,C,15)); draw(rightanglemark(A,Y,C,15)); label("$A$", A, N * 1.5); label("$B$", B, N * 1.5); label("$C$", C, S * 1.5); label("$D$", D, S * 1.5); label("$X$", X, E * 1.5); label("$Y$", Y, S * 1.5); label("$3$", midpoint(D--Y), S * 1.5); label("$5$", midpoint(B--X), E * 1.5); [/asy]](http://latex.artofproblemsolving.com/0/8/d/08d0af36b1e6ac10bc5e8096a8ba3421c0ea519d.png)
![]()
Problem 19
A bee is moving in three-dimensional space. A fair six-sided die with faces labeled ![]() , and
, and ![]() is rolled. Suppose the bee occupies the point
is rolled. Suppose the bee occupies the point ![]() . If the die shows
. If the die shows ![]() , then the bee moves to the point
, then the bee moves to the point ![]() and if the die shows
and if the die shows ![]() , then the bee moves to the point
, then the bee moves to the point ![]() . Analogous moves are made with the other four outcomes. Suppose the bee starts at the point
. Analogous moves are made with the other four outcomes. Suppose the bee starts at the point ![]() and the die is rolled four times. What is the probability that the bee traverses four distinct edges of some unit cube?
and the die is rolled four times. What is the probability that the bee traverses four distinct edges of some unit cube?
![]()
Problem 20
Point ![]() lies outside regular pentagon
lies outside regular pentagon ![]() so that
so that ![]() is an equilateral triangle, as shown below. What is the degree measure of acute angle
is an equilateral triangle, as shown below. What is the degree measure of acute angle ![]() ?
?
![[asy] import graph; size(7cm); real labelscalefactor = 0.75; /* changes label-to-point distance */ pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ pen dotstyle = black; /* point style */ real xmin = -1.089556028373145, xmax = 2.738320502950249, ymin = -1.3143096399343266, ymax = 1.2691431521185288; /* image dimensions */ pen qqwuqq = rgb(0,0.39215686274509803,0); filldraw(arc((1.9562952014676112,0),0.25,168,192)--(1.9562952014676112,0)--cycle, mediumgrey); /* draw figures */ draw((-0.8090169943749473,0.5877852522924731)--(0.30901699437494745,0.9510565162951535)); draw((0.30901699437494745,0.9510565162951535)--(1,0)); draw((1,0)--(0.3090169943749473,-0.9510565162951536)); draw((0.3090169943749473,-0.9510565162951536)--(-0.8090169943749475,-0.587785252292473)); draw((-0.8090169943749475,-0.587785252292473)--(-0.8090169943749473,0.5877852522924731)); draw((0.30901699437494745,0.9510565162951535)--(0.3090169943749473,-0.9510565162951536)); draw((0.3090169943749473,-0.9510565162951536)--(1.9562952014676112,0)); draw((1.9562952014676112,0)--(0.30901699437494745,0.9510565162951535)); draw((-0.8090169943749473,0.5877852522924731)--(1.9562952014676112,0), dashed); draw((1.9562952014676112,0)--(-0.8090169943749475,-0.587785252292473), dashed); /* dots and labels */ dot((1,0),linewidth(4pt) + dotstyle); label("$A$", (1.013592864312142,0), E * labelscalefactor); dot((0.30901699437494745,0.9510565162951535),linewidth(4pt) + dotstyle); label("$B$", (0.26,1), NE * labelscalefactor); dot((-0.8090169943749473,0.5877852522924731),linewidth(4pt) + dotstyle); label("$C$", (-0.82,0.64), NW * 0.25); dot((-0.8090169943749475,-0.587785252292473),linewidth(4pt) + dotstyle); label("$D$", (-0.82,-0.64), SW * 0.25); dot((0.3090169943749473,-0.9510565162951536),linewidth(4pt) + dotstyle); label("$E$", (0.26,-1), SE * labelscalefactor); dot((1.9562952014676112,0),linewidth(4pt) + dotstyle); label("$X$", (1.9705619971429902, 0), E * labelscalefactor); clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle); /* end of picture */ [/asy]](http://latex.artofproblemsolving.com/a/8/8/a885f409e123b4a6560ad0c31c863f12ac435565.png)
![]()
Problem 21
A fair six-sided die is repeatedly rolled until the same number is rolled twice in a row. What is the probability that the last number rolled is equal to the first number rolled?
![]()
Problem 22
Let ![]() ,
, ![]() , and
, and ![]() be pairwise relatively prime positive integers. Suppose one of these numbers is prime, and the other two are perfect squares. If
be pairwise relatively prime positive integers. Suppose one of these numbers is prime, and the other two are perfect squares. If ![]() has
has ![]() divisors and
divisors and ![]() has
has ![]() divisors, what is the least possible value of
divisors, what is the least possible value of ![]() ?
?
![]()
Problem 23
The figure below shows a dotted grid ![]() cells wide and
cells wide and ![]() cells tall consisting of
cells tall consisting of ![]() squares. Carl places
squares. Carl places ![]() -inch toothpicks along some of the sides of the squares to create a closed loop that does not intersect itself. The numbers in the cells indicate the number of sides of that square that are to be covered by toothpicks, and any number of toothpicks are allowed if no number is written. In how many ways can Carl place the toothpicks?
-inch toothpicks along some of the sides of the squares to create a closed loop that does not intersect itself. The numbers in the cells indicate the number of sides of that square that are to be covered by toothpicks, and any number of toothpicks are allowed if no number is written. In how many ways can Carl place the toothpicks?
![[asy] size(6cm); for (int i=0; i<9; ++i) { draw((i,0)--(i,3),dotted); } for (int i=0; i<4; ++i){ draw((0,i)--(8,i),dotted); } for (int i=0; i<8; ++i) { for (int j=0; j<3; ++j) { if (j==1) { label("1",(i+0.5,1.5)); }}} [/asy]](http://latex.artofproblemsolving.com/9/d/1/9d176dfd41e3e8e875c6b5d84fdb4f5e4f7d43a6.png)
![]()
Problem 24
There exists a unique two-digit prime number ![]() such that both
such that both ![]() and
and ![]() are divisible by
are divisible by ![]() . What is the sum of the digits of
. What is the sum of the digits of ![]() ?
?
![]()
Problem 25
In parallelogram ![]() , let
, let ![]() be the circle with diameter
be the circle with diameter ![]() and suppose
and suppose ![]() and
and ![]() are points on
are points on ![]() such that both lines
such that both lines ![]() and
and ![]() are tangent to
are tangent to ![]() . If
. If ![]() ,
, ![]() , and line
, and line ![]() bisects
bisects ![]() , what is
, what is ![]() ?
?
![]()
See also
| 2024 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by 2023 AMC 10B Problems |
Followed by 2024 AMC 10B Problems | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||