Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2024 AMC 12B Problems/Problem 12"

(→‎Problem)
(→‎Solution 2 (shoelace theorem))
Line 33: Line 33:
 
We have the vertices:
 
We have the vertices:
  
−
1.<math> 0 </math> at<math>(0, 0)</math>
+
<math> 0 </math> at<math>(0, 0)</math> , <math> z </math> at<math>(2\cos \theta, 2\sin \theta)</math> , <math> z^2 </math> at<math>(4\cos 2\theta, 4\sin 2\theta)</math> , <math> z^3 </math> at<math>(8\cos 3\theta, 8\sin 3\theta)</math>
−
 
 
−
2.<math> z </math> at<math>(2\cos \theta, 2\sin \theta)</math>
 
−
 
 
−
3.<math> z^2 </math> at<math>(4\cos 2\theta, 4\sin 2\theta)</math>
 
−
 
 
−
4.<math> z^3 </math> at<math>(8\cos 3\theta, 8\sin 3\theta)</math>
 
  
 
The Shoelace formula for the area is:
 
The Shoelace formula for the area is:
 
<cmath>
 
<cmath>
−
\text{Area} = \frac{1}{2} \left| x_1 y_2 + x_2 y_3 + x_3 y_4 + x_4 y_1 - (y_1 x_2 + y_2 x_3 + y_3 x_4 + y_4 x_1) \right|.
+
= \frac{1}{2} \left| x_1 y_2 + x_2 y_3 + x_3 y_4 + x_4 y_1 - (y_1 x_2 + y_2 x_3 + y_3 x_4 + y_4 x_1) \right|.
 
</cmath>
 
</cmath>
 
<cmath>
 
<cmath>
−
\text{Area} = \frac{1}{2} \left| 0 + 2\cos \theta \cdot 4\sin 2\theta + 4\cos 2\theta \cdot 8\sin 3\theta - (2\sin \theta \cdot 4\cos 2\theta + 4\sin 2\theta \cdot 8\cos 3\theta) \right|.
+
= \frac{1}{2} \left| 0 + 2\cos \theta \cdot 4\sin 2\theta + 4\cos 2\theta \cdot 8\sin 3\theta - (2\sin \theta \cdot 4\cos 2\theta + 4\sin 2\theta \cdot 8\cos 3\theta) \right|.
 
</cmath>
 
</cmath>
 
<cmath>
 
<cmath>
−
\text{Area} = \frac{1}{2} \left| 8\cos \theta \sin 2\theta + 32\cos 2\theta \sin 3\theta - 8\sin \theta \cos 2\theta - 32\sin 2\theta \cos 3\theta \right|.
+
= \frac{1}{2} \left| 8\cos \theta \sin 2\theta + 32\cos 2\theta \sin 3\theta - 8\sin \theta \cos 2\theta - 32\sin 2\theta \cos 3\theta \right|
 
</cmath>
 
</cmath>
 
<cmath>
 
<cmath>
−
\text{Area} = \frac{1}{2} \left|8\cos \theta \sin 2\theta - 8\sin \theta \cos 2\theta)  + (32\cos 2\theta \sin 3\theta - 32\sin 2\theta \cos 3\theta))  \right|.</cmath>
+
= \frac{1}{2} \left|8\cos \theta \sin 2\theta - 8\sin \theta \cos 2\theta)  + (32\cos 2\theta \sin 3\theta - 32\sin 2\theta \cos 3\theta) \right|</cmath>
 +
<cmath>
 +
= \frac{1}{2} \left|8\sin(2\theta - \theta)  + 32\sin(2\theta - \theta)  \right|
 +
</cmath>
 
<cmath>
 
<cmath>
−
\text{Area} = \frac{1}{2} \left|8\sin(2\theta - \theta)  + (32\sin(2\theta - \theta)  \right|.</cmath>
+
= \frac{1}{2} \left| 8\sin \theta + 32\sin \theta \right|  
−
<cmath>
+
</cmath>
−
\text{Area} = \frac{1}{2} \left| 8\sin \theta + 32\sin \theta \right| = \frac{1}{2} \left| 40\sin \theta \right|.
+
<cmath>= \frac{1}{2} \left| 40\sin \theta \right|
 
</cmath>
 
</cmath>
 
Given that the area is 15:
 
Given that the area is 15:
Line 65: Line 62:
 
20|\sin \theta| = 15 \implies |\sin \theta| = \frac{3}{4}.
 
20|\sin \theta| = 15 \implies |\sin \theta| = \frac{3}{4}.
 
</cmath>
 
</cmath>
−
Since<math> \theta </math> corresponds to a complex number<math> z </math> with a positive imaginary part, we have:
+
Since <math> \theta </math> corresponds to a complex number <math> z </math> with a positive imaginary part, we have:
  
 
<cmath>
 
<cmath>

Revision as of 22:10, 14 November 2024

Problem

Suppose $z$ is a complex number with positive imaginary part, with real part greater than $1$, and with $|z| = 2$. In the complex plane, the four points $0$, $z$, $z^{2}$, and $z^{3}$ are the vertices of a quadrilateral with area $15$. What is the imaginary part of $z$?

$\textbf{(A) }\frac{3}{4}\qquad\textbf{(B) }1\qquad\textbf{(C) }\frac{4}{3}\qquad\textbf{(D) }\frac{3}{2}\qquad\textbf{(E) }\frac{5}{3}$

Diagram

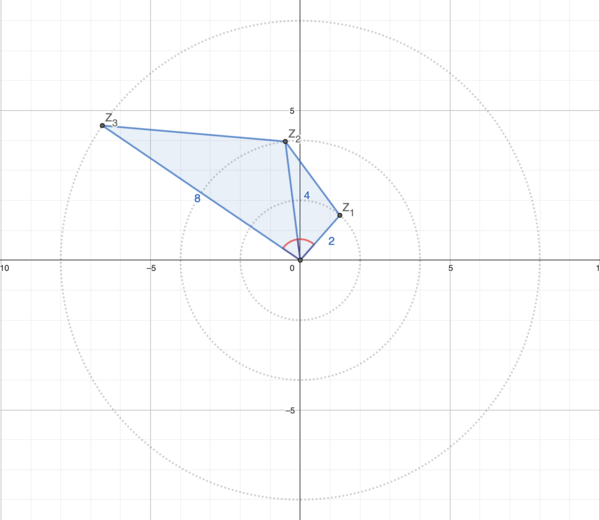
2024 12B Q12.png

Solution 1 (similar triangles)

By making a rough estimate of where $z$, $z^2$, and $z^3$ are on the complex plane, we can draw a pretty accurate diagram (like above.)

Here, points $Z_1$, $Z_2$, and $Z_3$ lie at the coordinates of $z$, $z^2$, and $z^3$ respectively, and $O$ is the origin.

We're given $|z|=2$, so $|z^2|=|z|^2=4$ and $|z^3|=|z|^3 = 8$. This gives us $OZ_1=2$, $OZ_2=4$, and $OZ_3=8$.

Additionally, we know that $\angle{Z_1OZ_2}\cong\angle{Z_2OZ_3}$ (since every power of $z$ rotates around the origin by the same angle.) We set these angles equal to $\theta$.

This gives us enough info to say that $\triangle{OZ_1Z_2}\sim\triangle{OZ_2Z_3}$ by SAS similarity (since $\frac{OZ_2}{OZ_1}=\frac{OZ_3}{OZ_2}=2$.)

It follows that $[OZ_1Z_2Z_3]=[OZ_1Z_2]+[OZ_2Z_3]=[OZ_1Z_2]+2^2[OZ_1Z_2]=5[OZ_1Z_2]$ as the ratio of side lengths of the two triangles is 2 to 1.

This means $5[OZ_1Z_2]=15$ or $[OZ_1Z_2]=3$ as we were given $[OZ_1Z_2Z_3]=15$.

Using $A=\frac{ab\sin(C)}{2}$, we get that $[OZ_1Z_2]=\frac{2\cdot4\cdot \sin(\theta)}{2}=4\sin(\theta)$, so $4\sin(\theta)=3$, giving $\sin(\theta)=\frac{3}{4}$.

Thus, $\text{Im}(z)=|z|\sin(\theta)=2(\frac{3}{4})=\boxed{\textbf{(D) }\frac{3}{2}}$.

~nm1728

Solution 2 (shoelace theorem)

We have the vertices:

$0$ at$(0, 0)$ , $z$ at$(2\cos \theta, 2\sin \theta)$ , $z^2$ at$(4\cos 2\theta, 4\sin 2\theta)$ , $z^3$ at$(8\cos 3\theta, 8\sin 3\theta)$

The Shoelace formula for the area is: \[= \frac{1}{2} \left| x_1 y_2 + x_2 y_3 + x_3 y_4 + x_4 y_1 - (y_1 x_2 + y_2 x_3 + y_3 x_4 + y_4 x_1) \right|.\] \[= \frac{1}{2} \left| 0 + 2\cos \theta \cdot 4\sin 2\theta + 4\cos 2\theta \cdot 8\sin 3\theta - (2\sin \theta \cdot 4\cos 2\theta + 4\sin 2\theta \cdot 8\cos 3\theta) \right|.\] \[= \frac{1}{2} \left| 8\cos \theta \sin 2\theta + 32\cos 2\theta \sin 3\theta - 8\sin \theta \cos 2\theta - 32\sin 2\theta \cos 3\theta \right|\] \[= \frac{1}{2} \left|8\cos \theta \sin 2\theta - 8\sin \theta \cos 2\theta) + (32\cos 2\theta \sin 3\theta - 32\sin 2\theta \cos 3\theta) \right|\] \[= \frac{1}{2} \left|8\sin(2\theta - \theta) + 32\sin(2\theta - \theta) \right|\] \[= \frac{1}{2} \left| 8\sin \theta + 32\sin \theta \right|\] \[= \frac{1}{2} \left| 40\sin \theta \right|\] Given that the area is 15: \[\frac{1}{2} \left| 40\sin \theta \right| = 15.\] \[20|\sin \theta| = 15 \implies |\sin \theta| = \frac{3}{4}.\] Since $\theta$ corresponds to a complex number $z$ with a positive imaginary part, we have:

\[\sin \theta = \frac{3}{4}.\] \[\text{Imaginary part} = 2\sin \theta = 2 \times \frac{3}{4} = \boxed{\textbf{(D) }\frac{3}{2}}.\]

~luckuso

Solution 3 (No Trig)

Let $z = a + bi$, so $z^2 = a^2 + 2abi - b^2$ and $z^3 = a^3 + 3a^2 bi - 3ab^2 - b^3 i$. Therefore, converting $0, z, z^2, z^3$ from complex coordinates to Cartesian coordinates gives us the following.

\[(0, 0)\]

\[(a, b)\]

\[(a^2 - b^2, 2ab)\]

\[(a^3 - 3ab^2, 3a^2 b - b^3)\]

The Shoelace Theorem tells us that the area is

\[\frac{1}{2} \Bigg| \Big[ (0)(b) + (a)(2ab) + (a^2 - b^2)(3a^2 b - b^3) + (a^3 - 3ab^2)(0) \Big] - \Big[ (0)(a) + (b)(a^2 - b^2) + (2ab)(a^3 - 3ab^2) + (3a^2 b - b^3)(0) \Big] \Bigg|\]

\[= \frac{1}{2} \Bigg| \Big[ (0) + (2a^2 b) + (3a^4 b - a^2 b^3 - 3a^2 b^3 + b^5) + (0) \Big] - \Big[ (0) + (a^2 b - b^3) + (2a^4 b - 6a^2 b^3) + (0) \Big] \Bigg|\]

\[= \frac{1}{2} \Big| [3a^4 b - 4a^2 b^3 + b^5 + 2a^2 b] - [2a^4 b - 6a^2 b^3 + a^2 b - b^3] \Big|\]

\[= \frac{1}{2} | a^4 b + 2a^2 b^3 + b^5 + a^2 b + b^3 |.\]

We know that $|z| = |a + bi| = \sqrt{a^2 + b^2} = 2$, so $a^2 = 4 - b^2$. Substituting this gives us this:

\[\frac{1}{2} \Big| (4 - b^2)^2 b + 2(4 - b^2)b^3 + b^5 + (4 - b^2)b + b^3 \Big|\]

\[= \frac{1}{2} \Big| (16b - 8b^3 + b^5) + (8b^3 - 2b^5) + b^5 + (4b - b^3) + b^3 \Big|\]

\[= \frac{1}{2} | 0b^5 + 0b^3 + 20b|\]

\[= 15.\]

In other words,

\[|10b| = 15\]

\[b = \textbf{(D) } \frac{3}{2}.\]

See also

2024 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 11 		Followed by
Problem 13
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2024_AMC_12B_Problems/Problem_12&oldid=234215"