Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Japanese Theorem"

(added deletion request)
(Undo revision 230989 by Charking (talk))
(Tag: Undo)
Line 1: Line 1:
−
{{delete|not a real theorem}}
+
The '''Japanese theorem''' exists for both [[Cyclic_quadrilateral | cyclic quadrilaterals]] and [[Cyclic | cyclic polygons]].
 +
 
 +
==Japanese theorem for cyclic quadrilaterals==
 +
 
 +
 
 +
====Definition====
 +
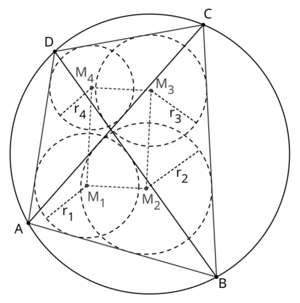
The '''Japanese theorem for cyclic quadrilaterals''' states that for a cyclic quadrilateral <math>ABCD</math> and [[Incenter | incenters]] <math>M_1</math>, <math>M_2</math>, <math>M_3</math>, <math>M_4</math> of triangles <math>\triangle ABD</math>, <math>\triangle ABC</math>, <math>\triangle BCD</math>, <math>\triangle ACD</math> the quadrilateral <math>M_1M_2M_3M_4</math> is a [[Rectangle | rectangle]].
 +
 
 +
 
 +
[[File:japanese_theorem_quadrilaterals.png|300px|thumb|left]]
 +
 
 +
====Proof====
 +
From <math>\triangle ABC</math>, we can see that
 +
 
 +
<math>\angle BM_2C = 90^{\circ} + \frac{1}{2} \angle CAB</math>
 +
 
 +
Similarly, from <math>\triangle BCD</math> we have
 +
 
 +
<math>\angle BM_3C = 90^{\circ} + \frac{1}{2} \angle CDB</math>
 +
 
 +
Since <math>ABCD</math> is cyclic, therefore <math>\angle CDB = \angle CAB</math>, which means that
 +
 
 +
<math>\angle BM_2C = \angle BM_3C</math>
 +
 
 +
From this, it follows that <math>BM_2M_3C</math> is cyclic. This means that
 +
 
 +
<math>\angle BCM_3 + \angle BM_2M_3 = 180^{\circ}</math>
 +
 
 +
By symmetry, we can also derive
 +
 
 +
<math>\angle BAM_1 + \angle BM_2M_1 = 180^{\circ}</math>
 +
 
 +
Adding these equations up, we get
 +
 
 +
<math>\angle BAM_1 + \angle BCM_3 + \angle BM_2M_1 + \angle BM_2M_3 = 360^{\circ}</math>
 +
 
 +
<math>\Rightarrow \angle BM_2M_1 + \angle BM_2M_3 = 360^{\circ} - \angle BAM_1 - \angle BCM_3 = 360^{\circ} - \frac{1}{2} \left(\angle CAB + \angle CDB \right)</math>
 +
 
 +
Which implies
 +
 
 +
<math>M_1M_2M_3 = 90^{\circ}</math>
 +
 
 +
And other angles similarly.
 +
 
 +
<math>Q.E.D.</math>
 +
 
 +
 
 +
==Japanese theorem for cyclic polygons==
 +
 
 +
 
 +
====Definition====
 +
The '''Japanese theorem for cyclic polygons''' states that for any triangulated cyclic polygon, the sum of the [[Inradius || inradii]] of the triangles is constant.

Revision as of 13:42, 31 March 2025

The Japanese theorem exists for both cyclic quadrilaterals and cyclic polygons.

Japanese theorem for cyclic quadrilaterals

Definition

The Japanese theorem for cyclic quadrilaterals states that for a cyclic quadrilateral $ABCD$ and incenters $M_1$, $M_2$, $M_3$, $M_4$ of triangles $\triangle ABD$, $\triangle ABC$, $\triangle BCD$, $\triangle ACD$ the quadrilateral $M_1M_2M_3M_4$ is a rectangle.


Japanese theorem quadrilaterals.png

Proof

From $\triangle ABC$, we can see that

$\angle BM_2C = 90^{\circ} + \frac{1}{2} \angle CAB$

Similarly, from $\triangle BCD$ we have

$\angle BM_3C = 90^{\circ} + \frac{1}{2} \angle CDB$

Since $ABCD$ is cyclic, therefore $\angle CDB = \angle CAB$, which means that

$\angle BM_2C = \angle BM_3C$

From this, it follows that $BM_2M_3C$ is cyclic. This means that

$\angle BCM_3 + \angle BM_2M_3 = 180^{\circ}$

By symmetry, we can also derive

$\angle BAM_1 + \angle BM_2M_1 = 180^{\circ}$

Adding these equations up, we get

$\angle BAM_1 + \angle BCM_3 + \angle BM_2M_1 + \angle BM_2M_3 = 360^{\circ}$

$\Rightarrow \angle BM_2M_1 + \angle BM_2M_3 = 360^{\circ} - \angle BAM_1 - \angle BCM_3 = 360^{\circ} - \frac{1}{2} \left(\angle CAB + \angle CDB \right)$

Which implies

$M_1M_2M_3 = 90^{\circ}$

And other angles similarly.

$Q.E.D.$


Japanese theorem for cyclic polygons

Definition

The Japanese theorem for cyclic polygons states that for any triangulated cyclic polygon, the sum of the | inradii of the triangles is constant.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Japanese_Theorem&oldid=246294"