Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Simson line"

(→‎Baler line 🗿🗿 (main))
(Formatting)
 
Line 1: Line 1:
−
In [[geometry]], given a [[triangle]] ABC and a point P on its [[circumcircle]], the three closest points to P on lines AB, AC, and BC are [[collinear]].
+
In [[geometry]], given a [[triangle]] ABC and a point P on its [[circumcircle]], the three closest points to P on lines AB, AC, and BC are [[collinear]] and form a '''Simson line'''.
 +
 
 
[[File:Simsonline.png]]
 
[[File:Simsonline.png]]
  
−
== Simson Line (main)==
+
== Definition ==
 +
 
 +
[[File:Simson line.png|270px|right]]
 +
[[File:Simson line inverse.png|270px|right]]
 
Let a triangle <math>\triangle ABC</math> and a point <math>P</math> be given.
 
Let a triangle <math>\triangle ABC</math> and a point <math>P</math> be given.
  
Line 9: Line 13:
 
Then points  <math>D, E,</math> and <math>F</math> are collinear iff the point <math>P</math> lies on circumcircle of <math>\triangle ABC.</math>
 
Then points  <math>D, E,</math> and <math>F</math> are collinear iff the point <math>P</math> lies on circumcircle of <math>\triangle ABC.</math>
  
−
<i><b>Proof</b></i>
+
=== Proof of existence ===
  
 
Let the point <math>P</math> be on the circumcircle of <math>\triangle ABC.</math>
 
Let the point <math>P</math> be on the circumcircle of <math>\triangle ABC.</math>
Line 39: Line 43:
 
<math>ACBP</math> is cyclis as desired.
 
<math>ACBP</math> is cyclis as desired.
  
−
'''vladimir.shelomovskii@gmail.com, vvsss'''
+
== Simson line of a complete quadrilateral ==
  
−
==Simson line of a complete quadrilateral==
 
 
[[File:Simson complite.png|430px|right]]
 
[[File:Simson complite.png|430px|right]]
 
Let four lines made four triangles of a complete quadrilateral. In the diagram these are <math>\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.</math>  
 
Let four lines made four triangles of a complete quadrilateral. In the diagram these are <math>\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.</math>  
Line 51: Line 54:
 
Prove that points <math>K,L, N,</math> and <math>G</math> are collinear.  
 
Prove that points <math>K,L, N,</math> and <math>G</math> are collinear.  
  
−
<i><b>Proof</b></i>
+
=== Proof ===
  
 
Let <math>\Omega</math> be the circumcircle of <math>\triangle ABC, \omega</math> be the circumcircle of <math>\triangle CEF.</math> Then <math>M = \Omega \cap \omega.</math>
 
Let <math>\Omega</math> be the circumcircle of <math>\triangle ABC, \omega</math> be the circumcircle of <math>\triangle CEF.</math> Then <math>M = \Omega \cap \omega.</math>
Line 61: Line 64:
 
Therefore points <math>K, L, N,</math> and <math>G</math> are collinear, as desired.
 
Therefore points <math>K, L, N,</math> and <math>G</math> are collinear, as desired.
  
−
*[[Miquel's point]]
+
== Problems ==
−
*[[Steiner line]]
 
−
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
  
−
==Problem==
 
 
[[File:Problem on Simson line.png |400px|right]]
 
[[File:Problem on Simson line.png |400px|right]]
  
−
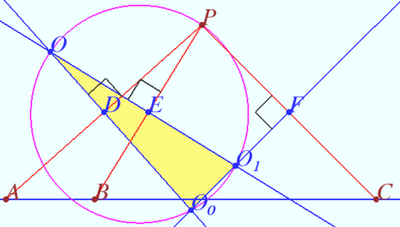
Let the points <math>A, B,</math> and <math>C</math> be collinear and the point <math>P \notin AB.</math>
+
*Let the points <math>A, B,</math> and <math>C</math> be collinear and the point <math>P \notin AB</math>. Let <math>O,O_0,</math> and <math>O_1</math> be the circumcenters of triangles <math>\triangle ABP, \triangle ACP,</math> and <math>\triangle BCP</math>. Prove that <math>P</math> lies on circumcircle of <math>\triangle OO_0O_1</math>.
  
−
Let <math>O,O_0,</math> and <math>O_1</math> be the circumcenters of triangles <math>\triangle ABP, \triangle ACP,</math> and <math>\triangle BCP.</math>
+
** Solution
 +
: Let <math>D, E,</math> and <math>F</math> be the midpoints of segments <math>AB, AC,</math> and <math>BC,</math> respectively. Then points  <math>D, E,</math> and <math>F</math> are collinear <math>(DE||AB, EF||DC).</math>
 +
<cmath>PD \perp OO_0, PE \perp OO_1, PF \perp O_0O_1 \implies</cmath>
 +
:<math>DEF</math> is Simson line of <math>\triangle OO_0O_1 \implies P</math> lies on circumcircle of <math>\triangle OO_0O_1</math> as desired.
  
−
Prove that <math>P</math> lies on circumcircle of <math>\triangle OO_0O_1.</math>
+
== See Also ==
−
 
+
*[[Miquel's point]]
−
<i><b>Proof</b></i>
+
*[[Steiner line]]
 +
*[[Euler line]]
  
−
Let <math>D, E,</math> and <math>F</math> be the midpoints of segments <math>AB, AC,</math> and <math>BC,</math> respectively.
 
  
−
Then points  <math>D, E,</math> and <math>F</math> are collinear <math>(DE||AB, EF||DC).</math>
+
{{stub}}
−
 
 
−
<math>PD \perp OO_0, PE \perp OO_1, PF \perp O_0O_1 \implies</math>
 
−
<math>DEF</math> is Simson line of <math>\triangle OO_0O_1 \implies P</math> lies on circumcircle of <math>\triangle OO_0O_1</math> as desired.
 
−
*[[Euler line]]
 
−
'''vladimir.shelomovskii@gmail.com, vvsss'''
 

Latest revision as of 18:48, 18 April 2025

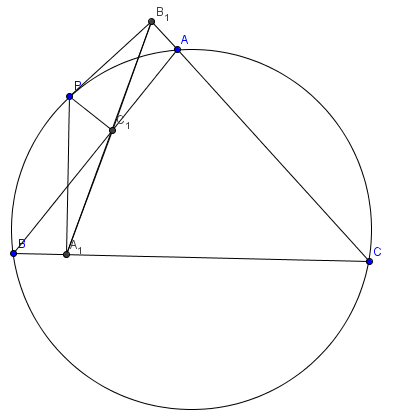
In geometry, given a triangle ABC and a point P on its circumcircle, the three closest points to P on lines AB, AC, and BC are collinear and form a Simson line.

Simsonline.png

Definition

Simson line.png
Simson line inverse.png

Let a triangle $\triangle ABC$ and a point $P$ be given.

Let $D, E,$ and $F$ be the foots of the perpendiculars dropped from P to lines AB, AC, and BC, respectively.

Then points $D, E,$ and $F$ are collinear iff the point $P$ lies on circumcircle of $\triangle ABC.$

Proof of existence

Let the point $P$ be on the circumcircle of $\triangle ABC.$

$\angle BFP = \angle BDP = 90^\circ \implies$

$BPDF$ is cyclic $\implies \angle PDF = 180^\circ – \angle CBP.$

$\angle ADP = \angle AEP = 90^\circ \implies$

$AEPD$ is cyclic $\implies \angle PDE = \angle PAE.$

$ACBP$ is cyclic $\implies \angle PBC = \angle PAE \implies \angle PDF + \angle PDE = 180^\circ$

$\implies D, E,$ and $F$ are collinear as desired.

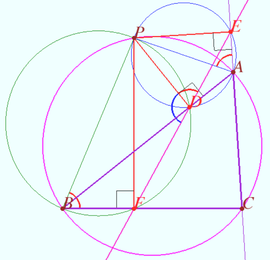
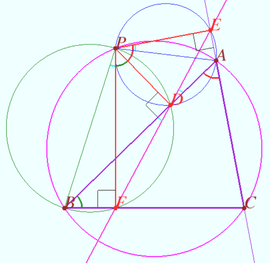
Proof

Let the points $D, E,$ and $F$ be collinear.

$AEPD$ is cyclic $\implies \angle APE = \angle ADE, \angle DPE = \angle BAC.$

$BFDP$ is cyclic $\implies \angle BPF = \angle BDF, \angle DPF = \angle ABC.$

$\angle ADE = \angle BDF \implies \angle BPA = \angle EPF$

$= \angle BAC + \angle ABC = 180^\circ – \angle ACB \implies$

$ACBP$ is cyclis as desired.

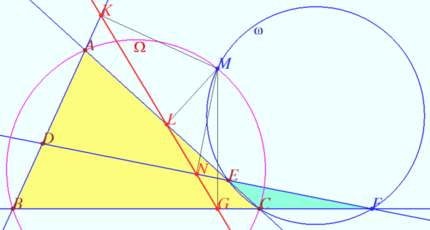
Simson line of a complete quadrilateral

Simson complite.png

Let four lines made four triangles of a complete quadrilateral. In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$

Let $M$ be the Miquel point of a complete quadrilateral.

Let $K, L, N,$ and $G$ be the foots of the perpendiculars dropped from $M$ to lines $AB, AC, EF,$ and $BC,$ respectively.

Prove that points $K,L, N,$ and $G$ are collinear.

Proof

Let $\Omega$ be the circumcircle of $\triangle ABC, \omega$ be the circumcircle of $\triangle CEF.$ Then $M = \Omega \cap \omega.$

Points $K, L,$ and $G$ are collinear as Simson line of $\triangle ABC.$

Points $L, N,$ and $G$ are collinear as Simson line of $\triangle CEF.$

Therefore points $K, L, N,$ and $G$ are collinear, as desired.

Problems

Problem on Simson line.png
  • Let the points $A, B,$ and $C$ be collinear and the point $P \notin AB$. Let $O,O_0,$ and $O_1$ be the circumcenters of triangles $\triangle ABP, \triangle ACP,$ and $\triangle BCP$. Prove that $P$ lies on circumcircle of $\triangle OO_0O_1$.
    • Solution
Let $D, E,$ and $F$ be the midpoints of segments $AB, AC,$ and $BC,$ respectively. Then points $D, E,$ and $F$ are collinear $(DE||AB, EF||DC).$

\[PD \perp OO_0, PE \perp OO_1, PF \perp O_0O_1 \implies\]

$DEF$ is Simson line of $\triangle OO_0O_1 \implies P$ lies on circumcircle of $\triangle OO_0O_1$ as desired.

See Also


This article is a stub. Help us out by expanding it.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Simson_line&oldid=246924"