Difference between revisions of "Steiner line"
Sknsdkvnkdvf (talk | contribs) (→Steiner line) |
(Formatting) (Tag: Undo) |
||
| Line 1: | Line 1: | ||
| − | == | + | A '''Steiner line''' is a line in [[geometry]]. |
| + | |||
| + | == Definition == | ||
| + | |||
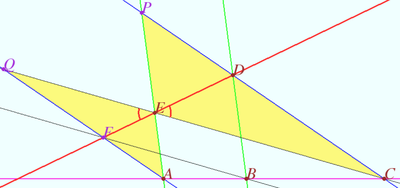
[[File:Steiner and Simson lines.png|500px|right]] | [[File:Steiner and Simson lines.png|500px|right]] | ||
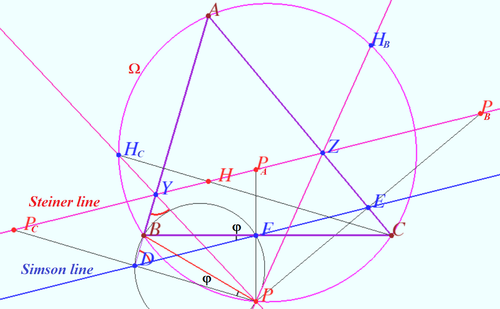
Let <math>ABC</math> be a triangle with orthocenter <math>H. P</math> is a point on the circumcircle <math>\Omega</math> of <math>\triangle ABC.</math> | Let <math>ABC</math> be a triangle with orthocenter <math>H. P</math> is a point on the circumcircle <math>\Omega</math> of <math>\triangle ABC.</math> | ||
| Line 5: | Line 8: | ||
Let <math>P_A, P_B, </math> and <math>P_C</math> be the reflections of <math>P</math> in three lines which contains edges <math>BC, AC,</math> and <math>AB,</math> respectively. | Let <math>P_A, P_B, </math> and <math>P_C</math> be the reflections of <math>P</math> in three lines which contains edges <math>BC, AC,</math> and <math>AB,</math> respectively. | ||
| − | + | <math>P_A, P_B, P_C,</math> and <math>H</math> are collinear. Respective line is known as the Steiner line of point <math>P</math> with respect to <math>\triangle ABC.</math> | |
| − | + | === Proof === | |
Let <math>D, E,</math> and <math>F</math> be the foots of the perpendiculars dropped from <math>P</math> to lines <math>AB, AC,</math> and <math>BC,</math> respectively. | Let <math>D, E,</math> and <math>F</math> be the foots of the perpendiculars dropped from <math>P</math> to lines <math>AB, AC,</math> and <math>BC,</math> respectively. | ||
| Line 29: | Line 32: | ||
According the Collins Claim <math>YZ</math> is <math>H-line,</math> therefore <math>H \in P_AP_B.</math> | According the Collins Claim <math>YZ</math> is <math>H-line,</math> therefore <math>H \in P_AP_B.</math> | ||
| − | |||
| − | |||
==Collings Clime== | ==Collings Clime== | ||
| Line 40: | Line 41: | ||
Prove that lines <math>l_A, l_B,</math> and <math>l_C</math> are concurrent and the point of concurrence lies on <math>\Omega.</math> | Prove that lines <math>l_A, l_B,</math> and <math>l_C</math> are concurrent and the point of concurrence lies on <math>\Omega.</math> | ||
| − | + | === Proof === | |
Let <math>D, E,</math> and <math>F</math> be the crosspoints of <math>H–line</math> with <math>AB, AC,</math> and <math>BC,</math> respectively. | Let <math>D, E,</math> and <math>F</math> be the crosspoints of <math>H–line</math> with <math>AB, AC,</math> and <math>BC,</math> respectively. | ||
| Line 57: | Line 58: | ||
Usually the point <math>P</math> is called the anti-Steiner point of the <math>H-line</math> with respect to <math>\triangle ABC.</math> | Usually the point <math>P</math> is called the anti-Steiner point of the <math>H-line</math> with respect to <math>\triangle ABC.</math> | ||
| − | |||
| − | ==Ortholine== | + | == Ortholine == |
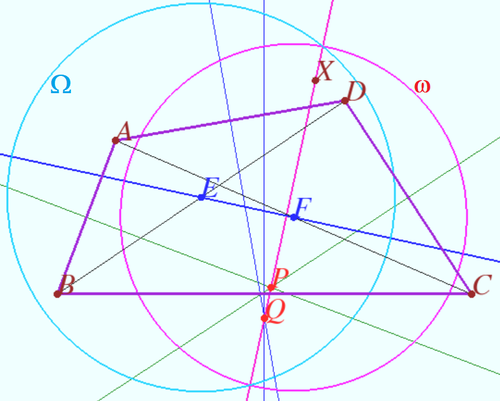
[[File:Ortholine.png|400px|right]] | [[File:Ortholine.png|400px|right]] | ||
Let four lines made four triangles of a complete quadrilateral. | Let four lines made four triangles of a complete quadrilateral. | ||
| Line 69: | Line 69: | ||
Prove that points <math>H, H_A, H_B,</math> and <math>H_C</math> are collinear. | Prove that points <math>H, H_A, H_B,</math> and <math>H_C</math> are collinear. | ||
| − | + | === Proof === | |
Let <math>M</math> be Miquel point of a complete quadrilateral. | Let <math>M</math> be Miquel point of a complete quadrilateral. | ||
| Line 77: | Line 77: | ||
Using homothety centered at <math>M</math> with ratio <math>2</math> we get <math>4</math> coinciding Stainer lines which contain points <math>H, H_A, H_B,</math> and <math>H_C</math>. | Using homothety centered at <math>M</math> with ratio <math>2</math> we get <math>4</math> coinciding Stainer lines which contain points <math>H, H_A, H_B,</math> and <math>H_C</math>. | ||
| − | + | === Proof 2 === | |
| − | |||
| − | |||
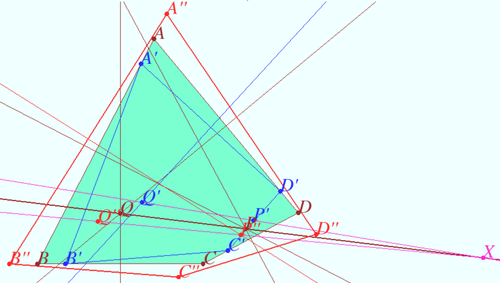
[[File:Steiner 2.png|400px|right]] | [[File:Steiner 2.png|400px|right]] | ||
<math>AH_A \perp DE, CH_C \perp EF \implies AH_A ||CH_C,</math> | <math>AH_A \perp DE, CH_C \perp EF \implies AH_A ||CH_C,</math> | ||
| Line 115: | Line 113: | ||
The segments <math>EF</math> and <math>ED</math> are corresponding segments in similar triangles. | The segments <math>EF</math> and <math>ED</math> are corresponding segments in similar triangles. | ||
Therefore <math>\angle CED = \angle QEF \implies D, E,</math> and <math>F</math> are collinear. | Therefore <math>\angle CED = \angle QEF \implies D, E,</math> and <math>F</math> are collinear. | ||
| − | |||
| − | |||
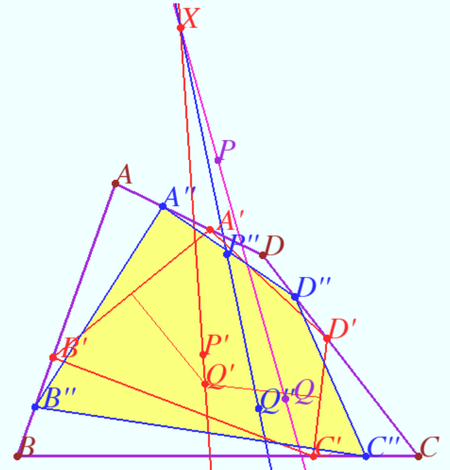
==Shatunov-Tokarev line== | ==Shatunov-Tokarev line== | ||
| Line 157: | Line 153: | ||
Of course, it is parallel to Simson line. | Of course, it is parallel to Simson line. | ||
*[[Complete Quadrilateral]] | *[[Complete Quadrilateral]] | ||
| − | |||
==Shatunov-Tokarev concurrent lines== | ==Shatunov-Tokarev concurrent lines== | ||
| Line 183: | Line 178: | ||
We made simple calculations and get <math>XA''^2 + XC''^2 = XB''^2 + XD''^2,</math> therefore point <math>X</math> lies on <math>P''Q''</math> as desired. | We made simple calculations and get <math>XA''^2 + XC''^2 = XB''^2 + XD''^2,</math> therefore point <math>X</math> lies on <math>P''Q''</math> as desired. | ||
| − | |||
==Shatunov point== | ==Shatunov point== | ||
| Line 212: | Line 206: | ||
We made simple calculations and get <math>|XA''|^2 + |XC''|^2 = |XB''|^2 + |XD''|^2,</math> therefore point <math>X</math> lies on <math>P''Q''</math> as desired. | We made simple calculations and get <math>|XA''|^2 + |XC''|^2 = |XB''|^2 + |XD''|^2,</math> therefore point <math>X</math> lies on <math>P''Q''</math> as desired. | ||
| − | |||
==Shatunov chain== | ==Shatunov chain== | ||
| Line 232: | Line 225: | ||
The claim follows from the fact that there are <math>4^2 = 16</math> combinations of quadrilateral vertices, and these 16 quadrilaterals are divided into pairs whose points of intersection with the line <math>PQ</math> coincide. | The claim follows from the fact that there are <math>4^2 = 16</math> combinations of quadrilateral vertices, and these 16 quadrilaterals are divided into pairs whose points of intersection with the line <math>PQ</math> coincide. | ||
| − | ' | + | == See Also == |
| + | |||
| + | *[[Miquel's point]] | ||
| + | *[[Simson line]] | ||
| + | *[[Complete Quadrilateral]] | ||
| + | |||
| + | {{stub}} | ||
Latest revision as of 18:52, 18 April 2025
A Steiner line is a line in geometry.
Contents
[hide]Definition
Let ![]() be a triangle with orthocenter
be a triangle with orthocenter ![]() is a point on the circumcircle
is a point on the circumcircle ![]() of
of ![]()
Let ![]() and
and ![]() be the reflections of
be the reflections of ![]() in three lines which contains edges
in three lines which contains edges ![]() and
and ![]() respectively.
respectively.
![]() and
and ![]() are collinear. Respective line is known as the Steiner line of point
are collinear. Respective line is known as the Steiner line of point ![]() with respect to
with respect to ![]()
Proof
Let ![]() and
and ![]() be the foots of the perpendiculars dropped from
be the foots of the perpendiculars dropped from ![]() to lines
to lines ![]() and
and ![]() respectively.
respectively.
WLOG, Steiner line cross ![]() at
at ![]() and
and ![]() at
at ![]()
The line ![]() is Simson line of point
is Simson line of point ![]() with respect of
with respect of ![]()
![]() is midpoint of segment
is midpoint of segment ![]() homothety centered at
homothety centered at ![]() with ratio
with ratio ![]() sends point
sends point ![]() to a point
to a point ![]()
Similarly, this homothety sends point ![]() to a point
to a point ![]() , point
, point ![]() to a point
to a point ![]() therefore this homothety send Simson line to line
therefore this homothety send Simson line to line ![]()
Let ![]()
![]()
![]() is symmetric to
is symmetric to ![]()
Quadrangle ![]() is cyclic
is cyclic ![]()
![]() at point
at point ![]() Similarly, line
Similarly, line ![]() at
at ![]()
According the Collins Claim ![]() is
is ![]() therefore
therefore ![]()
Collings Clime
Let triangle ![]() be the triangle with the orthocenter
be the triangle with the orthocenter ![]() and circumcircle
and circumcircle ![]() Denote
Denote ![]() any line containing point
any line containing point ![]()
Let ![]() and
and ![]() be the reflections of
be the reflections of ![]() in the edges
in the edges ![]() and
and ![]() respectively.
respectively.
Prove that lines ![]() and
and ![]() are concurrent and the point of concurrence lies on
are concurrent and the point of concurrence lies on ![]()
Proof
Let ![]() and
and ![]() be the crosspoints of
be the crosspoints of ![]() with
with ![]() and
and ![]() respectively.
respectively.
WLOG ![]() Let
Let ![]() and
and ![]() be the points symmetric to
be the points symmetric to ![]() with respect
with respect ![]() and
and ![]() respectively.
respectively.
Therefore ![]()
![]()
![]()
Let ![]() be the crosspoint of
be the crosspoint of ![]() and
and ![]() is cyclic
is cyclic ![]()
Similarly ![]() is cyclic
is cyclic ![]() the crosspoint of
the crosspoint of ![]() and
and ![]() is point
is point ![]()
Usually the point ![]() is called the anti-Steiner point of the
is called the anti-Steiner point of the ![]() with respect to
with respect to ![]()
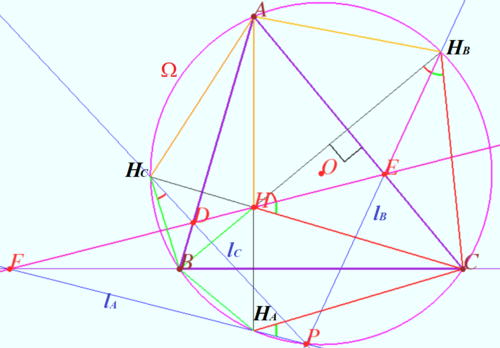
Ortholine
Let four lines made four triangles of a complete quadrilateral.
In the diagram these are ![]()
Let points ![]() and
and ![]() be the orthocenters of
be the orthocenters of ![]() and
and ![]() respectively.
respectively.
Prove that points ![]() and
and ![]() are collinear.
are collinear.
Proof
Let ![]() be Miquel point of a complete quadrilateral.
be Miquel point of a complete quadrilateral.
Line ![]() is the line which contain
is the line which contain ![]() Simson lines of
Simson lines of ![]() triangles.
triangles.
Using homothety centered at ![]() with ratio
with ratio ![]() we get
we get ![]() coinciding Stainer lines which contain points
coinciding Stainer lines which contain points ![]() and
and ![]() .
.
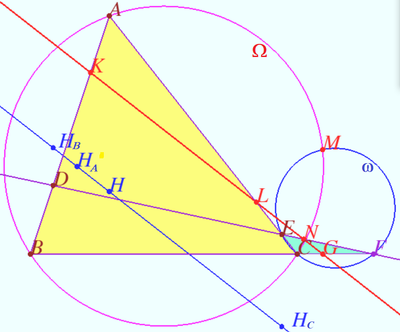
Proof 2
![]()
![]()
![]()
Points ![]() and
and ![]() are collinear.
are collinear.
According the Claim of parallel lines, points ![]() and
and ![]() are collinear.
are collinear.
Similarly points ![]() and
and ![]() are collinear as desired.
are collinear as desired.
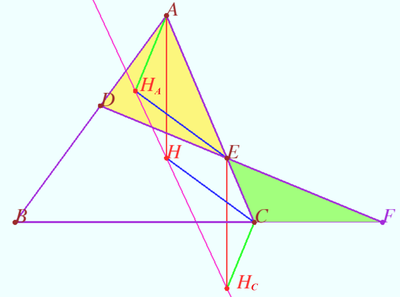
Claim of parallel lines
Let points ![]() and
and ![]() be collinear.
be collinear.
Let points ![]() be such that
be such that ![]()
Prove that points ![]() and
and ![]() are collinear.
are collinear.
Proof
Let ![]()
![]()
![]()
![]()
![]()
The segments ![]() and
and ![]() are corresponding segments in similar triangles.
Therefore
are corresponding segments in similar triangles.
Therefore ![]() and
and ![]() are collinear.
are collinear.
Shatunov-Tokarev line
Let the quadrilateral ![]() be given (
be given (![]() is not cyclic). Let points
is not cyclic). Let points ![]() and
and ![]() be the midpoints of
be the midpoints of ![]() and
and ![]() respectively. Let points
respectively. Let points ![]() and
and ![]() be such points that
be such points that ![]()
a) Prove that ![]()
b) Prove that the point ![]() lies on the line
lies on the line ![]() iff
iff ![]()
Proof
a) Let ![]() be the circle centered at
be the circle centered at ![]() with radius
with radius ![]() Let
Let ![]() be the circle centered at
be the circle centered at ![]() with radius
with radius ![]()
![]() is the median of
is the median of ![]()
The power of the point ![]() with respect to the circle
with respect to the circle ![]() is
is ![]()
![]() is the median of
is the median of ![]()
The power of the point ![]() with respect to the circle
with respect to the circle ![]() is
is ![]()
Therefore ![]() lies on the radical axis of
lies on the radical axis of ![]() and
and ![]() Similarly,
Similarly, ![]() lies on these line.
So the line
lies on these line.
So the line ![]() is the radical axes of
is the radical axes of ![]() and
and ![]()
This line is perpendicular to Gauss line ![]() which is the line of centers of two circles
which is the line of centers of two circles ![]() and
and ![]() as desired.
as desired.
b) ![]() is the median of
is the median of ![]()
![]() is the median of
is the median of ![]()
![]() lies on the radical axes of
lies on the radical axes of ![]() and
and ![]()
![]()
If the point ![]() satisfies the equation
satisfies the equation ![]() then locus of
then locus of ![]() is the straight line (one can prove it using method of coordinates).
is the straight line (one can prove it using method of coordinates).
The points ![]() and
and ![]() are satisfies this equation, so this line contain these points as desired.
are satisfies this equation, so this line contain these points as desired.
It is easy to understand that this line is parallel to Steiner line which is the radical axis of the circles centered at ![]() and
and ![]() with radii
with radii ![]() and
and ![]() respectively.
respectively.
Of course, it is parallel to Simson line.
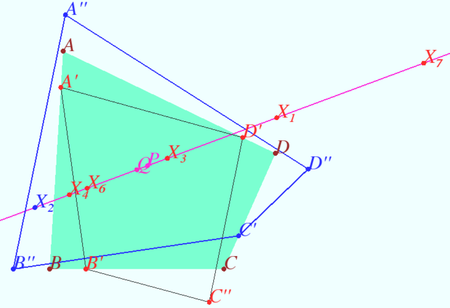
Shatunov-Tokarev concurrent lines
Let the quadrilateral ![]() be given (
be given (![]() is not cyclic).
is not cyclic).
Let points ![]() and
and ![]() be on the line
be on the line ![]() such that
such that ![]() . Similarly
. Similarly
![]()
![]()
![]()
Let points ![]() and
and ![]() be the crosspoints of the bisectors
be the crosspoints of the bisectors ![]()
Similarly points ![]() and
and ![]() are the crosspoints of the bisectors
are the crosspoints of the bisectors ![]()
Prove that lines ![]() and
and ![]() are concurrent.
are concurrent.
Proof
Segment ![]() is the median of the
is the median of the ![]()
Similarly ![]()
Let ![]() cross
cross ![]() at point
at point ![]()
We made simple calculations and get ![]() therefore point
therefore point ![]() lies on
lies on ![]() as desired.
as desired.
Shatunov point
Let the quadrilateral ![]() be given (
be given (![]() is not cyclic).
is not cyclic).
Let points ![]() and
and ![]() be on the lines
be on the lines ![]() and
and ![]() respectively such that
respectively such that ![]()
Let points ![]() and
and ![]() be on the segments
be on the segments ![]() and
and ![]() respectively such that
respectively such that ![]() where
where ![]()
Let points ![]() and
and ![]() be the crosspoints of the bisectors
be the crosspoints of the bisectors ![]()
Similarly points ![]() and
and ![]() are the crosspoints of the bisectors
are the crosspoints of the bisectors ![]()
Prove that lines ![]() and
and ![]() are concurrent.
are concurrent.
Proof
Segment ![]() is the cevian to the side AA' of the
is the cevian to the side AA' of the ![]()
We use the Stewart's theorem and get:
![]() Similarly
Similarly ![]()
![]()
![]() Let
Let ![]() cross
cross ![]() at point
at point ![]()
We made simple calculations and get ![]() therefore point
therefore point ![]() lies on
lies on ![]() as desired.
as desired.
Shatunov chain
Let the quadrilateral ![]() be given (
be given (![]() is not cyclic).
is not cyclic).
Let points ![]() and
and ![]() be on the line
be on the line ![]() such that
such that ![]() . Similarly
. Similarly ![]()
![]()
Let points ![]() and
and ![]() be the crosspoints of the bisectors
be the crosspoints of the bisectors ![]() and
and ![]()
We made quadrilateral ![]() using one point from the pare
using one point from the pare ![]() one point from the pare
one point from the pare ![]() one point from the pare
one point from the pare ![]() one point from the pare
one point from the pare ![]() For each quadrilateral we find the crosspoints of the bisectors
For each quadrilateral we find the crosspoints of the bisectors ![]() and
and ![]() and named these points as
and named these points as ![]()
Prove that lines ![]() cross line
cross line ![]() in 8 points and positions of these points are fixed for given
in 8 points and positions of these points are fixed for given ![]() (not depend from the length of
(not depend from the length of ![]()
Proof
The claim follows from the fact that there are ![]() combinations of quadrilateral vertices, and these 16 quadrilaterals are divided into pairs whose points of intersection with the line
combinations of quadrilateral vertices, and these 16 quadrilaterals are divided into pairs whose points of intersection with the line ![]() coincide.
coincide.
See Also
This article is a stub. Help us out by expanding it.