Pythagorean Theorem

The Pythagorean Theorem states that for a right triangle with legs of length $a$ and $b$ and hypotenuse of length $c$ we have the relationship ${a}^{2}+{b}^{2}={c}^{2}$ . This theorem has been know since antiquity and is a classic to prove; hundreds of proofs have been published and many can be demonstrated entirely visually(the book The Pythagorean Proposition alone consists of more than 370). The Pythagorean Theorem is one of the most frequently used theorems in geometry, and is one of the many tools in a good geometer's arsenal. A very large number of geometry problems can be solved by building right triangles and applying the Pythagorean Theorem.

This is generalized by the Pythagorean Inequality and the Law of Cosines.

Proofs

In these proofs, we will let $ABC$ be any right triangle with a right angle at ${} C$ .

Proof 1

We use $[ABC]$ to denote the area of triangle $ABC$ .

Let $H$ be the perpendicular to side $AB$ from ${} C$ .

$[asy] pair A, B, C, H; A = (0, 0); B = (4, 3); C = (4, 0); H = foot(C, A, B); draw(A--B--C--cycle); draw(C--H); draw(rightanglemark(A, C, B)); draw(rightanglemark(C, H, B)); label("$A$", A, SSW); label("$B$", B, ENE); label("$C$", C, SE); label("$H$", H, NNW); [/asy]$

Since $ABC, CBH, ACH$ are similar right triangles, and the areas of similar triangles are proportional to the squares of corresponding side lengths,

$\frac{[ABC]}{AB^2} = \frac{[CBH]}{CB^2} = \frac{[ACH]}{AC^2}$ .

But since triangle $ABC$ is composed of triangles $CBH$ and $ACH$ , $[ABC] = [CBH] + [ACH]$ , so $AB^2 = CB^2 + AC^2$ . Template:Halmos

Proof 2

Consider a circle $\omega$ with center $B$ and radius $BC$ . Since $BC$ and $AC$ are perpendicular, $AC$ is tangent to $\omega$ . Let the line $AB$ meet $\omega$ at $Y$ and $X$ , as shown in the diagram:

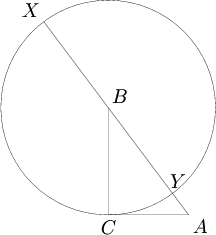
Evidently, $AY = AB - BC$ and $AX = AB + BC$ . By considering the power of point $A$ with respect to $\omega$ , we see

$AC^2 = AY \cdot AX = (AB-BC)(AB+BC) = AB^2 - BC^2$ . Template:Halmos

Proof 3

$ABCD$ and $EFGH$ are squares.

$[asy] pair A, B,C,D; A = (-10,10); B = (10,10); C = (10,-10); D = (-10,-10); pair E,F,G,H; E = (7,10); F = (10, -7); G = (-7, -10); H = (-10, 7); draw(A--B--C--D--cycle); label("$A$", A, NNW); label("$B$", B, ENE); label("$C$", C, ESE); label("$D$", D, SSW); draw(E--F--G--H--cycle); label("$E$", E, N); label("$F$", F,SE); label("$G$", G, S); label("$H$", H, W); label("a", A--B,N); label("a", B--F,SE); label("a", C--G,S); label("a", H--D,W); label("b", E--B,N); label("b", F--C,SE); label("b", G--D,S); label("b", A--H,W); label("c", E--H,NW); label("c", E--F); label("c", F--G,SE); label("c", G--H,SW); [/asy]$

$(a+b)^2=c^2+4\left(\frac{1}{2}ab\right)\implies a^2+2ab+b^2=c^2+2ab\implies a^2 + b^2=c^2$ . Template:Halmos

Proof 4

Take the derivative of $\omega_{\delta}(f)=\sup \{|f(x)-f(y)| \ | \ |x-y|\leq \delta, \ x\in I, \ y\in I\}$ , and because $\frac{dy}{dx}=\sqrt{\left(G+\frac{5}{144}+\frac{31\pi-70\ln2}{288}\right)\int_0^1f(x)\ln(1+x)dx},$ , $\omega_{\delta}(f)=\sup \{|f(x)-f(y)| \ | \ |x-y|\leq \delta, \ x\in I, \ y\in I\}$ , $\sqrt{\frac{143}{126}\int_{0}^{1}\frac{log\left(1+x\right)}{-x^{2}+2x+1}dx}=69$ . After a little bit of linear algebra and vector calculus, we have $\int_0^1 \frac{\tan^{-1}x}{\ln(1+x)} \ dx \int_0^1 f(x) \ln(1+x) \ dx=69^{69}$ , and we can do derivative and chain rule bash to get $I=\int_0^c\int_0^b\int_0^a\left(x^2+y^2\right)\sqrt{x^{\overset{\,}{2}}+y^2+z^2}{\rm\,d}x{\rm\,d}y{\rm\,d}z=69ab$ . From there, we can use barycentric coordinates to get that $ab=\int\limits_{0}^{+\infty }{\sin \left( \alpha x \right)\left( \psi \left( \frac{3}{4}+\beta x \right)-\psi \left( \frac{1}{4}+\beta x \right) \right)dx}$ , and after some complex bash and more barycentric coordinates, we arrive at the conclusion that $a^2+b^2=c^2$ .

- Stormerstyle

Common Pythagorean Triples

A Pythagorean Triple is a set of 3 positive integers such that $a^{2}+b^{2}=c^{2}$ , i.e. the 3 numbers can be the lengths of the sides of a right triangle. Among these, the Primitive Pythagorean Triples, those in which the three numbers have no common divisor, are most interesting. A few of them are: