8. Lists and Tuples

A list or a tuple is an ordered collection of values. The values that make up a list or tuple are called its elements, or its items. We will use the term element or item to mean the same thing. Lists and tuples are similar to strings, which are ordered collections of characters, except that the elements of a list can be of any type. Lists, tuples, and strings — and other collections that maintain the order of their items — are called sequences.

We’ve already seen lists in previous chapters, so we’ll start by looking at tuples.

8.1. Tuples are used for grouping data

We can group together pairs of values by surrounding with parentheses. For example:

year_born = ("Isaac Newton", 1642)

This is an example of a data structure — a mechanism for grouping and organizing data to make it easier to use.

The pair is an example of a tuple. Generalizing this, a tuple can be used to group any number of items into a single compound value. Syntactically, a tuple is a comma-separated sequence of values. Although it is not necessary, it is conventional to enclose tuples in parentheses:

julia = ("Julia", "Roberts", 1967, "Duplicity", 2009, "Actress", "Atlanta, Georgia")

Tuples are useful for representing what other languages often call records — some related information that belongs together, like your student record. There is no description of what each of these fields means, but we can guess. A tuple lets us “chunk” together related information and use it as a single thing.

Tuples support the same sequence operations as strings. The index operator selects an element from a tuple.

julia = ("Julia", "Roberts", 1967, "Duplicity", 2009, "Actress", "Atlanta, Georgia")
print(julia[2])

But if we try to use item assignment to modify one of the elements of the tuple, we get an error:

julia = ("Julia", "Roberts", 1967, "Duplicity", 2009, "Actress", "Atlanta, Georgia")
julia[0] = "X"

So like strings, tuples are immutable. Once Python has created a tuple in memory, it cannot be changed.

Of course, even if we can’t modify the elements of a tuple, we can always make the julia variable reference a new tuple holding different information. To construct the new tuple, it is convenient that we can slice parts of the old tuple and join up the bits to make the new tuple. So if julia has a new recent film, we could change her variable to reference a new tuple that used some information from the old one:

julia = ("Julia", "Roberts", 1967, "Duplicity", 2009, "Actress", "Atlanta, Georgia")
julia = julia[:3] + ("Eat Pray Love", 2010) + julia[5:]
print(julia)

To create a tuple with a single element (but you’re probably not likely to do that too often), we have to include the final comma, because without the final comma, Python treats the (5) below as an integer in parentheses:

>>> tup = (5,)
>>> type(tup)
<class 'tuple'>
>>> x = (5)
>>> type(x)
<class 'int'>

8.2. Tuple assignment

Python has a very powerful tuple assignment feature that allows a tuple of variables on the left of an assignment to be assigned values from a tuple on the right of the assignment.

julia = ("Julia", "Roberts", 1967, "Duplicity", 2009, "Actress", "Atlanta, Georgia")
(name, surname, bYear, movie, mYear, profession, birthplace) = julia

print(name)
print(surname)
print(bYear)
print(movie)
print(mYear)
print(profession)
print(birthplace)

This does the equivalent of seven assignment statements, all on one easy line. One requirement is that the number of variables on the left must match the number of elements in the tuple.

One way to think of tuple assignment is as tuple packing/unpacking. In tuple packing, the values are ‘packed’ together in a tuple. In tuple unpacking, the values in a tuple are ‘unpacked’ into individual variables.

b = ("Bob", 19, "CS")       # tuple packing
(name, age, studies) = b    # tuple unpacking

print(name)
print(age)
print(studies)

Once in a while, it is useful to swap the values of two variables. With conventional assignment statements, we have to use a temporary variable. For example, to swap a and b:

a = 3
b = 5

# use a temporary variable to swap the values of a and b
temp = a
a = b
b = temp

print("a="+str(a)+" b="+str(b))

Tuple assignment solves this problem neatly:

a = 3
b = 5

# swap using tuples
(a,b) = (b,a)

print("a="+str(a)+" b="+str(b))

The left side is a tuple of variables; the right side is a tuple of values. Each value is assigned to its respective variable. All the expressions on the right side are evaluated before any of the assignments. This feature makes tuple assignment quite versatile.

Naturally, the number of variables on the left and the number of values on the right have to be the same — if you try to run the code below, you’ll get an error:

(a,b,c,d) = (1,2,3)

8.3. Tuples as return values

Functions can always only return a single value, but by making that value a tuple, we can effectively group together as many values as we like, and return them together. This is very useful — we often want to know some batsman’s highest and lowest score, or we want to find the mean and the standard deviation, or we want to know the year, the month, and the day, or if we’re doing some some ecological modeling we may want to know the number of rabbits and the number of wolves on an island at a given time.

For example, we could write a function that returns both the area and the circumference of a circle of radius r:

import math

def circum_area(r):
    """ Return (circumference, area) of a circle of radius r """
    c = 2 * math.pi * r
    a = math.pi * r * r
    return (c, a)

print(circum_area(10))

8.4. List and Tuple values

There are several ways to create a new list; the simplest is to enclose the elements in square brackets ([ and ]):

ps = [10, 20, 30, 40]
qs = ["spam", "bungee", "swallow"]

The first example is a list of four integers. The second is a list of three strings. The elements of a list don’t have to be the same type. The following list contains a string, a float, an integer, and (amazingly) another list:

zs = ["hello", 2.0, 5, [10, 20]]

A list within another list is said to be nested.

Finally, a list with no elements is called an empty list, and is denoted [].

We can do more complicated things too. For example, we can make a list of tuples, where one of the items in the tuple is itself a list:

students = [
  ("John", ["CompSci", "Physics"]),
  ("Vusi", ["Maths", "CompSci", "Stats"]),
  ("Jess", ["CompSci", "Accounting", "Economics", "Management"]),
  ("Sarah", ["InfSys", "Accounting", "Economics", "CommLaw"]),
  ("Zuki", ["Sociology", "Economics", "Law", "Stats", "Music"])]

Tuples items can themselves be other tuples. For example, we could improve the information about our movie stars to hold the full date of birth rather than just the year, and we could have a list of some of her movies and dates that they were made, and so on:

julia_more_info = ( ("Julia", "Roberts"), (8, "October", 1967),
                    "Actress", ("Atlanta", "Georgia"),
                    [ ("Duplicity", 2009),
                      ("Notting Hill", 1999),
                      ("Pretty Woman", 1990),
                      ("Erin Brockovich", 2000),
                      ("Eat Pray Love", 2010),
                      ("Mona Lisa Smile", 2003),
                      ("Oceans Twelve", 2004) ])

Notice in this case that the tuple has just five elements — but each of those in turn can be another tuple, a list, a string, or any other kind of Python value. This property is known as being heterogeneous, meaning that it can be composed of elements of different types.

8.5. Accessing elements

The syntax for accessing the elements of a list is the same as the syntax for accessing the characters of a string or a tuple — the index operator: [] (not to be confused with an empty list). The expression inside the brackets specifies the index. Remember that the indices start at 0:

numbers = [17, 5]
a = numbers[0]
print(a)

Any expression evaluating to an integer can be used as an index:

numbers = [17, 5]
b = numbers[9-8]
print(b)

If you try to access or assign to an element that does not exist, you get a runtime error:

numbers = [17, 5]
d = numbers[2]    # will give an error
print(d)

It is common to use a loop variable as a list index.

horsemen = ["war", "famine", "pestilence", "death"]

for i in [0, 1, 2, 3]:
    print(horsemen[i])

Each time through the loop, the variable i is used as an index into the list, printing the i‘th element. This pattern of computation is called a list traversal.

The above sample doesn’t need or use the index i for anything besides getting the items from the list, so this more direct version — where the for loop gets the items — might be preferred:

horsemen = ["war", "famine", "pestilence", "death"]

for h in horsemen:
    print(h)

The function len returns the length of a list, which is equal to the number of its elements. If you are going to use an integer index to access the list, it is a good idea to use this value as the upper bound of a loop instead of a constant. That way, if the size of the list changes, you won’t have to go through the program changing all the loops; they will work correctly for any size list:

horsemen = ["war", "famine", "pestilence", "death"]

for i in range(len(horsemen)):
    print(horsemen[i])

The last time the body of the loop is executed, i is len(horsemen) - 1, which is the index of the last element. (But the version without the index looks even better now!)

Although a list can contain another list, the nested list still counts as a single element in its parent list. The length of this list is 4:

print(len(["car makers", 1, ["Ford", "Toyota", "BMW"], [1, 2, 3]]))

in and not in are Boolean operators that test membership in a sequence. We used them previously with strings, but they also work with lists and other sequences:

horsemen = ["war", "famine", "pestilence", "death"]
print("pestilence" in horsemen)  # True
print("debauchery" in horsemen)  # False
print("debauchery" not in horsemen)   # True

8.6. List operations

The + operator concatenates lists:

a = [1, 2, 3]
b = [4, 5, 6]
c = a + b
print(c)

Similarly, the * operator repeats a list a given number of times:

a = [0]
b = [0] * 4
print(b)
c = [1, 2, 3] * 3
print(c)

The first example repeats [0] four times. The second example repeats the list [1, 2, 3] three times.

The slice operations we saw previously with strings let us work with sublists:

aList = ["a", "b", "c", "d", "e", "f"]
print(aList[1:3])
print(aList[:4])
print(aList[3:])
print(aList[:])

8.7. Lists are mutable

Unlike strings and tuples, lists are mutable, which means we can change their elements. Using the index operator on the left side of an assignment, we can update one of the elements:

fruit = ["banana", "apple", "quince"]
fruit[0] = "pear"
fruit[2] = "orange"
print(fruit)

The bracket operator applied to a list can appear anywhere in an expression. When it appears on the left side of an assignment, it changes one of the elements in the list, so the first element of fruit has been changed from "banana" to "pear", and the last from "quince" to "orange". An assignment to an element of a list is called item assignment. Item assignment does not work for strings:

myString = "TEST"
myString[2] = "X"
print(myString)

but it does for lists:

myList = ["T", "E", "S", "T"]
myList[2] = "X"
print(myList)

With the slice operator we can update a whole sublist at once:

aList = ["a", "b", "c", "d", "e", "f"]
aList[1:3] = ["x", "y"]
print(aList)

We can also remove elements from a list by assigning an empty list to them:

aList = ["a", "b", "c", "d", "e", "f"]
aList[1:3] = []
print(aList)

And we can add elements to a list by squeezing them into an empty slice at the desired location:

aList = ["a", "d", "f"]
aList[1:1] = ["b", "c"]
print(aList)
aList[4:4] = ["e"]
print(aList)

Using slices to delete list elements can be error-prone. Python provides an alternative that is more readable. The del statement removes an element from a list:

a = ["one", "two", "three"]
del a[1]
print(a)

As you might expect, del causes a runtime error if the index is out of range.

You can also use del with a slice to delete a sublist:

aList = ["a", "b", "c", "d", "e", "f"]
del aList[1:5]
print(aList)

As usual, the sublist selected by slice contains all the elements up to, but not including, the second index.

8.8. Objects and references

After we execute these assignment statements

a = "banana"
b = "banana"

we know that a and b will refer to a string object with the letters "banana". But we don’t know yet whether they point to the same string object.

There are two possible ways the Python interpreter could arrange its memory:

In one case, a and b refer to two different objects that have the same value. In the second case, they refer to the same object.

We can test whether two names refer to the same object using the is operator:

a = "banana"
b = "banana"
print(a is b)

This tells us that both a and b refer to the same object, and that it is the second of the two state snapshots that accurately describes the relationship.

Since strings are immutable, Python optimizes resources by making two names that refer to the same string value refer to the same object.

This is not the case with lists:

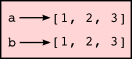
a = [1, 2, 3]
b = [1, 2, 3]
print("Do they look the same? " + str(a==b))
print("Are they the same? " + str(a is b))

The state snapshot here looks like this:

a and b have the same value but do not refer to the same object.

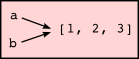
Since variables refer to objects, if we assign one variable to another, both variables refer to the same object:

a = [1, 2, 3]
b = a
print("Do they look the same? " + str(a==b))
print("Are they the same? " + str(a is b))

In this case, the state snapshot looks like this:

Because the same list has two different names, a and b, we say that it is aliased. Changes made with one alias affect the other:

a = [1, 2, 3]
b = a
b[0] = 5
print(a)   # changing b also changes a, since a and b are the same list

Although this behavior can be useful, it is sometimes unexpected or undesirable. In general, it is safer to avoid aliasing when you are working with mutable objects (i.e. lists at this point in our textbook, but we’ll meet more mutable objects as we cover classes and objects, dictionaries and sets). Of course, for immutable objects (i.e. strings, tuples), there’s no problem — it is just not possible to change something and get a surprise when you access an alias name. That’s why Python is free to alias strings (and any other immutable kinds of data) when it sees an opportunity to economize.

If we want to modify a list and also keep a copy of the original, we need to be able to make a copy of the list itself, not just the reference. This process is sometimes called cloning, to avoid the ambiguity of the word copy.

The easiest way to clone a list is to use the slice operator:

a = [1, 2, 3]
b = a[:]
print("a is "+str(a)+" and b is "+str(b))
print("Do they look the same? " + str(a==b))
print("Are they the same? " + str(a is b))

Taking any slice of a creates a new list. In this case the slice happens to consist of the whole list. So now the relationship is like this:

Now we are free to make changes to b without worrying that we’ll inadvertently be changing a:

a = [1, 2, 3]
b = a[:]
print("a is "+str(a)+" and b is "+str(b))
b[0] = 5
print("a is "+str(a)+" and b is "+str(b))

8.9. Lists and `for` loops

The for loop also works with lists, as we’ve already seen. The generalized syntax of a for loop is:

for VARIABLE in LIST:
    BODY

So, as we’ve seen

friends = ["Joe", "Zoe", "Brad", "Angelina", "Zuki", "Thandi", "Paris"]
for friend in friends:
    print(friend)

It almost reads like English: For (every) friend in (the list of) friends, print (the name of the) friend.

Any list expression can be used in a for loop:

for number in range(20):
    if number % 3 == 0:
        print(number)

for fruit in ["banana", "apple", "quince"]:
    print("I like to eat " + fruit + "s!")

The first example prints all the multiples of 3 between 0 and 19. The second example expresses enthusiasm for various fruits.

Since lists are mutable, we often want to traverse a list, changing each of its elements. The following squares all the numbers in the list xs:

xs = [1, 2, 3, 4, 5]
for i in range(len(xs)):
    xs[i] = xs[i]**2
print(xs)

Take a moment to think about range(len(xs)) until you understand how it works.

Sometimes we are interested in both the value of an item (we want to square that value) and its index (so that we can assign the new value to that position). This pattern is common enough that Python provides a nicer way to implement it: enumerate generates pairs of both (index, value) during the list traversal. Try this next example to see more clearly how enumerate works:

for (i, v) in enumerate(["banana", "apple", "pear", "lemon"]):
    print(str(i)+" "+str(v))

8.10. List methods

The dot operator can also be used to access built-in methods of list objects. We’ll start with the most useful method for adding something onto the end of an existing list:

mylist = []
mylist.append(5)   # add 5 to list
print(mylist)
mylist.append(27)  # add 27 to list
print(mylist)
mylist.append(3)   # add 3 and 12 to list
mylist.append(12)
print(mylist)

append is a list method which adds the argument passed to it to the end of the list. We’ll use it heavily when we’re creating new lists. Continuing with this example, we show several other list methods:

mylist = []
mylist.append(5)   # add 5 to list
print(mylist)
mylist.append(27)  # add 27 to list
print(mylist)
mylist.append(3)   # add 3 and 12 to list
mylist.append(12)
print(mylist)
print("Insert a 12 in position 1")
mylist.insert(1, 12)
print(mylist)
print("Count the number of 12s in the list")
print(mylist.count(12))
print("Add an entire list onto the end of the list")
mylist.extend([5, 9, 5, 11])   # Put whole list onto end of mylist
print(mylist)
print("Find the first index of 9 in the list")
print(mylist.index(9))   # Find index of first 9 in mylist
print("Reverse the list")
mylist.reverse()
print(mylist)
print("Sort the list")
mylist.sort()
print(mylist)
print("Remove the first 12 from the list")
mylist.remove(12)             # Remove the first 12 in the list
print(mylist)

Experiment and play with the list methods shown here, and read their documentation until you feel confident that you understand how they work.

8.11. List parameters

Passing a list as an argument actually passes a reference to the list, not a copy or clone of the list. So parameter passing creates an alias for you: the caller has one variable referencing the list, and the called function has an alias (a new variable pointing to the same list), but there is only one underlying list object.

For example, the function below takes a list as an argument and multiplies each element in the list by 2:

def double_stuff(a_list):
    """ Overwrite each element in a_list with double its value. """
    for (idx, val) in enumerate(a_list):
        a_list[idx] = 2 * val

things = [2, 5, 9]
double_stuff(things)
print(things)

In the function above, the parameter a_list and the variable things are aliases for the same object. So before any changes to the elements in the list, the state snapshot looks like this:

If a function modifies the items of a list parameter, the caller sees the change.

Functions which take lists as arguments and change them during execution are called modifiers and the changes they make are called side effects.

A pure function does not produce side effects. It communicates with the calling program only through parameters, which it does not modify, and a return value. Here is double_stuff written as a pure function:

def double_stuff(a_list):
    """ Return a new list which contains
        doubles of the elements in a_list.
    """
    newList = []    # create an empty list to store the result
    for value in a_list:
        # append double the entry in a_list to newList
        newElem = 2 * value
        newList.append(newElem)
    return newList

things = [2, 5, 9]
xs = double_stuff(things)
print("things: "+str(things))   # things is unchanged
print("xs: "+str(xs))

Notice that this version of double_stuff does not change its arguments:

An early rule we saw for assignment said “first evaluate the right hand side, then assign the resulting value to the variable”. So it is quite safe to assign the function result to the same variable that was passed to the function:

def double_stuff(a_list):
    """ Return a new list which contains
        doubles of the elements in a_list.
    """
    newList = []    # create an empty list to store the result
    for value in a_list:
        # append double the entry in a_list to newList
        newElem = 2 * value
        newList.append(newElem)
    return newList

things = [2, 5, 9]
things = double_stuff(things)
print(things)

Which style is better?

Anything that can be done with modifiers can also be done with pure functions. In fact, some programming languages only allow pure functions. There is some evidence that programs that use pure functions are faster to develop and less error-prone than programs that use modifiers. Nevertheless, modifiers are convenient at times, and in some cases, functional programs are less efficient.

In general, we recommend that you write pure functions whenever it is reasonable to do so and resort to modifiers only if there is a compelling advantage. This approach might be called a functional programming style.

The pure version of double_stuff above made use of an important pattern for your toolbox. Whenever you need to write a function that creates and returns a list, the pattern is usually:

initialize a result variable to be an empty list
loop
   create a new element
   append it to result
return the result

8.12. Strings and lists

Two of the most useful methods on strings involve conversion to and from lists of substrings. The split method (which we’ve already seen) breaks a string into a list of words. By default, any number of whitespace characters is considered a word boundary:

song = "The rain in Spain..."
wds = song.split()
print(wds)

An optional argument called a delimiter can be used to specify which string to use as the boundary marker between substrings. The following example uses the string ai as the delimiter:

song = "The rain in Spain..."
wds = song.split("ai")
print(wds)

Notice that the delimiter doesn’t appear in the result.

The inverse of the split method is join. You choose a desired separator string, (often called the glue) and join the list with the glue between each of the elements:

wds = ['The', 'rain', 'in', 'Spain...']
glue = ';'
s = glue.join(wds)
print(s)

The list that you glue together (wds in this example) is not modified. Also, as these next examples show, you can use empty glue or multi-character strings as glue:

wds = ['The', 'rain', 'in', 'Spain...']
glue1 = ' '
s1 = glue1.join(wds)
print(s1)
glue2 = ' --- '
s2 = glue2.join(wds)
print(s2)
glue3 = ''
s3 = glue3.join(wds)
print(s3)

Python has a built-in type conversion function called list that tries to turn whatever you give it into a list.

xs = list("Crunchy Frog")
print(xs)
phrase = "".join(xs)
print(phrase)

8.13. Nested lists

A nested list is a list that appears as an element in another list. In this list, the element with index 3 is a nested list:

nested = ["hello", 2.0, 5, [10, 20]]

If we output the element at index 3, we get:

nested = ["hello", 2.0, 5, [10, 20]]
print(nested[3])

To extract an element from the nested list, we can proceed in two steps:

nested = ["hello", 2.0, 5, [10, 20]]
elem = nested[3]
print(elem[1])

Or we can combine them:

nested = ["hello", 2.0, 5, [10, 20]]
print(nested[3][1])

Bracket operators evaluate from left to right, so this expression gets the 3’th element of nested and extracts the 1’th element from it.

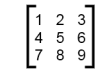
Nested lists are often used to represent matrices. For example, the matrix:

might be represented as:

mx = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

mx is a list with three elements, where each element is a row of the matrix. We can select an entire row from the matrix in the usual way:

mx = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
print(mx[1])

Or we can extract a single element from the matrix using the double-index form:

mx = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
print(mx[1][2])

The first index selects the row, and the second index selects the column. Although this way of representing matrices is common, it is not the only possibility. A small variation is to use a list of columns instead of a list of rows. Later we will see a more radical alternative using a dictionary.

8.14. Glossary

aliases: Multiple variables that contain references to the same object.
clone: To create a new object that has the same value as an existing object. Copying a reference to an object creates an alias but doesn’t clone the object.
data structure: An organization of data for the purpose of making it easier to use.
delimiter: A character or string used to indicate where a string should be split.
element: One of the values in a list (or other sequence). The bracket operator selects elements of a list. Also called item.
immutable data value: A data value which cannot be modified. Assignments to elements or slices (sub-parts) of immutable values cause a runtime error.
index: An integer value that indicates the position of an item in a list. Indexes start from 0.
item: See element.
list: A collection of values, each in a fixed position within the list. Like other types str, int, float, etc. there is also a list type-converter function that tries to turn whatever argument you give it into a list.
list traversal: The sequential accessing of each element in a list.
modifier: A function which changes its arguments inside the function body. Only mutable types can be changed by modifiers.
mutable data value: A data value which can be modified. The types of all mutable values are compound types. Lists and dictionaries are mutable; strings and tuples are not.
nested list: A list that is an element of another list.
object: A thing to which a variable can refer.
pattern: A sequence of statements, or a style of coding something that has general applicability in a number of different situations. Part of becoming a mature Computer Scientist is to learn and establish the patterns and algorithms that form your toolkit. Patterns often correspond to your “mental chunking”.
promise: An object that promises to do some work or deliver some values if they’re eventually needed, but it lazily puts off doing the work immediately. Calling range produces a promise.
pure function: A function which has no side effects. Pure functions only make changes to the calling program through their return values.
sequence: Any of the data types that consist of an ordered collection of elements, with each element identified by an index.
side effect: A change in the state of a program made by calling a function. Side effects can only be produced by modifiers.
step size: The interval between successive elements of a linear sequence. The third (and optional argument) to the range function is called the step size. If not specified, it defaults to 1.
tuple: An immutable data value that contains related elements. Tuples are used to group together related data, such as a person’s name, their age, and their gender.
tuple assignment: An assignment to all of the elements in a tuple using a single assignment statement. Tuple assignment occurs simultaneously rather than in sequence, making it useful for swapping values.

Navigation