 by raxu, Jun 26, 2015, 2:01 AM
by raxu, Jun 26, 2015, 2:01 AM
Let ABC be a scalene triangle. Let
 ,
, 
and

be the respective intersections with BC of the internal angle bisector, external angle bisector, and the median from A. The circumcircle of

intersects

a second time at point

different from A. Define

and

analogously. Prove that the circumcenter of

lies on the Euler line of ABC.
(The Euler line of ABC is the line passing through the circumcenter, centroid, and orthocenter of ABC.)
Proposed by Ivan BorsencoThis post has been edited 2 times. Last edited by v_Enhance, Aug 23, 2016, 12:45 AM
Reason: Add author
 by Entei, Jun 6, 2025, 8:40 PM
by Entei, Jun 6, 2025, 8:40 PM 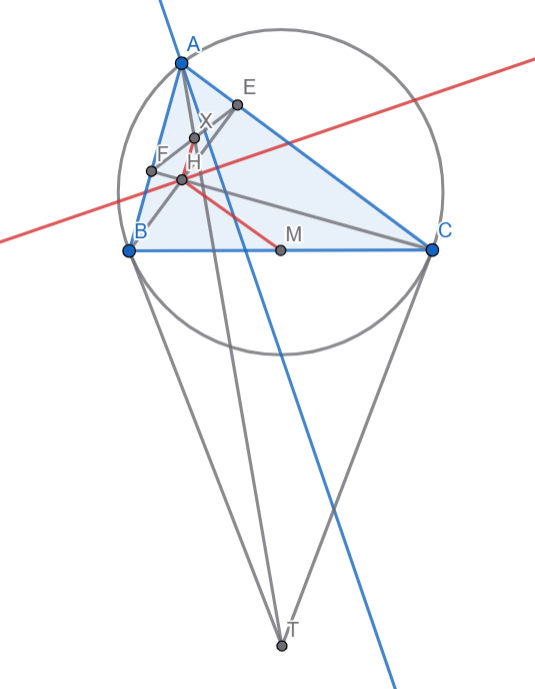
 July 2017
July 2017
 December 2016
December 2016